Engineering Mechanics

LESSON 24.

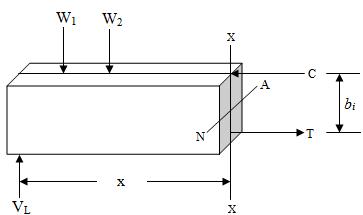
(B)

 

(C)

Fig.24.1

Bending equation gives  or \[{M \over {I}} = {{{f_{all}}} \over {{y_{max}}}}\]  or M = \[{I \over {{y_{max}}}}\] fall

M_R = Z f_max

This  quantity "ZF" is termed as "Moment of Resistence", which totally depends on allowable stress fall ans section modules Z.

• It does not depend on the system of loading.
  

• However, it would be necessary that moment of resistence is always greater than or equal to the external bending moment.
  

24.2 SECTION MODULUS

It is a property of sectional area.

We know that  \[{M \over {I}} = {f \over y}\]

Or f = \[{M \over {I/y}}\]  and f_max = \[{M \over {I/{y_{max}}}}\]

Where \[{I \over {{y_{max}}}}\]  is called section modulus ‘Z’.

Therefore  Z =  \[{I \over {{y_{max}}}}\]

f_max = \[{M \over Z}\]   which is similar to f =  \[{P \over A}\]    (in simple tension and compression)

• For same area of cross-section, but with different shapes, the section modulus will be different.

• In bending it would be desirable to choose sections which give the maximum value of section modulus.

• I sections have been found to give the maximum section modulus for a specific area of cross-section and hence should be preferred for bending loads.

7.8 SECTION MODULUS FOR VARIOUS SHAPES OF BEAM SECTIONS

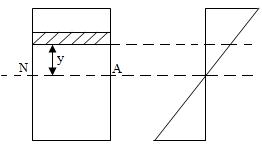
(i) Rectangular Section

Fig.24.2 shows a rectangular section of width b and depth d. Let the horizontal centroidal axis be the neutral axis.

 

Fig.24.2

Section Modulus = Z = \[{{Moment of inertia about the neutral axis} \over {Distance of most distant point from the neutral axis}}\]

 =  \[{I \over {{y{max}}}}\]

I =  \[{{b{d^3}} \over {12}}\]  and y_max =  \[{d \over 2}\]

Z = \[{{b{d^3}} \over {12}}\]  . \[{2 \over d}\]  = \[{{b{d^2}} \over {6}}\]

Let f be the maximum stress offered by the beam section.

Therefore moment of resistance = M = f Z = f  \[{{b{d^2}} \over {6}}\]

Or M =  \[{1 \over 6}\]  f bd²

(ii) Hollow Rectangular Section

Fig.24.3 shows a hollow rectangular section. Let the overall width and depth be B and D. Let the width and depth of the centrally situated rectangular hole be b and d.

 

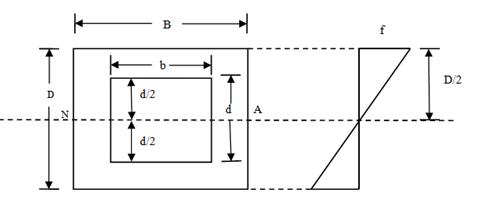
Fig.24.3

Moment of inertia about the neutral axis = I =  \[{{B{D^3}} \over {12}}\]  -  \[{{b{d^3}} \over {12}}\]  =   \[{1 \over 12}\]  [BD³ - bd³]
y_max =   \[{D \over 2}\]

Therefore, Section Modulus = Z = \[{I \over {{y_{max}}}}={1 \over {12}}(B{D^3}-b{d^3}\] )  \[{2 \over D}\]

Z = \[{{B{D^3} - b{d^3}} \over {6D}}\]

If f be the maximum bending stress the moment of resistance = M = f Z

M =  \[{1 \over 6}f\left( {{{B{D^3} - b{d^3}} \over D}} \right)\]

(iii) Circular Section

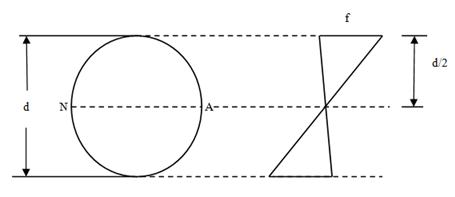
 Fig. 24.4

Let the diameter of the section be d. Moment of inertia of the section about the neutral axis = I =  \[{{\pi{d^4}} \over {64}}\]

y_max = \[{d \over 2}\]

Section Modulus = Z =  \[{I \over {{y_{max}}}}\]  = \[{{\pi{d^3}} \over {32}}\]

If  f be the stress offered by the section, the moment of resistance = M = f Z

    = f  \[{{\pi{d^3}} \over {32}}\]

(iv) Hollow Circular Section

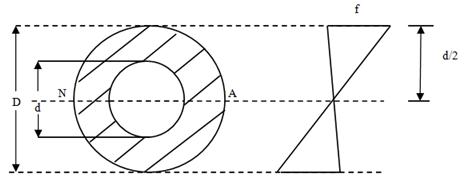
Fig.24.5

Fig.24.5 shows a hollow circular section of external diameter D and internal diameter d.

Moment of inertia about the neutral axis = I =  \[{\pi\over {64}}\left[ {{D^4} - {d^4}} \right]\]

y_max = \[{D \over 2}\]

Therefore, section modulus = Z = \[{I \over {{y_{max}}}}\]   =  \[{{\pi \left({{D^4} - {d^4}} \right)} \over {32D}}\]

If f be the maximum stress offered by the section, the moment of resistance = M = f Z

M = f   \[{{\pi \left({{D^4} - {d^4}} \right)} \over {32D}}\]

Example 24.1: Fig.24.6 shows the section of a tube of aluminium alloy. Determine the maximum moment that can be applied to the tube if the permissible bending stress is 100 N/mm². Find also the radius of curvature of the tube as it bends. Take E = 72800 N/mm².

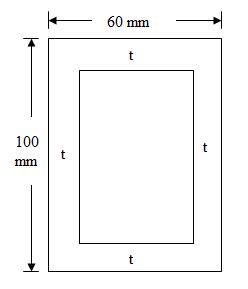
Fig.24.6

 

Solution: Moment of Inertia of the section,

I = \[{{60 \times {{100}^3}} \over {12}} - {{50 \times {{90}^3}} \over {12}} = 1962500\]

 = 1962500 mm⁴

Maximum moment on the section, M = \[{f \over {{y_{max}}}}.I = {{100 \times 1962500} \over {50}}\] Nmm

= 3925000 Nmm

Radius of Curvature, R =  \[{{EI} \over M} = {{72800 \times 1962500} \over {3925000}}\]  mm

= 36400 mm

Example 24.2: A cast iron test beam 25mm × 25mm in section and 2 m long and supported at the ends fails when a central load of 700N is applied. What uniformly distributed load will break a cantilever of the same material 55mm wide, 110mm deep and 3m long?

Solution: Let us first consider the test beam.

Maximum bending moment = M = \[{{WL}\over 4}={{700\times 2}\over 4}\times 1000Nmm\]   = 35 × 10⁴ Nmm

Moment of Resistance, R = \[{1 \over 6}.fb{d^2}\]  = \[{1 \over 6}.f \times 25 \times {25^2}\] =  \[{{15625} \over 6}f = 2604.17fNmm\]

 

 Fig.24.7

Equating the moment of resistance to the maximum bending moment

\[2604.17f=\]   35 × 10⁴

f = \[{{35{\rm{}} \times {\rm{}}{{10}^4}{\rm{}}} \over {2604.17}}\]  = 134.39 N/mm²

Now let us consider the cantilever.

Let the distributed load on the cantilever be w N/m run so as to break it.

Therefore, maximum bending moment = M =  \[{{w{l^2}} \over 2} = {{w \times {3^2}} \over 2} \times 1000Nmm\]  = 4500w N mm

Moment of Resistance of the section =  \[{1 \over 6}.fb{d^2} = {1 \over 6} \times 134.39 \times 55 \times {110^2}Nmm\]

 = 14.91 × 10⁶ N mm

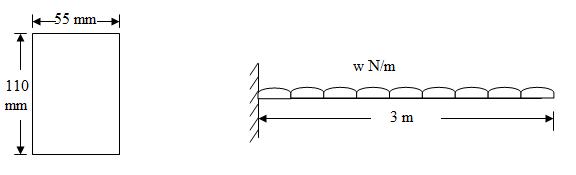
Fig.24.8

Equating the maximum bending moment to moment of resistance we have,

4500 w =14.91 × 10⁶

w= 3313 N/m

Example 24.3: A machine component of semi circular section 300mm diameter acts as a beam of span 1.50m. It is placed with its base horizontal. If it carries a uniformly distributed load of 150kN/m run on the whole span, find the maximum stress induced.

Solution: Moment of inertia of the section about the neutral axis = I = 0.00686 d⁴

Extreme fibre distance from the neutral axis = r -  \[{{4r} \over {3\Pi }} = {{3\Pi- 4} \over {4\Pi }} \times r = 0.5756\]

r = 0.2878 d

Section modulus, Z =  \[{{0.00686{d^4}} \over {0.2878d}} = 0.0238{d^3}\]

Maximum bending moment, M =  \[{{300 \times {{1.50}^2}} \over 8} = 84.375kNm\]

Maximum bending stress  \[{f_{max}}={M \over Z}={{84.375\times{{10}^6}}\over{0.0238\times{{300}^3}}}=131.30\]  N/mm²

Example 24.4: Find the safe concentrated load that can be applied at the free end of a 2m long cantilever. The section of the cantilever is a hollow square of external side 50mm and internal side 40mm the safe bending stress for the material being 65 N/mm².

Solution: Moment of inertia of the section of the cantilever,

I = \[{{{{50}^4}} \over {12}}-{{{{40}^4}} \over {12}}=307500\]  mm⁴

Section modulus, Z = \[{I \over {{y_{max}}}}={{307500} \over {30}}\]   = 10250 mm³

Let the safe concentrated load at the free end be W Newton

Maximum B.M, M = W × 2 × 1000 = 2000 W Nmm

M = f Z, 2000 W = 65 × 10250

W   = \[{{65 \times 10250} \over {2000}}=\]  333.125 N

Example 24.5: The moment of inertia of a beam section 450mm deep is 60.5 × 10⁷ mm⁴. Find the span over which a beam of this section, when simply supported, could carry a uniformly distributed load of 45kN per meter run. The flange stress in the material is not to exceed 110 N/mm².

Solution: Section modulus of section = Z =  \[{I \over {{y_{max}}}} = {{60.5 \times {{10}^7}} \over {250}}\]

Therefore, Z = 24.2 × 10⁵ mm³

Let the maximum span be l meter.

Therefore, maximum bending moment = M = \[{{w{l^2}} \over 8}={{45000\times{l^2}} \over 8} \times 1000Nmm\]

= 56.25 × 10⁵ l² N mm

Moment of resistance of the section corresponding to the maximum bending stress of 110 N/mm²

= f Z = 110 × 24.2 × 10⁵ N mm

Equating the maximum bending moment to the moment of resistance, we get

56.25 × 10⁵ l² = 110 × 24.2 × 10⁵

l² =  \[{{110\times 24.2\times{{10}^5}} \over {56.25\times{{10}^5}}}=47.32\]

Therefore, l = 6.88 m, say 7 m