LESSON 20. Design of Gear Pump

20.1 Introduction

Most of the hydraulic systems are generally provided with positive displacement pumps. In these pumps there is hardly any slippage and the quantity of fluid pumped is nearly same for each rotation of shaft. Specially piston pumps exhibit this quality. The piston sucks and pushes the same quantity (volume) of fluid every rotation of shaft.

20.2 Design of Gear Pump

Therefore,

                                                            Q         =          V x N

            Where,                                     Q         =          Flow rate

                                                            V         =          Displacement 

                                                            N         =          speed

In actual practice there may be some leakages because of mating components are not perfect fits and therefore, the leakage occur in valves or pistons. The leakage will be more with the increase in pressure , as in fig  .  .

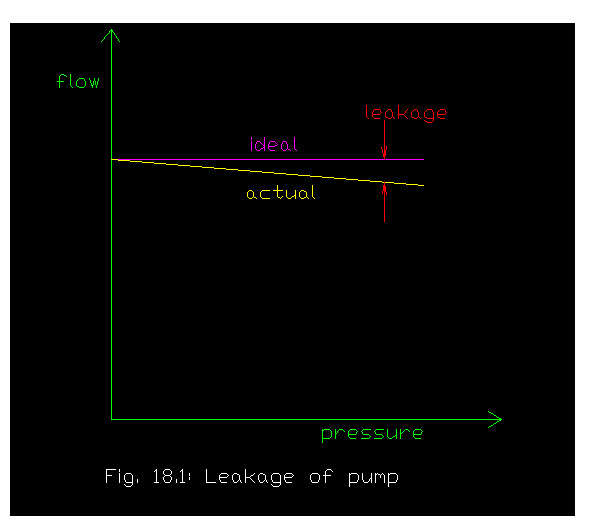
L 20 fig.20.1

20.3 Volumetric Efficiency

The volumetric efficiency may be defined as the ratio of actual flow rate to the theoretical flow rate

            Let

                        Qa       =          actual flow rate

                        Qt        =          theoretical flow rate

                        \[\eta \]vol    =     volumetric efficiency

 

                        \[\eta \]vol        =   \[\frac{{{\text{Qa}}}}{{{\text{Qt}}}}\]        x 100

The piston pump is the most suitable example of positive displacement pump but other pumps like gear pump, lobe pump, screw pump and vane pump also come under the same category and calculations can be made accordingly.

20.4 Power of the Pump Shaft

It can be defined as the mechanical power transmitted to the pump shaft by the shaft of power source. It is basically product of torque and speed of the shaft. Hence it can be given as –

 

                                     Ps       =          ω x t

                                     Ps       =          shaft power

                                     ω        =          angular speed

t          =          torque

The angular speed of the shaft isfined as the  in radians per second and torque transmitted is in Nm. Now if the torque is transmitted in Nm and speed in revolution per second (rpm) the the equation can be deduced as below-

L 20 eq.2

20.5 Fluid Power Calculations

It can be defined as the energy per second by the fluid in the form of pressure and the quantity of fluid. It is product of fluid quantity (flow rate)  and the differential pressure. Hence

                                                            Pf         =          Q x Dp

Where                                                  Pf            =          Fluid power

                                                            Q         =          flow rate , m3/s

                                                            Δp        =          differential pressure, N/m2

20.6 Overall Efficiency

It can be defined as the ratio of fluid power to the shft power or in other words ratio of output power to the input power. The input power is greater than the ouput power due to leakages in the sysem and friction between the moving parts. Hence overall efficiency can be given as-

L 20 eq.3

Example 1

A pump delivers 10x10-3 m3 /min with a pressure rise of  680 N/m2 .The shaft speed of 1400rpm and the nominal displacement is 8.2 cm3/rev. The applied torque is 12 Nm. Determine the followings-

a) Shaft power

b) Volumetric efficiency

c) Overall efficiency

Soln.

L 20 eq.4

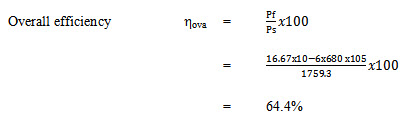
L 20 eq.5 

Example 2

The pump is operating at a speed of 410 rpm and the pressure difference over the hydraulic pump is 82 bar. The nominal displacement is 5.2 cm3/rev. The overall efficiency is 83% and the volumetric efficiency

Is 91%  calculate the followings-

a) Theoretical flow rate

b) Actual flow rate

c) Fluid power

d) Shaft power

e) Torque transmitted

Soln.

Given

                                     N        =          410 rpm

                                                =          410/60 rps

                                                =          6.83 rps

Theoretical flow rate    Qt        =         Nominal displacement x speed

                                                 =         5.2 x 6.83

                                                 =         35.51 cm3/s

                                                 =         35.51x10-6m3/s

Volumetric efficiency \[\eta \]vol  =   \[\frac{{{\text{Qa}}}}{{{\text{Qt}}}}\]        x 100

                                    Qa       =          Qt x\[\eta \]vol /100

                                               =          35.51x10-6x91/100

                                               =          32.3 x 10-6 m3/s

Now fluid power                     Pf        =          Qa x Δp

                                             Qa      =          32.3 x 10-6 m3/s

                                             Δp      =          82 N/m2

                                                                     =          82x105N/m2

                                            Pf        =          32.3x10-6x82 x105 watts

                                                       =          264.86 watts

Shaft power                           Ps       =    \[\frac{{2\pi N}}{{60}}\]   

Overall efficiency                    \[\eta \]ova       =      \[\frac{{{\text{Pf}}}}{{{\text{Ps}}}}x100\]  

 

                                             Ps       =          Pf x 100/hova

                                                                      =          264.86 x 100/83

                                                                      =          319.1 watts

                                              Ps      =         \[\frac{{2\pi x410x}}{{60}}\]

                                                 t         =          319.1x60/ \[2\pi x410\] Nm

                                                            =          7.43 Nm

Last modified: Tuesday, 18 March 2014, 4:02 AM