Machine Design 3(2+1)

LESSON 32 DESIGN OF CURVED BEAMS

Figure 32.1 Distribution of Stress in a Curved Beam

In stress analysis of curved beam, following assumptions are made:

Let                   R_o           = radius of outer fibre (mm)

R₁        = radius of inner fibre (mm)

R         = radius of centroidal axis (mm)

R_N        = radius of neutral axis (mm)

h_i         = distance of inner fibre from neutral axis (mm)

h_o            = distance of outer fibre from neutral axis (mm)

M         = bending moment with respect to centroidal axis (N-mm)

A         = area of the cross-section (mm2)

Eccentricity between centroidal and neutral axis is given by,

Bending stress in any fibre, at distance ‘y’ from the neutral axis, is given by,

Equation indicates that stress has hyperbolic distribution with respect to y. Maximum stress occurs either at the inner fibre or at the outer fibre.

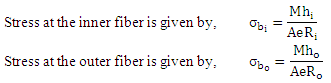
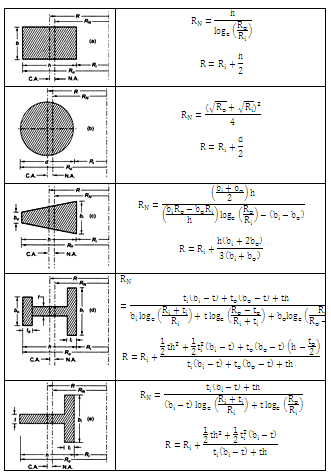
In symmetrical cross-sections (circular, rectangular etc.), maximum bending stress always occurs at the inner fibre. But for unsymmetrical sections, stress must be calculated for inner and outer fibre to find its maximum value. Value of e is generally very small but its precise calculation is very important to avoid error in stress determination. Expressions for calculation of R and R_N, for some standard cross-sections are given in table 32.1.

Table 32.1 R and R_N for some Standard Cross-sections

 

 

References

1. Design of Machine Elements by VB Bhandari

2. Analysis and Design of Machine Elements by V.K. Jadon

3. Design of Machine Elements by C.S. Sharma & K. Purohit

4. Machine Design by P.C. Sharma & D.K. Aggarwal

5. Machine Design by R.S. Khurmi