Engineering Physics 3(2+1)

LESSON 2. Classification of Magnetic Material

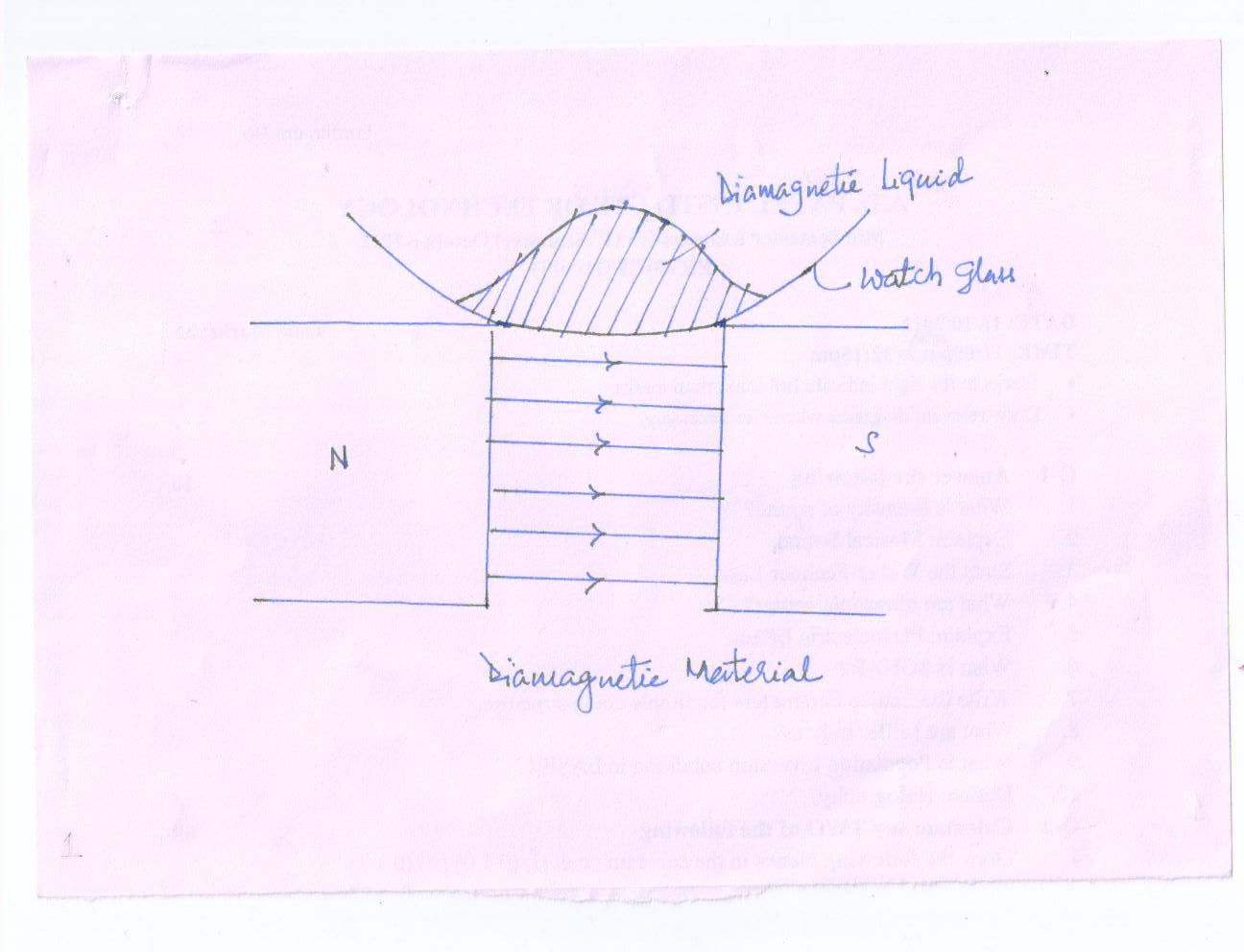When a bar of diamagnetic material is placed in an external magnetic field, the magnetic induction  becomes less than magnetizing field H

The permeability  \[{\mu _r}\] of diamagnetic material is less than one but positive.

The diamagnetic susceptibility values  X_D are small negatives. The susceptibility values are unaffected by changes in temperature.

Langevin’s theory of Diamagnetism

Suppose the electron is moving around the nucleus in an atom.

Let  m - mass, e - charge, r₁ - radius of the orbit, V  - liner velocity and  W_O- angular velocity respectively.

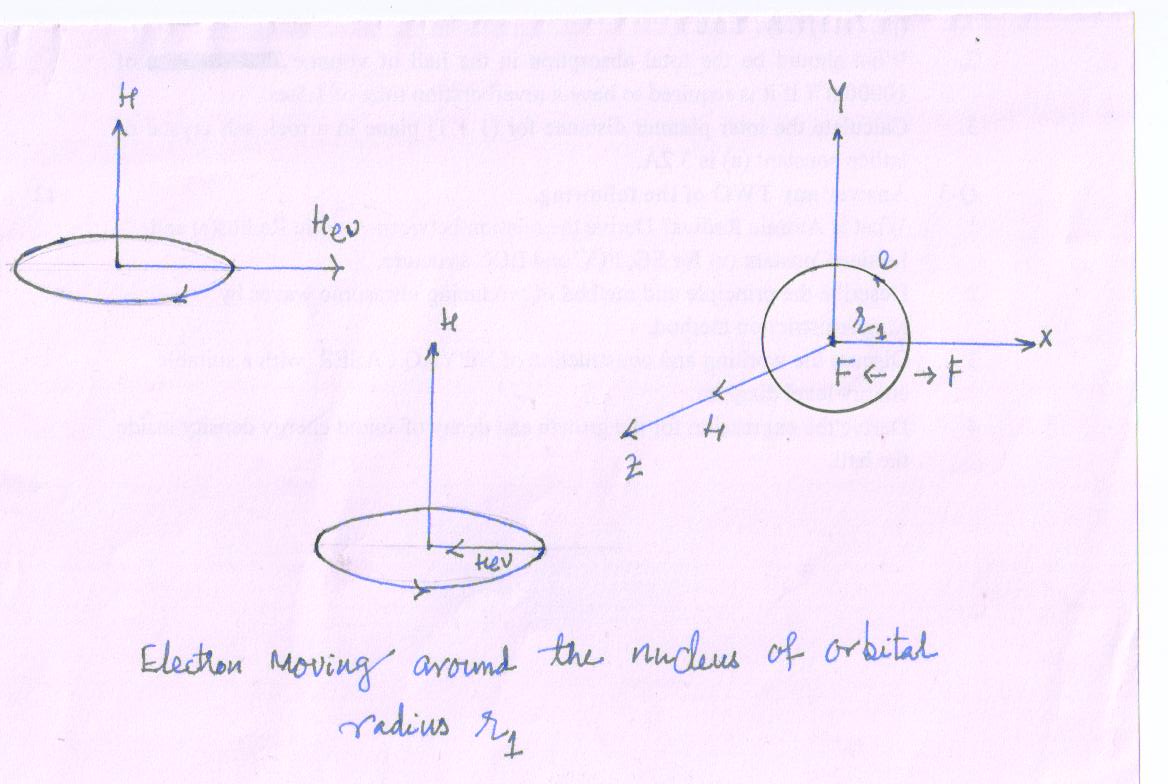
The revolving electron moves in a circular orbit due to the electrostatic force between the electron and the nucleus, which is balanced by centrifugal force.

 F =  \[{{m{v^2}} \over {{r_1}}}\] = \[m\omega _o^2{r_1}\] ; \[v={r_{1}}{\omega _o}\]; …….(1)

Let  H be the intensity of the applied magnetic field which acts perpendicular to the plane of the orbit, say, along z-axis.

Now force,

F = Hev……………(2) act on the electron due to the magnetic field.

The direction of the force is given by Fleming’s left hand rule.

When the electron is moving in clock wise direction, the force is directed outwards along the radius and when the electron is moving in anticlockwise direction, this force is directed inwards. The effect of applied field is only a precessorial motion of the orbit without any change in its form. It is called Larmor precession.

Due to this motion, the angular velocity of the electron is changed from say \[{\omega _o}\] to \[\omega\].

Then

 \[m{\omega ^2}{r_1}=F=m\omega _o^2{r_1} \pm F\]

( \[m{\omega ^2}-m\omega _o^2){r_1}\] = change of radial force = Hev

( \[{\omega ^2}-\omega _o^2)m{r_1}\] = Hev

\[\left({\omega-{\omega _o}}\right)\] = \[{{He{r_{1}}\omega }\over{m{r_1}\left({\omega+{\omega _o}}\right)\]   ……………..(3)

Let ω - ω _o = Δω and ω + ω _o =  2ω

Δω = \[{He\omega}\over{2m\omega c}\]………….. (4)

 C is velocity of light introduced to convert electrostatic unit of electronic charge into electromagnetic unit.

This change of angular velocity (frequency) is termed Larmor Frequency. This change in frequency of the electronic motion produces a net current

\[di=- e{{\omega}\over{2\pi }}\]………(5)

Using equn (4) in equn (5)

di=\[{{-{e^2}H}\over{4\pi mc}}\] ……………..(6)

Due to this additional current, the additional magnetic moment produced is

\[d\mu={{-{e^2}Hr_1^2\pi }\over{4m{c^2}}}\]…….(7)

The negative sign indicates that the direction of the induced moment is opposite to the direction of the applied field, which is the intrinsic property of diamagnetism. If there are z electronic orbits in an atom (z  -atomic number) the total induced magnetic moment in each atom is

See From Fig.1(5)

\[r_1^2={x^2} + {y^2}\]

\[r_1^2\]  is the mean square of the perpendicular distance of the electron from the field axis through the nucleus.  If   is the mean value of all possible orbital radii, then

 \[r_1^2\] = \[{x^2} + {y^2} + {z^2}\]………….(9)

For a spherically symmetrical charge distributions

\[{x^2} = {y^2} = {z^2}\]

So \[r_1^2 = 2{x^2}= {2{r^2}} \over 3}\]    ……(10)

Using equation (10) in equation (8) we get ,

For solid containing N atoms per unit volume, the total magnetic moment per unit volume or magnetization is

The diamagnetic susceptibility   is the ratio of induced magnetization to the magnetic field

This is classical Langevin’s expression for diamagnetic susceptibility.

The diamagnetic susceptibility is independent of the field strength and temperature, which was later proved to be correct by Curie’s experimental observation.  

Paramagnetism

It may be defined as a type of magnetism in which the material gets weakly magnetized in the same direction as that of the applied magnetic field.

The materials which exhibit paramagnetism are alkali metals, transition metals, and rare earth elements.

The origin of paramagnetism arises from   the presence of permanent magnetic moments in the atoms or molecules.

The permanent magnetic moments in a single atom are created due to

The moving of an electron is in a circular or elliptical orbit around the nucleus.

The motion of an electron is about its own axis (spin).

It has been observed that the magnetic moments created due to orbital motion of electrons disappear due to the effect of the electric field of the neighboring charges. But magnetic moments due to the spin motion of the electrons remain un affected by this field.

It will be interesting to add that the spin magnetic moments are composed of two groups.

One of the groups contains electrons with clockwise spin and the other with anticlockwise spin.

In the absence of an electric field, these magnetic moments are randomly distributed, or in other words they have no mutual interactions among them.

This is called paramagnetism.

In presence of magnetic field, the moments have a tendency to turn towards the direction of the field.

If no opposing forces act, a complete alignment of the atomic moments will be produced and the sample as a whole acquires a very large magnetization in the direction of the field.

However, thermal agitation of the atoms opposes this tendency and tends to randomize the atomic the atomic dipole moments.

The results are only a partial alignment in the field direction and hence paramagnetic materials exhibits weak inherent magnetization and a small positive susceptibility.

An increase in thermal energy will increase the randomizing effect on the alignment of magnetic dipoles along the field direction and hence decrease the susceptibility.   

Properties of Paramgnetism

• Para magnetic material when placed in a magntic field acquires a feeble magnetization in the same sense as the applied field. Platinum, Aluminum, Copper, Sulphate and Nickle.solutions are the example of paramgentism.

• These substances when exposed to a non-uniform magnetic field experience an attractive force toward the stronger part of the field. For example, if we place a paramagnetic liquid in a watch glass and place it over a non-uniform magnetic field, the liquid moves toward the poles as the field is strongest near the poles.

  

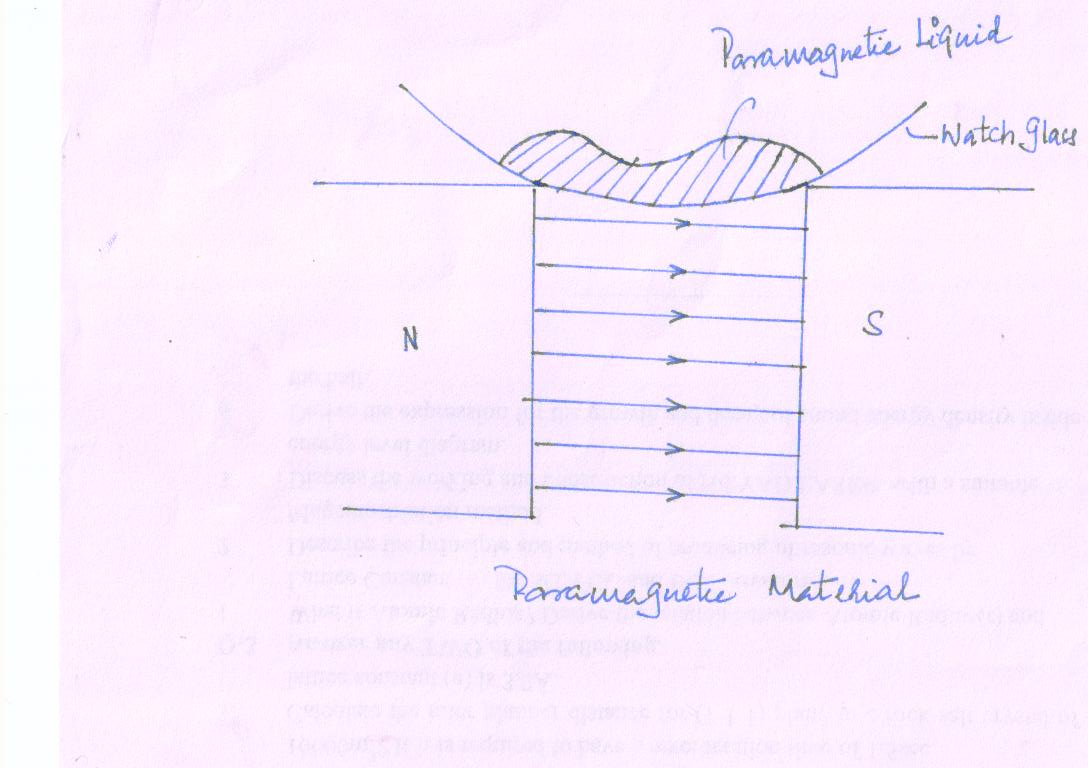
• When paramagnetic materials are placed in uniform magnetic field, the magnetic induction  becomes more than the magnetizing field  and thus the relative permeability is slightly greater than unity.

• The paramagnetic susceptibility is however small but positive.

• The susceptibility is inversely proportional to the operating temperature. Thus with increase in temperature the X value decreases and becomes negative at elevated high temperatures to exhibits diamagnetic properties.

Langevin’s theory of Paramgetism

In absence of external magnetic field, the dipoles are oriented along different directions, such that the resultant sum of all projections of magnetic moments on any reference line is zero.

When the external field is applied, the state of magnetization depends upon the following two factors:

The applied magnetic field- it align the magnetic axes of molecules along the field direction.

The thermal agitation- It is disorganizes the orderly state produced by the applied field.

For the equilibrium state, the following two kinetic theory principles are used

(1) The number of molecules having orientation, inclined at an angle \[\theta\] with the given line of reference is directly proportional to the \[\sin \theta d\theta\]

(2) As per of equpartition of energy, the number of molecules whose potential energy is proportional to ,energy is proportional to , 

w is magnetostatic energy, 

k is Boltzmann factor and 

T is absolute temperature.

Let us consider a molecular magnetic moment of  μ , inclined at an angle \[\theta\]  with respect to the external magnetic field of induction B

The intensity of magnetization may be derived as follow

We know that the resolved component of magnetic moment of each molecule along the field direction is μ cos \[\theta\] . Thus the resultant magnetic moment due to molecules is dN μ cos \[\theta\] . Hence the magnetic moment of all N  molecules in unit volume which is equal to I is given by

From graph

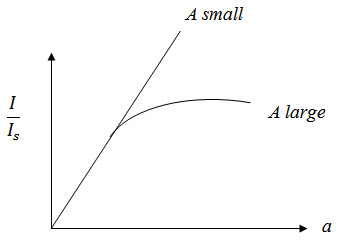
a is small and linear,thus