Engineering Physics 3(2+1)

LESSON 16. Bands in Solid

(i) In home, we use a variety of electronic systems: radios, TVs, VCRs, CD players, telephone answering machines, PCs, microwave ovens, pocket calculators, digital watches, etc.

(ii) Round-the-globe communication via microwave or fiber-optic links and satellites, and access to internets has been possible with advances in electronics. This has shaped the global village.

(iii) Sophisticated electronic instruments are used for researches in various fields of science and engineering.

(iv) The commercial and industrial sectors rely on electronic communication, information processing, and control systems.

(v) Electronic radar systems are employed for a safe flight from one airport to another. A modern aircraft is equipped with electronic sensors and computers.

(vi) Electronic communication and radars play a vital role in meteorology, defense, and military services.

(vii) Modern medical practice relies on precise diagnostics and monitoring electronic systems. For better times, and at times for worse, electronics has shaped our lives. Our living standards have improved, but we are also at the peril of deadly weapons that would not have appeared without the progress in electronics.

Energy Bands in Solids

The allowable discrete values of n show that all energies are not permitted for the electrons. The electrons can have only certain discrete energies corresponding to the different integral values of n. In other words, the electron energy is quantized. The allowable energies are represented by horizontal lines in a diagram, called the energy level diagram of the atom.

When an electron jumps from a higher energy level E₁ to a lower energy level E_h  , an electromagnetic radiation of frequency is emitted, where

\[v={\rm{}}{{{E_h}-{\rm{}}{E_l}}\over h}\] …………..(2)

 h is Being Planck’s constant.

On the contrary, on absorbing a photon of energy hν, an electron initially at the energy state E₁ can move to the energy state hν .

An electron normally occupies the lowest energy state, called the ground level, in the atom. The other higher lying energy levels are called the excited levels of the atom. By absorbing more and more energies, an electron can move into excited states which are farther and farther away from the nucleus. If the energy is sufficiently high, the electron can overcome the attraction of the nucleus and gets detached from the atom. The energy required for this to occur is known as the ionization potential. The energy level corresponding to  in n =  ∞ See Above Fig. represents the ionization level. As the electrons are electrostatically attracted by the positively charged nucleus, the allowed energies for the electrons are negative. The ionization level represents the zero level of energy. The energies become more and more negative with decreasing values of n .

The wavelengths emitted from the atom due to electronic transitions from higher energy states to lower ones give the spectral lines characterizing the atom. To explain the details of the spectral lines of some elements, improvements over the simple Bohr model have been made. Quantum mechanical treatments have introduced four quantum numbers, designated by n, l , m_l  and m_s . The quantum numbers can take the following values:

n, = 1, 2, 3...

l = 0, 1, 2,... (n – 1)

m_l = 0, ± 1, ± 2,...,± l

m_s = ±1/2

The quantum number n, called the principal quantum number, primarily determines the energy of the orbital electrons. The quantum number  l measures the angular momentum of the electron, and is referred to as the orbital angular momentum quantum number. The number ml gives the splitting of the energies for a given n and l in a magnetic field, and is called the magnetic quantum number. The quantity ms, known as the spin quantum number, shows that the spin of the electron about its own axis is quantized.

The state of an electron in the atom is uniquely specified by the four quantum numbers. This is a result of Pauli’s exclusion principle. The principle states that no two electrons in an electronic system can occupy the same quantum state described by the same set of four quantum numbers n , l  , m_l and m_s. Electronic Shells

The specific value of the principal quantum number n determines an electronic shell. All the electrons of a given atom having the same value of n belong to the same electronic shell. L diagram of the letters K, L, M, N, ... denote the shells for n = 1, 2, 3, 4, ... , respectively. The different values of l for a given n define the subshells for the shell. The subshells are represented by s, p, d, f, ... corresponding to  l = 0, 1, 2, 3, ... , respectively.

For  n= 1, there are two states corresponding to l = 0,  m_l= 0, and ms = ± 1/2. These two states are known as 1 states. For n = 2, we have two 2s  states corresponding to  l= 0, = 0, and  m_s ±  1/2 . In addition, there are six states for n = 2,  l= 1, m_l = –1, 0, + 1, and  m_s = ± 1/2.

These are 2p  states. The total number of electrons in the K shell ( n = 1) is thus 2, and that in the L shell (n = 2) is 2 + 6 = 8. Similarly, it can be shown that a maximum of 10 electrons can be accommodated in a d subshell, a maximum of 14 electrons in an f subshell, and so on. The number of protons in the nucleus is the atomic number Z. Since the atom is electrically neutral, the number of orbiting electrons is also Z. For sodium, Z = 11. The electronic configuration of the sodium atom is 1s² 2s² 2p² 3s¹,  where the superscripts denote the number of electrons in a particular subshell. Clearly, the sodium atom has one electron in the outermost subshell.

Energy Bands in Crystals

A crystal is a solid consisting of a regular and repetitive arrangement of atoms or molecules (strictly speaking, ions) in space. If the positions of the atoms in the crystal are represented by points, called lattice points, we get a crystal lattice. The distance between the atoms in a crystal is fixed and is termed the lattice constant of the crystal.

To discuss the behavior of electrons in crystal, we consider an isolated atom of the crystal. If  Z is the atomic number, the atomic nucleus has a positive charge Ze. At a distance r from the nucleus, the electrostatic potential due to the nuclear charge is (in SI units)

\[{V_{r={\rm{}}{{Ze}\over {4\pi {\varepsilon _o}r}}}}\] …………..(3)             

Where   is the permittivity of free space. Since an electron carries a negative charge, the potential energy of an electron at a distance  from the nucleus is

\[{E_p}\left(r\right)=eV\left(r\right)={{Z{e^2}}\over{4\pi{\varepsilon_o}r}}\].……….(4)

 is positive while  is negative. Both  and   are zero at an infinite distance from the nucleus.

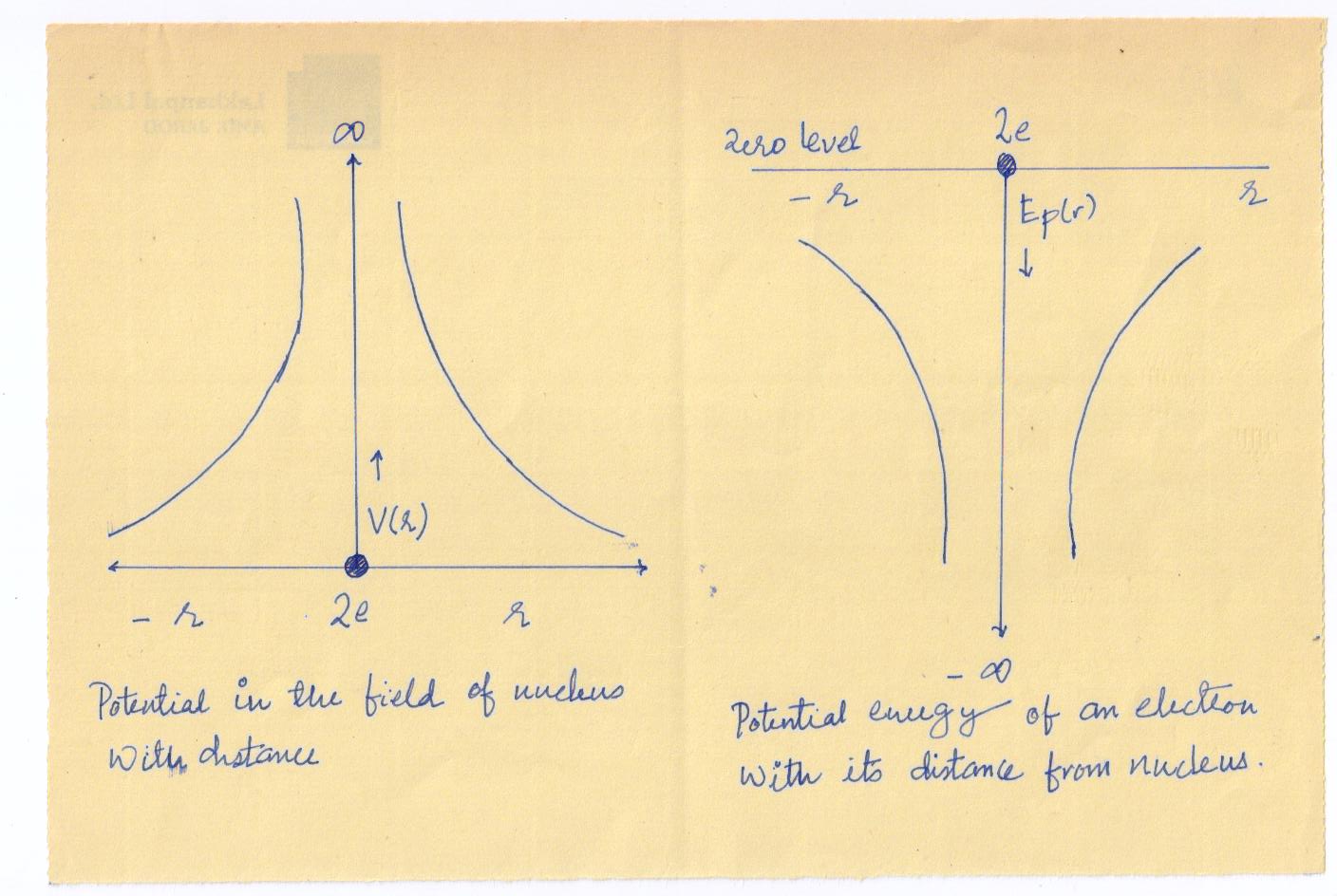
Fig  show the variation of  V_r   and E_p(r) , respectively with r .

We now consider two identical atoms placed close together. The net potential energy of an electron is obtained as the sum of the potential energies due to the two individual nuclei. In the region between the two nuclei, the net potential energy is clearly smaller than the potential energy for an isolated nucleus.

The potential energy along a line through a row of equispaced atomic nuclei, as

in a crystal, is diagrammatically shown in

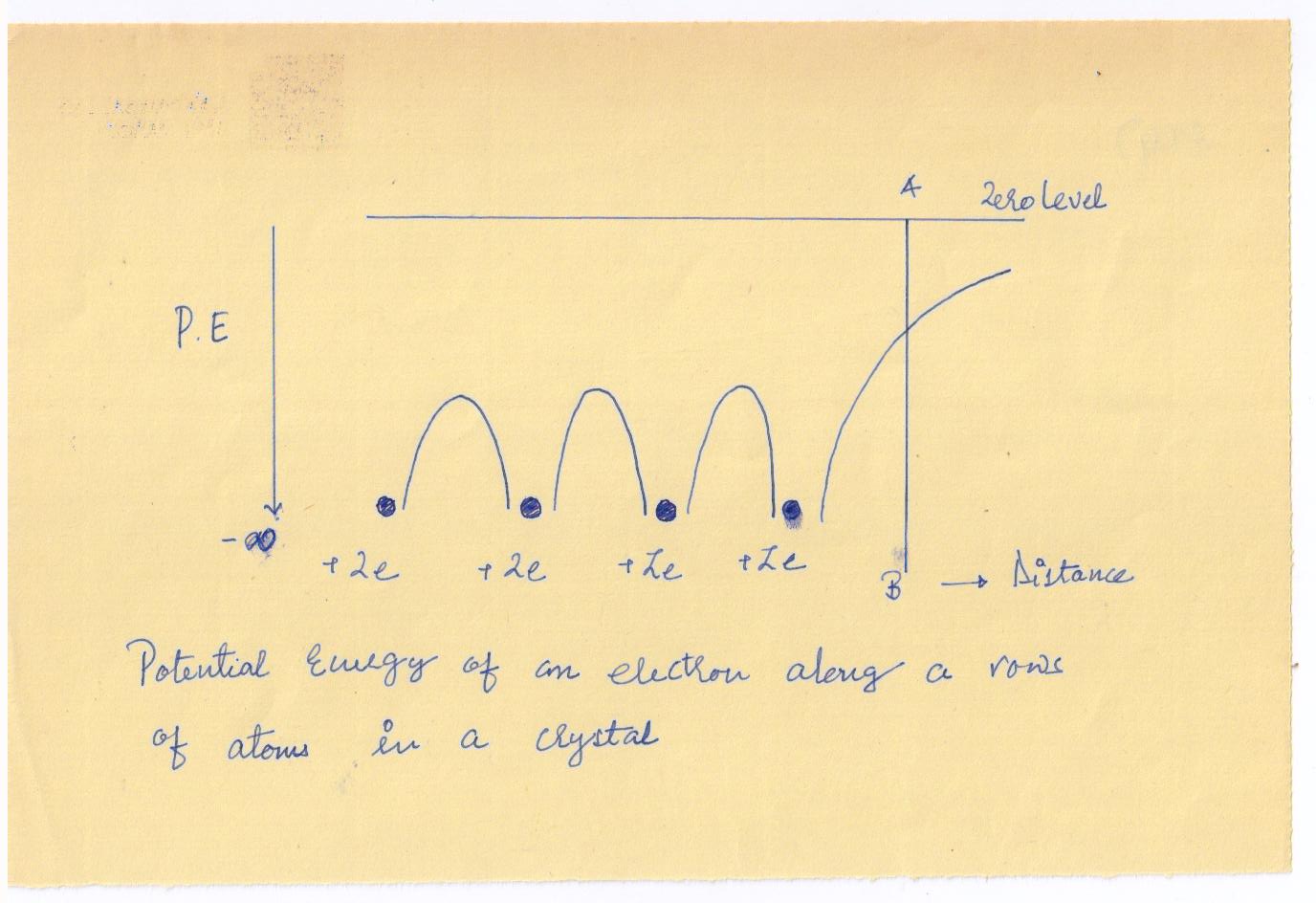
The potential energy between the nuclei is found to consist of a series of humps. At the boundary AB of the solid, the potential energy increases and approaches zero at infinity, there being no atoms on the other side of the boundary to bring the curve down.

The total energy of an electron in an atom, kinetic plus potential, is negative and have discrete values. These discrete energy levels in an isolated atom are shown by horizontal lines in

When a number of atoms are brought close together to form a crystal, each atom will exert an electric force on its neighbors. As a result of this interatomic coupling, the crystal forms a single electronic system obeying Pauli’s exclusion principle. Therefore, each energy level of the isolated atom splits into as many energy levels as there are atoms in the crystal, so that Pauli’s exclusion principle is satisfied. The separation between the split-off energy levels is very small. This large number of discrete and closely spaced energy levels forms an energy band. Energy bands are represented schematically by shaded regions in See Above Fig.The width of an energy band is determined by the parent energy level of the isolated atom and the atomic spacing in the crystal. The lower energy levels are not greatly affected by the interaction among the neighboring atoms, and hence form narrow bands. The higher energy levels are greatly affected by the interatomic interactions and produce wide bands. The interatomic spacing, although fixed for a given crystal, is different for different crystals. The width of an energy band thus depends on the type of the crystal, and is larger for a crystal with a small interatomic spacing.  The width of a band is independent of the number of atoms in the crystal, but the number of energy levels in a band is equal to the number of atoms in the solid. Consequently, as the number of atoms in the crystal increases, the separation between the energy levels in a band decreases. As the crystal contains a large number of atoms (), the spacing between the discrete levels in a band is so small that the band can be treated as continuous.

The lower energy bands are normally completely filled by the electrons since the electrons always tend to occupy the lowest available energy states. The higher energy bands may be completely empty or may be partly filled by the electrons. Pauli’s exclusion principle restricts the number of electrons that a band can accommodate. A partly filled band appears when a partly filled energy level produces an energy band or when a totally filled band and a totally empty band overlap.

As the allowed energy levels of a single atom expand into energy bands in a crystal, the electrons in a crystal cannot have energies in the region between two successive bands. In other words, the energy bands are separated by gaps of forbidden energy.

The average energy of the electrons in the highest occupied band is usually much less than the zero level marked in See See Above Fig.. The rise of the potential energy near the surface of the crystal, as shown in See Above Fig. serves as a barrier preventing the electrons from escaping from the crystal. If sufficient energy is imparted to the electrons by external means, they can overcome the surface potential energy barrier, and come out of the crystal surface.