IE: LESSON 8. Orifices

LESSON 8. Orifices

8.1 Free Flow Orifice

Orifices may be used to measure rates of flow when the size and shape of the orifice and head acting upon them are known. Orifices used in measurement of irrigation water are commonly circular or rectangular in shape and are generally placed in vertical surfaces, perpendicular to the direction of channel flow. The section where contraction of the jet is maximal is known as the vena contracta. The vena contracta of a circular orifice is about half the diameter of the orifice itself.

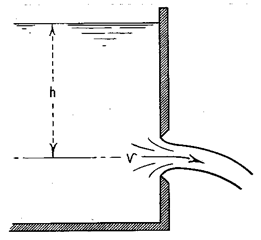
Fig.8.1. Free discharging through orifice.

(Source:http://www.usbr.gov/pmts/hydraulics_lab/pubs/wmm/chap02_08.html, accessed on Aug 21, 2013)

Derivation of Equation

Velocity of flow through orifice

V= ............(8.1)

Where, h=head

Discharge through orifice. Q=AV

...........(8.2)

Where, C_d= discharge coefficient

Co-efficient of Velocity (C_v): It is defined as the ratio of the actual velocity of a jet of liquid at vena-contracta and the theoretical velocity of the jet. It is mathematically expressed as:

.......(8.3)

.......(8.4)

Where, V= actual velocity and h = head.

Co-efficient of Contraction (C_c): It is defined as the ratio of the area of the jet at vena-contaracta to the orifice. It is mathematically expressed as:

........(8.5)

Co-efficient of Discharge (C_d): It is defined as the ratio of the actual discharge from an orifice to the theoretical discharge from the orifice. It is mathematically expressed as:

.......(8.6)

Cd = Cv * Cc .........(8.7)

8.2 Submerged Orifice

8.2.1 Fully Submerged Orifice

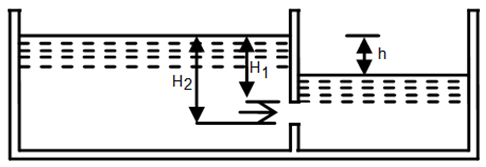
Fig.8.2. Fully submerged orifice.

(Source:http://www.codecogs.com/library/engineering/fluid_mechanics/orifice/geometry/index.php accessed on August 21, 2013)

In fully sub-merged orifice, the outlet side is fully sub-merged under the liquid and it discharges a jet of liquid into the liquid of the same kind. It is also called totally drowned orifice. Discharge through fully sub-merged orifice is calculated as

......(8.8)

Where,

H₁= height of water above the top of the orifice on the upstream side

H₂= height of water above the bottom of the orifice

H= difference in water level

b= width of orifice

8.3.2 Partially Submerged Orifice

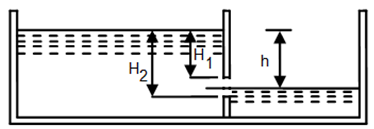
Fig. 8.3. Partially submerged orifice.

(Source:http://www.codecogs.com/library/engineering/fluid_mechanics/orifice/geometry/index.php accessed on August 21, 2013)

In this case, its outlet side is partially sub-merged under liquid. The discharge through partially sub-merged orifice is calculated as:

.......(8.9)

The first term in RHS in Eq. (8.9) represents flow through drowned (submerged portion of orifice same as Eq. (8.8)), whereas the second term represents discharge through free portion.

Example 8.1:

The head of water over an orifice of diameter 100 mm is 10 m. The water coming out from orifice is collected in a circular tank of diameter 1.5 m. The rise of water level in the tank is 1.0 m in 25 seconds. Also the co-ordinates of a point on the jet, measured from vena-contracta are 4.3 m horizontal and 0.5 m vertical. Find the coefficients, C_d, C_v and C_c.

Solution:

Given,

Head H= 10 m.

Diameter of orifice d= 100 mm = 0.1 m

So, area of orifice a= π/4 X (0.1)² = 0.007853 m²

Diameter of measuring tank, D= 1.5 m

So, area = π/4 X (1.5)² = 1.767 m²

Rise of water, h= 1 m

Time t = 25 sec

Horizontal distance x= 4.3 m

Vertical distance y= 0.5 m

Now, theoretical velocity,

V_th=

=14m/s.

Theoretical discharge,

Q_th = V_th X area of the orifice

= 14 X 0.077854 = 0.1099m³/s

Actual discharge,

=0.07068 m³/s

So,

C_d=

We know,

C_v=

And

C_c= 0.669

Example 8.2:

Find the discharge through a fully sub-merged orifice of width 2 m if the difference of the water levels on the both sides of the orifice is 50 m. The height of water from top and bottom of the orifice are 2.5 m and 2.75 m respectively. Take C_d= 0.6.

Solution:

Given,

Width of the orifice b = 2 m

Difference in water level H= 50 cm = 0.5 m

Height of water from top of orifice H1= 2.5 m

Height of water from bottom of orifice H1= 2.75 m

Now, discharge through fully submerged orifice is