Soil & Water Conservation Engg. 3(2+1)

Lesson 16 Soil Loss/Sediment Yield Estimation

16.1 Estimation of Soil Loss

The control of erosion is essential to maintain the productivity of soil and to improve or maintain downstream water quality. The reduction of soil erosion to tolerable limits necessitates the adoption of properly planned cropping practices and soil conservation measures. Several methods exist for the measurement of soil loss from different land units. These include the measurements from runoff plots of various sizes for each single land type and land use, small unit source watersheds, and large watersheds of mixed land use. However, to estimate soil erosion, empirical and process based models (equations) are used. Universal Soil Loss Equation (USLE) is an empirical equation. It estimates the average annual mass of soil loss per unit area as a function of most of the major factors affecting sheet and rill erosions. Estimating soil loss is considerably more difficult than estimating runoff as there are many variables, both natural such as soil and rainfall and man-made such as adopted  management practices. The soil loss considerably depends on the type of erosion. As a result, models, whether empirical or process-based, are necessarily complex if they are to include the effect of all the variables.

For some purposes, meaningful and useful estimates of sediment yield can be obtained from models, and the best example is the estimation of long-term average annual soil loss from a catchment by using the Universal Soil Loss Equation (USLE).

16.2 The Universal Soil Loss Equation (USLE)

The filed soil loss estimation equations development began in 1940 in USA. Zing (1940) proposed a relationship of soil loss to slope length raised to a power. Later in 1947, a committee chaired by Musgrave proposed a soil-loss equation having some similarity to the present day USLE. Based on nearly 10,000 plot year runoff plot data, Wischmeier and Smith (1965) developed the universal soil loss equation, which was later refined with more recent data from runoff plots, rainfall simulators and field experiences. It is the most widely used tool for estimation of soil loss from agricultural watersheds for planning erosion control practices. The USLE is an erosion prediction model for estimating long term averages of soil erosion from sheet and rill erosions from a specified land under specified conditions (Wischmeier and Smith, 1978).

It provides an estimate of the long-term average annual soil loss from segments of arable land under various cropping conditions. The application of this estimate is to enable farmers and soil conservation advisers to select combinations of land use, cropping practice, and soil conservation practices, which will keep the soil loss down to an acceptable level. The equation (USLE) is presented as below.

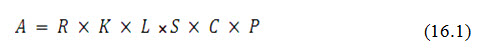
where, A = soil loss per unit area in unit time, t ha^-1 yr ^-1, R = rainfall erosivity factor which is the number of rainfall erosion index units for a particular location,  K = soil erodibility factor - a number which reflects the susceptibility of a soil type to erosion, i.e., it is the reciprocal of soil resistance to erosion, L = slope length factor, a ratio which compares the soil loss with that from a field of specified length of 22.6 meters, S = slope steepness factor, a ratio which compares the soil loss with that from a field of specified slope of 9%, C = cover management factor - a ratio which compares the soil loss with that from a field under a standard treatment of cultivated bare fallow, and P = support practice factor - a ratio of  soil loss with support practice like contouring, strip cropping or terracing to that with straight row farming up and down the slope.

The factors L, S, C and P are each dimensionless ratios which allow comparison of the site for which soil loss is being estimated with the standard conditions of the database. Knowing the values of rainfall erosivity, soil erodibility and slope one can calculate the effectiveness of various erosion control measures with the purpose of introducing a cultivation system in an area with soil loss limited to the acceptable value.

Various factors associated with the above equation are discussed below.

• Rainfall Erosivity Factor (R)

It refers to the rainfall erosion index, which expresses the ability of rainfall to erode the soil particles from an unprotected field. It is a numerical value. From the long field experiments it has been obtained that the extent of soil loss from a barren field is directly proportional to the product of two rainfall characteristics: kinetic energy of the storm and its 30-minute maximum intensity. The product of these two characteristics is termed as EI or EI₃₀ or rainfall erosivity. The erosivity factor, R is the number of rainfall erosion index units (EI₃₀) in a given period at the study location. The rainfall erosion index unit (EI₃₀) of a storm is estimated as:

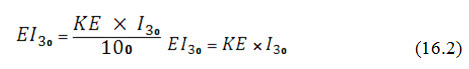
where,  KE = kinetic energy of storm in metric tones /ha-cm, expressed as

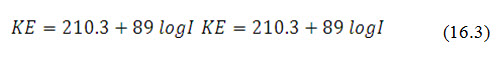
where,  I = rainfall intensity in cm/h, and Ι ₃₀ Ι₃₀ = maximum 30 minutes rainfall intensity of the storm.

The study period can be a week, month, season or year and this I₃₀ values are different for different areas. The storm EI₃₀ values for that length of period is summed up. Annual EI₃₀ values are usually computed from the data available at various meteorological stations and lines connecting the equal EI₃₀ values (known as Iso-erodent lines) are drawn for the region covered by the data stations for ready use in USLE.

• Soil Erodibility Factor (K)

The soil erodibility factor (K) in the USLE relates to the rate at which different soils erode. Under the conditions of equal slope, rainfall, vegetative cover and soil management practices, some soils may erode more easily than others due to inherent soil characteristics. The direct measurement of K on unit runoff plots reflect the combined effects of all variables that significantly influence the ease with which a soil is eroded or the particular slope other than 9% slope. Some of the soil properties which affect the soil loss to a large extent are the soil permeability, infiltration rate, soil texture, size and stability of soil structure, organic content and soil depth. These are usually determined at special experimental runoff plots or by the use of empirical erodibility equations which relate several soil properties to the factor K. The soil erodibility factor (K) is expressed as tons of soil loss per hectare per unit rainfall erosivity index, from a field of 9% slope and 22 m (in some cases 22.13 m) field length. The soil erodibility factor (K) is determined by considering the soil loss from continuous cultivated fallow land without the influence of crop cover or management.

The formula used for estimating K is as follows:

 

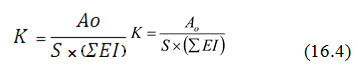
where, K = soil erodibility factor, A₀ = observed soil loss, S = slope factor, and ΣEI = total rainfall erosivity index.

Based on runoff plot studies, the values of erodibility factor K have been determined for use in USLE for different soils of India as reported by Singh et al. (1981). Values of K for several stations are given in Table 16.1.

Table 16.1. Values of K for Several Stations (Source: K. Subramanya, 2008)

Station	Soil Type	Computed Values of  K
Agra	Loamy sand, alluvial	0.07
Dehradun	Dhulkot silt, loam	0.15
Hyderabad	Red chalka sandy loam	0.08
Kharagpur	Soils from laterite rock	0.04
Kota	Kota clay loam	0.11
Ootakamund	Laterite	0.04
Rehmankhera	Loam, alluvial	0.17
Vasad	Sandy loam, alluvial	0.06

Topographic Factor (LS)

Slope length factor (L) is the ratio of soil loss from the field slope length under consideration to that from the 22.13 m length plots under identical conditions. The slope length has a direct relation with the soil loss, i.e., it is approximately equal to the square root of the slope length (L^0.5), for the soils on which runoff rate is not affected by the length of slope (Zing, 1940).

Steepness of land slope factor (S) is the ratio of soil loss from the field slope gradient to that from the 9% slope under otherwise identical conditions. The increase in steepness of slope results in the increase in soil erosion as the velocity of runoff increases with the increase in field slope allowing more soil to be detached and transported along with surface flow.

The two factors L and S are usually combined into one factor LS called topographic factor. This factor is defined as the ratio of soil loss from a field having specific steepness and length of slope (i.e., 9% slope and 22.13 m length) to the soil loss from a continuous fallow land. The value of LS can be calculated by using the formula given by Wischmeier and Smith (1962):

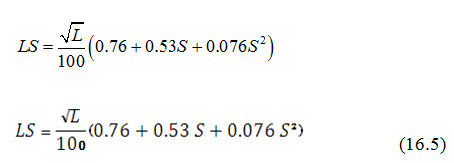
where, L = field slope length in feet and S = percent land slope.

Wischmeier and Smith (1978) again derived the following equation for LS factor in M.K.S. system, based on the observations from cropped land on slopes ranging from 3 to 18% and length from 10 to 100 m. The derived updated equation is:

 

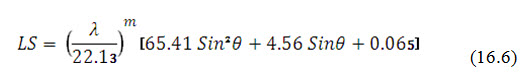
 where, λ = field slope length in meters, m = exponent varying from 0.2 to 0.5,  and θ = angle of slope.

Crop Management Factor (C)

The crop management factor C may be defined as the expected ratio of soil loss from a cropped land under specific crop to the soil loss from a continuous fallow land, provided that the soil type, slope and rainfall conditions are identical. The soil erosion is affected in many ways according to the crops and cropping practices, such as the kind of crop, quality of cover, root growth, water use by plants etc.  The variation in rainfall distribution within the year also affects the crop management factor, which affects the soil loss. Considering all these factors, the erosion control effectiveness of each crop and cropping practice is evaluated on the basis of five recommended crop stages introduced by Wischmeier (1960). The five stages are:

Period F (Rough Fallow): It includes the summer ploughing or seed bed preparation.

Period 1 (Seed Bed): It refers to the period from seeding to 1 one month thereafter.

Period 2 (Establishment): The duration ranges from 1 to 2 months after seeding.

Period 3 (Growing Period): It ranges from period 2 to the period of crop harvesting.

Period 4 (Residue or Stubble): The period ranges from the harvesting of crop to the summer ploughing or new seed bed preparation.

For determining the crop management factor the soil loss data for the above stages is collected from the runoff plot and C is computed as the ratio of soil loss from cropped plot to the corresponding soil loss from a continuous fallow land for each of the above five crop stages separately, for a particular crop, considering various combinations of crop sequence and their productivity levels. Finally, weighted C is computed. This factor reflects the combined effect of various crop management practices. Values of factor C for some selected stations of India are given in Table 16.2.

Table 16.2. Values of Crop Management Factors for Different Stations in India (Source: K Subramanya, 2008)

Station	Crop	Soil Loss, t ha -1y -1	Value of C
Agra	Cultivated fallow	3.80	1.0
	Bajra	2.34	0.61
	Dichanhium annualtu	0.53	0.13
Dehradun	Cultivated fallow	33.42	1.0
	Cymbopogon grass	4.51	0.13
	Strawberry	8.89	0.27
Hyderabad	Cultivated fallow	5.00	1.0
	Bajra	2.00	0.40

Support Practice Factor (P)

This factor is the ratio of soil loss with a support practice to that with straight row farming up and down the slope. The conservation practice consists of mainly contouring, terracing and strip cropping. The soil loss varies due to different practices followed. Factor P for different support practices for some locations of India is presented in Table 16.3.

Table 16.3. Different Values of Support Practice Factor (P) for Some Indian Locations (Source: K. Subramanya, 2008)

Station	Practice	Factor P
Dehradun	Contour cultivation of maize	0.74
	Up and down cultivation	1.00
	Contour farming	0.68
	Terracing and bunding in agricultural watershed	0.03
Kanpur	Up and down cultivation of Jowar	1.00
	Contour cultivation of Jowar	0.39
Ootacamund	Potato up and down	1.00
	Potato on contour	0.51

16.3 Use of USLE

There are three important applications of the universal soil loss equation.  They are as follows:

• It predicts the soil loss;

• It helps in identification and selection of agricultural practices; and

• It provides the recommendations on crop management practices to be used.

USLE is an erosion prediction model and its successful application depends on the ability to predict its various factors with reasonable degree of accuracy. It is based on considerably large experimental data base relating to various factors of USLE.

Based on 21 observation points and 64 estimated erosion values of soil loss obtained by the use of USLE at locations spread over different regions of the country, soil erosion rates have been classified into 6 categories. Areas falling under different classes of erosion are shown in Table 16.4.

Table 16.4. Distribution of various erosion classes in India (Source: K Subramanya, 2008)

Range (Tones/ha/year)	Erosion Class	Area (km2)
0-5	Slight	801,350
5-10	Moderate	1,405,640
10-20	High	805,030
20-40	Very high	160,050
40-80	Severe	83,300
>80	Very severe	31,895

16.4 Limitations of Universal Soil Loss Equation

The equation involves the procedure for assigning the values of different associated factors on the basis of practical concept. Therefore, there is possibility to introduce some errors in selection of the appropriate values, particularly those based on crop concept. Normally R and K factors are constants for most of the sites/regions in the catchment, whereas, C and LS vary substantially with the erosion controlled measures, used.  The following are some of the limitations of the USLE:

• Empirical

The USLE is totally empirical equation. Mathematically, it does not illustrate the actual soil erosion process. The possibility to introduce predictive errors in the calculation is overcome by using empirical coefficients.

• Prediction of Average Annual Soil Loss

This equation was developed mainly on the basis of average annual soil loss data; hence its applicability is limited for estimation of only average annual soil loss of the given area. This equation computes less value than the measured, especially when the rainfall occurs at high intensity. The storage basin whose sediment area is designed on the basis of sediment yield using USLE should be inspected after occurrence of each heavy storm to ensure that the sedimentation volume in the storage basin is within the limit.

• Non-computation of Gully Erosion

This equation is employed for assessing the sheet and rill erosions only but can not be used for the prediction of gully erosion. The gully erosion caused by concentrated water flow is not accounted by the equation and yet it can cause greater amount of soil erosion.

• Non-computation of Sediment Deposition

The equation estimates only soil loss, but not the soil deposition. The deposition of sediment at the bottom of the channel is less than the total soil loss taking place from the entire watershed. Nevertheless, the USLE can be used for computing the sediment storage volume required for sediment retention structures., Also the USLE equation can be used as a conservative measure of potential sediment storage needs, particularly where sediment basins ranges typically from 2-40 ha and runoff has not traveled farther distance and basin is intended to serve as the settling area. Again, if the drainage on any site is improperly controlled and gully erosion is in extensive form, then this equation underestimates the sediment storage requirement of the retention structure.

During the estimation of contribution of hill slope erosion for basin sediment yield, care should be taken as it does not incorporate sediment delivery ratio. This equation cannot be applied for predicting the soil loss from an individual storm, because the equation was derived to estimate the long term mean annual soil loss. The use of this equation should be avoided for the locations, where the values of different factors associated with the equation, are not yet determined.

16.5 Revised Universal Soil Loss Equation (RUSLE)

Over the last few decades, a co-operative effort between scientists and users to update the USLE has resulted in the development of RUSLE. The modifications incorporated in USLE to result the RUSLE are mentioned as under (Kenneth et.al. 1991):

• Computerizing the algorithms to assists the calculations.

• New rainfall-runoff erosivity term (R) in the Western US, based on more than 1200 gauge locations.

• Some revisions and additions for the Eastern US, including corrections for high R-factor areas with flat slopes to adjust splash erosion associated with raindrops falling on ponded water.

• Development of a seasonally variable soil erodibility term (K).

• A new approach for calculating the cover management term (C) with the sub-factors representing considerations of prior land use, crop canopy, surface cover and surface roughness

• New slope length and steepness (LS) algorithms reflecting rill to inter-rill erosion ratio

• The capacity to calculate LS products for the slopes of varying shapes

• New conservation practices value (P) for range lands, strip crop rotations, contour factor values and subsurface drainage.

16.6 Modified Universal Soil Loss Equation (MUSLE)

The USLE was modified by Williams in 1975 to MUSLE by replacing the rainfall energy factor (R) with another factor called as ‘runoff factor’. The MUSLE is expressed as

where, Y = sediment yield from an individual storm (in metric tones), Q = storm runoff volume in m³ and q_p = the peak rate of runoff in m³/s.

All other factors K, (LS), C and P have the same meaning as in USLE (equation 16.1). The values of Q and q_p can be obtained by appropriate runoff models. In this model Q is considered to represent detachment process and q_p is the sediment transport. It is a sediment yield model and does not need separate estimation of sediment delivery ratio and is applicable to individual storms. Also it increases sediment yield prediction accuracy. From modeling point of view, it has the advantage that daily, monthly and annual sediment yields of a watershed can be modeled by combining appropriate hydrological models with MUSLE.

Keywords: USLE, Rainfall Erosivity Factor, Soil Erodibility Factor, Soil Loss, Iso-erodent Lines, Topographic Factor.

References

Murty, V.V.N., Jha, M.K., 2009, Land and Water Management Engineering, Fifth Edition, Kalyani Publishers, pp.556-563.

Schwab et al., 1981, Soil and Water Conservation Engineering, Fourth Edition, Republic of Singapore: John Wiley & Sons, Inc., pp.97-104.

Subramanya, K., 2008, Engineering Hydrology, Third Edition, New Delhi: Tata McGraw-Hill, pp.374-379.

Suresh R., 2007, Soil and water conservation engineering, Second Edition, Standard Publishers Distributors, New Delhi, pp. 641-674.

Wischmeier, W.H., and Smith, D.D., 1978, Predicting Rainfall Erosion Losses - A Guide to Conservation Planning, U.S. Department of Agriculture, Agriculture Handbook No. 537.

Wischmeier, W.H., and Smith, D.D., 1965, Predicting Rainfall Erosion Losses from Crop Land East of the Rocky Mountains Guide for Selection of Practices Soil and Water Conservation, U.S. Department of Agriculture, Agricultural Handbook No. 282.

Zingg, R.W., 1940, Degree and length of land slope as it effects soil loss in runoff, Agric. Engng. 21: 59-64.

Suggested Readings

McCool DK, Brown LC, Foster GR, Mutchler CK, Mayer LD, 1987, Revised slope steepness factor for the Universal Soil Loss Equation, Trans ASAE 30: 1387–1396.

Narayana, V. V. Dhruva, 2002, Soil and water conservation research in India, ICAR, New Delhi, pp. 30-56.

Renard, K. G., G. R. Foster, G. A. Weesies and J. P. Portar, 1991, RUSLE, Revised universal soil loss equation, Journal of Soil and Water Conservation, 46:  30-33.

Singh, G., Ram Babu, and Subhash Chandra, 1981, Soil loss prediction research in India, Central Soil and Water Conservation Research & Training Institute, Dehradun, Bull. No. T-12/D-9, pp. 70.

Smith, D.D., and W.H. Wischmeier, 1962, Rainfall Erosion, (In) Advances in  Agronomy, 14: 109-148.

Williams, J.R., 1975, Sediment-yield prediction with Universal Equation using runoff energy factor, In: Present and Prospective Technology for Predicting Sediment Yield and Sources, U.S. Dept. Agric, ARS-S-40, pp. 244-252.

Renard, K. G., G. R. Foster, G. A. Weesies, D. K. McCool, and D. C. Yoder (Coordinators), 1995, Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE), U.S. Department of Agriculture, Agriculture Handbook No. 703 (In Review).

Foster, G. R., D. K. McCool, K. G. Renard and W. C. Moldenhauer, 1981, Conversion of the Universal Soil Loss Equation to SI metric units. Journal of Soil and Water Conservation 36(6): 355-359.