Watershed Hydrology 3(2+1)

Lesson 25 Derivation of Unit Hydrographs

 The area under each DRH is evaluated and the volume of the direct runoff obtained is divided by the catchment area to obtain the depth of ER. The ordinates of the various DRHs are divided by the respective ER values to obtain the ordinates of the Unit hydrograph.

 

Flood hydrograph used in the analysis should be selected to meet the following desirable features with respect to the storm responsible for them.

 

• The storms should be isolated storms occurring individually.

• The rainfall should be fairly uniform during the duration and should cover the entire catchment area.

• The duration of the rainfall should be 1/5 to 1/3of the basin lag.

• The rainfall excess of the selected storm should be high. A range of ER values of 1.0 to 4.0 cm is sometimes preferred. 

 

Example 1

A flood hydrograph of a river draining a catchment of 189 km² due to a 6 h isolated storm is in the form of a triangle with a base of 66 h and a peak ordinate of 30 m³/s occurring at 10 hours from the start. Assuming zero base flow, develop the 6-hour unit hydrograph for this catchment.

 

Answer

Given: catchment area (A) = 189 km²

Time interval = 6 h

Time base = 66 h

Peak = 30 m³/s

To find: 6-h UH for catchment

 

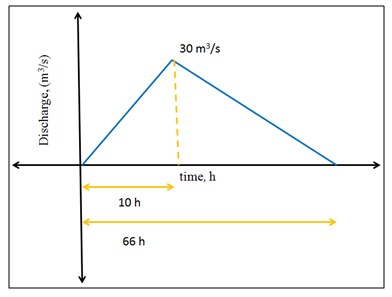
From figure

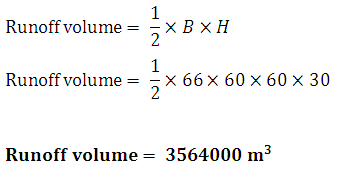
Therefore,

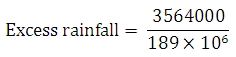
 Excess Rainfall =  1.89 cm

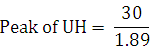
Peak of UH = 15.909 m²/s at 10 h from start 

25.2 Derivation of Unit Hydrograph from a Complex Storm

When suitable simple isolated storm are not available, data from complex storms of long duration will have to be used in unit-hydrograph derivation. 

Consider a rainfall excess made up of three consecutive durations of D-h and ER values of R₁, R₂, R₃.Figure 25.1 shows the ERR By base flow separation of the resulting composite flood hydrograph a composite DRH is obtained (Fig. 25.1).

 

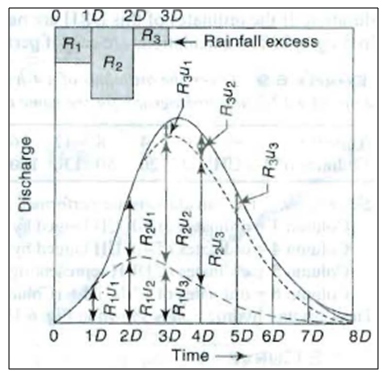
Fig. 25.1.Unit hydrograph from a Complex storm. (Source: Subramanya, 2008)

Let the ordinates of composite DRH be drawn at a time interval of D-h. At various time intervals 1D, 2D, 3D,… from the start of ERH, let the ordinates of the unit hydrograph be u₁, u₂, u₃,… and the ordinates of the composite DRH be Q₁, Q₂, Q₃,…,

Then

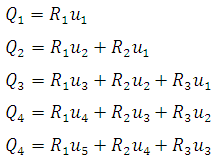
so on

From Eq. 25.1 the values of u₁, u₂, u₃…… can be determined.

 

However, this method suffers from the disadvantage that the errors propagate and increase as the calculations proceed. In the presence of errors the recession limb of the derived D-hunit hydrograph can contain oscillations and even negative values.

 

Example 1

The ordinates of the 6-h unit hydrograph of a basin are given:

Time	h	0	6	12	18	24	30	36	42	48	54	60	66
Ordinate of 6-h UH	m3/s	0	20	60	150	120	90	66	50	32	20	10	0

 

If two storms, each of 1-cm rainfall excess and 6-h duration occur in succession, calculate the resulting hydrograph of flow. Assume the base flow to be uniform at 10m³/s.

 

Answer

C1	C2	C3=C2*1	C4=C2*1	C5= C3+C4	C6	C7= C5+C6
Time	Ordinate of	DRH due to	DRH due to		Base flow	Ordinates of flood
	6-h UH	1. cm ER	1 cm ER			hydrograph
			lagged by 6-h
h	m3/s	m3/s	m3/s	m3/s	m3/s	m3/s
0	0	0		0	10	10
6	20	20	0	20	10	30
12	60	60	20	80	10	90
18	150	150	60	210	10	220
24	120	120	150	270	10	280
30	90	90	120	210	10	220
36	66	66	90	156	10	166
42	50	50	66	116	10	126
48	32	32	50	82	10	92
54	20	20	32	52	10	62
60	10	10	20	30	10	40
66	0	0	10	10	10	20
72			0	0	10	10

 

 

References

Subramanya, K. (2008). Engineering Hydrology.Third edition, Tata McGraw Hill, 212-216.

 

Suggested Reading

Singh, V. P. (1994). Elementary Hydrology.Prentice Hall of India Private Limited,New Delhi.

Murty, V.V.N. and Jha, M.K. (2009).Land and Water Management Engineering.Fifth edition, Kalyani Publishers, Ludhiana.

Suresh R. (2007). Soil and Water Conservation Engineering.Fourth edition, Standard Publishers Distributors, New Delhi.