Site pages
Current course
Participants
General
Module 1. Basic Concepts, Conductive Heat Transfer...
Module 2. Convection
Module 3. Radiation
Module 4. Heat Exchangers
Module 5. Mass Transfer
Lesson 14. Empirical relationships for free and forced convection
Concept of Boundary Layer:
Consider a flat plate over which a fluid is flowing in a direction parallel to the plate. The prevailing flow conditions over the plate have following salient features:
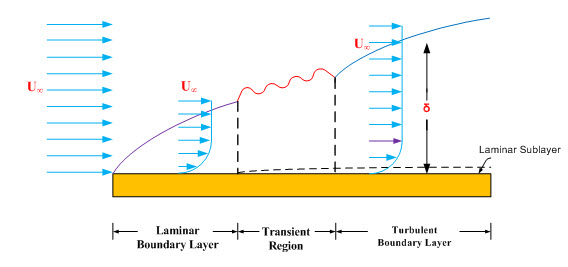
i) As a fluid flows over a solid surface, a layer of fluid coming in contact with solid surface sticks to it due to viscosity. This layer of fluid cannot slip away from the solid surface and attains the same velocity as that of the solid surface. If the solid surface is stationary, the velocity of fluid layer sticking to the surface will be zero. This stationary layer of fluid retards the movement of adjacent layer of fluid resulting in development of a small region near the solid surface in which velocity of fluid increases from zero at solid surface to the velocity of main stream. This region is known as hydrodynamic boundary layer. In this region of boundary layer, there is a large variation in velocity of fluid in a direction normal to the solid surface. Figure 1 shows boundary layer for a fluid flowing over a flat plate.
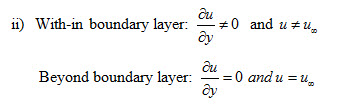
Where u is velocity of flow in boudary layer region and is the free stream velocity.
iii) With the increase in distance from the flat plate in vertical direction, velocity of flow increases and distance at which velocity of flow attains a value of is called thickness of boundary layer denoted by ‘’. Thickness of boundary layer increases with increase in distance from leading edge in flow direction. The growth of boundary layer i.e. thickness is a function of incoming velocity of flow and kinematic viscosity of fluid. At higher incoming velocities, boundary layer growth is suppressed and a higher value of kinematic viscosity of a fluid results in higher value of boundary layer thickness.
iv) Flow with-in the boundary layer is laminar upto certain distance from the leading edge and beyond this distance; flow becomes unstable and becomes transitional in nature. The flow becomes fully turbulent after passing through a transition zone of finite length. Transition from laminar to turbulent flow in boundary layer region is determined by the value of Reynolds number which is expressed as
![]()
Where ‘x’ is distance from leading edge of the plate in flow direction and ‘υ’ is kinematic viscosity.
Laminar flow turns in to turbulent flow in boundary layer region at Reynolds number values between 3*105 to 5*105.
v) For fully turbulent flow in boundary layer region, a laminar sublayer is formed in the immediate vicinity of plate surface where flow is laminar and beyond this sublayer flow is turbulent.
vi) At the plate surface, velocity gradient and shear stress have higher values and along the flow direction these values diminish for laminar boundary layer. However, in turbulent boundary layer, velocity gradient and shear stress have high values near the plate surface.
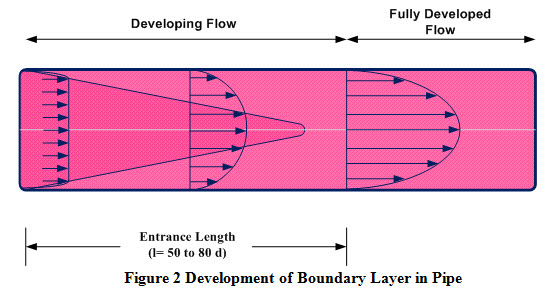
vii) For flow through pipes, boundary layer growth is similar to that over a flat plate except that thickness of the boundary layer is limited to the radius of the pipe as the flow is taking place in an enclosed space. Boundary layer starts developing from pipe walls, meet at the center of pipe and entire flow acquires characteristics of a boundary layer resulting in fully-developed flow. For fully-developed flow, velocity profile is constant; there is no variation in pressure and velocity of flow. The entrance length required for the flow to turn in to fully-developed turbulent flow is a function of fluid properties, initial level of turbulence, downstream conditions and is generally estimated to be 50-80 times the pipe diameter. The velocity distribution for a fully-developed laminar and turbulent boundary layer in a pipe has been shown in Figure 2.
viii) The local skin friction coefficient is defined as ratio of the local wall shear stress to the dynamic pressure of uniform flow.

ix) Depending upon the nature of velocity profile, boundary layer thickness and skin friction coefficient are expressed as

Thermal Boundary Layer:
Similar to hydrodynamic boundary layer, a thermal boundary layer also develops when a fluid flows over a solid surface which is at a temperature different than that of the fluid. Temperature of the fluid layer in contact with the solid surface becomes equal to that of the solid surface. This fluid layer exchanges energy with the adjoining fluid layers resulting in development of region in which temperature variation exists. The region above the solid surface in which temperature variation in the direction normal to the surface exists is called thermal boundary layer. Figure 3 shows thermal boundary layer for a fluid flowing over a solid surface.

The thermal boundary layer thickness ‘’ is defined as the distance from the solid surface in a direction normal to it at which

Where Ts is the temperature of the surface
T∞ is the temperature of fluid outside the thermal boundary layer also called free stream temperature.
‘T is the temperature at a given distance from solid surface with in thermal boundary layer.
At the leading edge of the solid surface, temperature gradient is very high and its value decreases with increase in distance from the solid surface in vertical direction as temperature of fluid approaches free stream temperature. In turbulent boundary layer, formation of eddies decrease the value of temperature gradient.
If the free stream temperature, of the fluid is higher than that of the surface, fluid temperature will be minimum at the surface of the solid and it increases gradually till it becomes equal to the free stream temperature. The vertical distance measured from the surface of the solid to the point where fluid temperature is equal to the free stream temperature denotes the thickness of the thermal boundary layer. Temperature profile in a thermal boundary layer is a function of flow velocity, specific heat, viscosity and conductivity of the fluid. The relationship between thicknesses of hydrodynamic and thermal boundary layers is governed by the Prandtl number value. Prandtl number is expressed as

Thermal boundary layer is thicker than the hydrodynamic boundary layer.
A correlation proposed by Pohlhausen relates Prandtl number with Thermal and hydrodynamic boundary layer thicknesses and is expressed as:
![]()
At the surface of the solid as fluid velocity is equal to zero, the heat flux at the solid surface may be expressed as

Equations (24) and (25) give the local values of convective heat transfer coefficient and Nusselt number at a given distance from the leading edge of the solid surface. Average values of convective heat transfer coefficient and Nusselt number over the entire length, L of the solid surface is given as
