Drainage Engg.2(1+1)

Lesson 13 Salt Balance of Irrigated Land

13.2 Salinisation and Akalisation Problems

Soil salinisation generally refers to the development of salinity in non-salty soil, especially to the development of a non-saline soil into a saline soil. It involves an increase of the soluble salt content of the soil, resulting in an increase of salt concentration of the soil solution. Depending on the salt composition, the ESP may also increase and sodic soils may develop. Sodification almost never occurs in isolation, rather it is usually triggered off by salinisation (Smedema and Rycroft, 1983). Note that salinisation is the basic process underlying the development of almost all salty soils, whether saline or sodic. The problems caused by soil salinity can be grouped into three classes as follows, each class of problem being related to a particular aspect of soil salinity (Smedema and Rycroft, 1983):

(i) Osmotic Problems: They are caused by a high total salt concentration of the soil solution, which raises the osmotic pressure that can be exerted by the soil solution. This makes it more difficult for the plant roots to uptake water from the soil.

(ii) Toxic Problems: They are caused by a high concentration of some particular ion in the soil solution or by the imbalance between two or more ions.  They severely harm plant growth.

(iii) Dispersion Problems: They are caused by relatively high percentage occupancy of the soil exchange complex by Na⁺, which results in poor soil structure due to easy dispersion of the colloids in the soil. They also produce detrimental effects on plant growth.

The detailed discussion of the above salinity problems can be found in Smedema and Rycroft (1983). Salinisation processes discussed in this lesson are those leading to high salinity in the upper soil layers and specifically in the root zone (root-zone salinisation). Two main processes viz., salinisation by irrigation and salinisation by groundwater evaporation are discussed which are related to irrigation, thereby emphasizing the fact that most serious salinisation problems occur in irrigated areas (Smedema and Rycroft, 1983).

13.2.1 Direct Salinisation by Irrigation

All water for irrigation contains some salts. Most irrigation water originates as rainfall which percolates through the soil towards the groundwater and onwards towards the rivers, collecting salts on its way. The use of groundwater for irrigation poses special problems because this water in particular may contain a considerable salt load. This is especially true for arid climates where groundwater is not refreshed so frequently as in humid climates due to low rainfall and high evaporation, and hence salts tend to become more concentrated. Rivers often have a higher salt content during low-flow seasons than during flood seasons. Also, salt conditions may also vary along the course of a river.

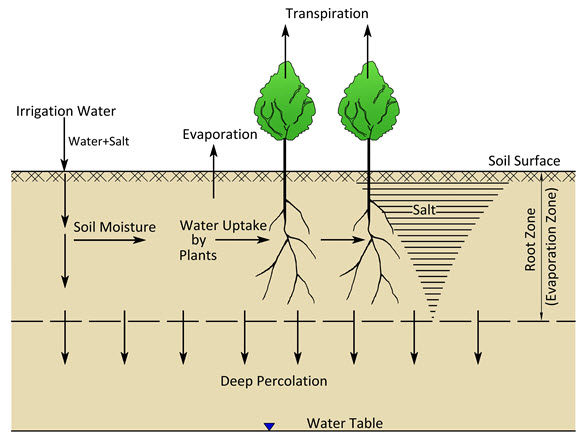
Fig. 13.1. Schematic of direct salinisation by irrigation. (Source: Modified from Smedema and Rycroft, 1983)

Every irrigation event brings a certain amount of salt into the root zone. As the water is lost by evapotranspiration, the salts remain behind in the root zone/evaporation zone (Fig. 13.1) where they will accumulate as is brought in by the irrigation water (salt balance concept) unless an equivalent amount of salt is removed from this zone. The salt uptake by crops is small, salt removal depending almost completely on leaching by deep percolation (i.e., washing out of salt by water percolating through the soil to the depth below the root zone). This type of salinisation is most likely to occur under conditions where the salt influx to the root zone is high and/or the salt outflux from the root zone is low.

High salt influx conditions prevail when the climate is hot and dry (high irrigation water requirements), and the water is saline. On the other hand, low salt outflux conditions prevail when:

• The climate is hot and dry. That is, there are low rainfall and high evaporation, and hence little excess rain goes into deep percolation.

• Minimum irrigation practices are followed, i.e., just enough water is applied to meet the crop evapotranspiration, leaving no excess for deep percolation (i.e., under-irrigation).

• Drainage conditions are poor, which result in insufficient percolation and drainage discharge.

13.2.2 Salinisation by Groundwater Evaporation

Evaporation of saline groundwater from the soil is a common cause of soil salinisation. The groundwater may evaporate directly from the water table when the latters occurs within the evaporation zone, or it may be drawn from deeper down as the evaporation itself will create a gradient for upward capillary flow from the water table into the evaporation zone. It is also known as capillary salinisation. As the water evaporates, the salts remain behind in the evaporation zone (Fig. 13.2). Hence, this type of salinisation takes place only when saline groundwater occurs within such a depth that upward capillary flow is able to reach the evaporation zone.

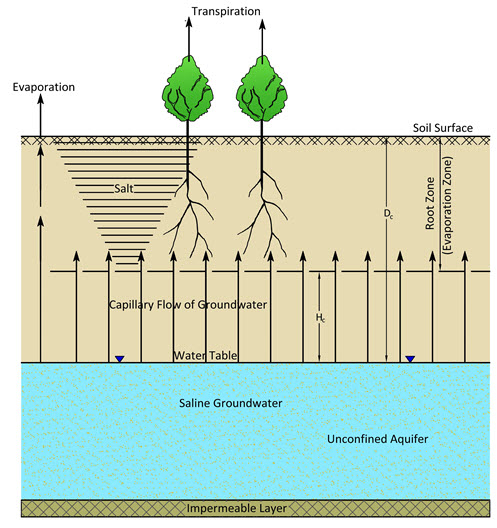
Fig. 13.2. Schematic of capillary salinisation. (Source: Modified from Smedema and Rycroft, 1983)

A great deal of irrigated land is underlain at shallow depth by saline groundwater. Prior to the introduction of irrigation, groundwater recharge is usually low, consisting only of deep percolation due to rainfall which is also low under the arid climatic setting of a typical irrigation scheme. In general, the natural groundwater discharge can easily cope with such a low recharge, even with deep water tables (low head). The deep percolation component of the irrigation can in some cases (permeable soil, poor irrigation practices and management) amount to 20-30% of the irrigation water supplied and recharge under irrigation can easily rise to a multiple of the original recharge. Water tables will rise up to a level which produces sufficient hydraulic head for the required higher discharge. There are numerous irrigation projects where this has happened with water tables rising from 20-30 m depth to 1-2 m depth below the soil surface during a period of 10-15 years the start of the project (Smedema and Rycroft, 1983).

13.2.3 Critical Water Table Depth

Capillary flow upwards from a water table can reach to great heights but the rate of flow generally decreases with increasing height above the water table. So the rate of upward salt movement, being proportional to the rate of upward flow, also decreases as the distance between the evaporation zone and the water table increases (Fig. 13.3). The distance at which the upward capillary flow becomes too small for any significant upward salt movement is called critical capillary height (H_c). Its value depends on following two factors (Smedema and Rycroft, 1983):

(a)   Soil type: Soils with a large proportion of their pores of a small size, have large H_c values (e.g., fine sandy loam, silty loam). Coarse sand has a small H_c value, whereas well structured medium to fine soils have intermediate values (Fig. 13.3).

(b)   Salt concentration of groundwater: Upward salt movement is the product of ‘Flow rate’ ´ ‘Salt concentration’. Therefore, H_c values should increase with increasing groundwater salinity (Fig. 13.4). In general, very little capillary salinisation will occur provided the salt concentration in the upper groundwater layer remains <1000 mg/L (EC £ 1.5 mmhos/cm).

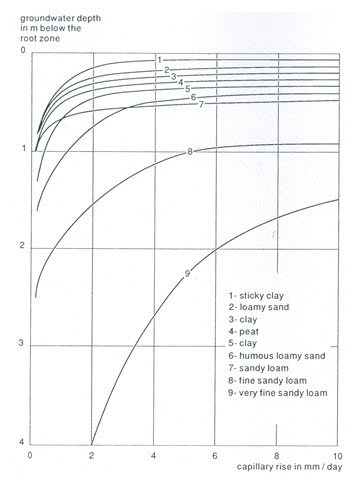
Fig. 13.3.  Capillary rise of groundwater to the root zone for different groundwater depths and soil textures under moist conditions (soil water tension in the root zone » 5 m). (Source: Doorenbos and Pruitt, 1977)

In situations where the groundwater inflow or outflow in the area is insignificant, the critical water table depth (D_c) may be estimated as the depth to which the water table falls towards the end of a long dry period. Some indicative values for H_c are given in Table 13.1 (Smedema and Rycroft, 1983):

Table 13.1. Indicative values of critical capillary heights for selected soils

Sl. No.	Type of Soil	Critical Capillary Height (Hc)
1	Sand (Coarse ® Fine)	Hc = 50 ® 75 cm
2	Loamy Sand, Sandy Loam	Hc = 100-150 cm
3	Fine Sandy Loam, Silt Loam	Hc =150-200 cm
4	Loam, Clay Loam, Clay	Hc =100-150 cm

The values given in Table 13.1 apply to uniform soil profiles. The stratification of soils generally reduces the high values, but it may increase the low values.

Fig. 13.4. Interaction between critical water table depth and salt concentration of groundwater in Lower Indus, Pakistan. (Source: Smedema and Rycroft, 1983)

13.2.4 Sodification

Sodification (also known as ‘Alkalisation’) involves the replacement of other cations on the adsorption complex by sodium. Significant replacement only occurs when Na⁺ becomes the dominant soluble cation in the soil solution (high SAR-value). This may occur when the salinizing source is Na⁺ rich, when the soil solution becomes more concentrated or when for other reasons the salinisation processes favour the accumulation of Na⁺. The presence of CO₂^{- -} and HCO₂^- in the soil solution is especially important. These anions form salts with Ca⁺⁺ which are only slightly soluble while the corresponding Na⁺ salts are highly soluble. Their presence thus leads to a relative enrichment of the soil solution with Na⁺ as the overall salt concentration increases because the Ca⁺⁺ salts precipitate.

Sodic soils, having a low concentration of salts in the soil solution but a high Na⁺ occupancy on the complex also occur. The high values of ESP that these soils exhibit are unlikely to have developed under conditions of low salinity. In fact, these soils almost aways develop from saline-sodic soils by a leaching process in which the soluble salt concentration of the soil decreases more rapidly than the Na⁺ occupancy on the complex.

13.3 Salt Balance of Irrigated Land

13.3.1 Dynamic Salt Balance Equation

The salt balance for a root zone under irrigation (Fig. 13.5) can be expressed as:

Where, I = irrigation water entering the root zone, C_i = salt concentration of the irrigation water, P_e = effective precipitation (i.e., precipitation entering the root zone), C_p = salt concentration of the rainwater, GW = groundwater inflow into the root zone (i.e., capillary flow into the root zone), C_gw = salt concentration of the groundwater, DP = deep percolation from the root zone, C_dp = salt concentration of the deep percolated water, and DS = change in salt content of the soil solution in the root zone.

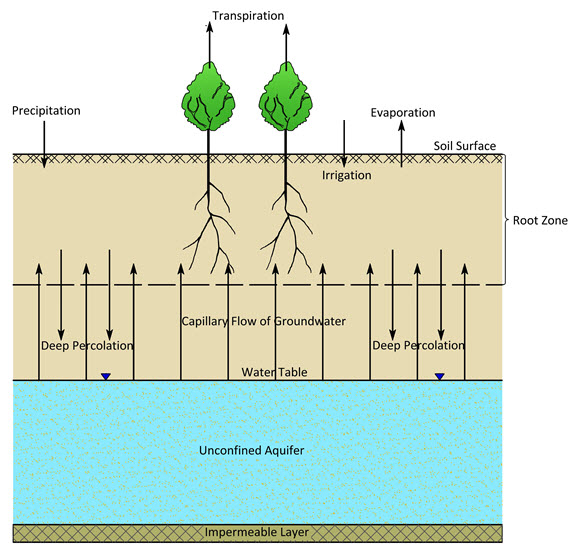
Fig. 13.5. Water balance of an irrigated land. (Source: Modified from Smedema and Rycroft, 1983)

I, P, GW and DP may be expressed in various units although mm/period is most convenient (e.g., mm/month, mm/season, etc). The correct unit for salt concentration is mg/L, but since C and EC are linearly related mhos/cm may also be used. Note that Eqn. (13.1) applies to the soluble salts only. It should also be noted that this equation ignores some of the components of the more detailed salt balance relation given by Rhoades (1974). The salt balance components which have been ignored are: the salt input due to weathering of soil mineral, salt input through fertilisers and amendments, temporarily precipitated salt input from irrigation water that may re-dissolve, and the salt output through uptake by the plants. All these salt balance components are much smaller than the other components and their elimination from the detailed salt balance relation is justified for field works on drainage and land reclamation. For example, the salt uptake by common crops can be either neglected or assumed to be offset by the fertilizer application (Smedema and Rycroft, 1983).

13.3.2 Leaching Requirement

Equation (13.1) reduces to Eqn. (13.2) under the following conditions (Smedema and Rycroft, 1983):

(i) C_p is negligible small as is the case for normal rainwater which has an EC-value of 0.02-0.05 mmhos/cm; close to the seawater, however, the salt content of the rainwater may rise to EC = 0.20-0.30 mmhos/cm.

(ii) C_gw = C_dp, a reasonable assumption for averages over annual periods; less valid for short time periods.

(iii) DS = 0, i.e., the salt balance is in equilibrium (i.e., salt contents in the root zone at the beginning of the period and at end are equal).

The assumption of DS = 0 means that there is no change in the salt content of the soil solution from what it was at the beginning of the period under consideration to what it is at the end of the period. If the period considered is one irrigation season, it implies that inter-seasonally, there is neither a cumulative salt build up nor a cumulative salt depletion from the soil depth (root zone) under consideration. This assumption tends to be more justified over a long period such as a season or a year. The assumption of equality of the salt concentration of the groundwater and deep percolated water is also reasonably valid in terms of their average values over a long period. However, the above assumptions are grossly violated during short time periods such as day or week.

Where, LR = leaching requirement, which is the excess of deep percolation over groundwater inflow into the root zone (GW).

Note that when a water quantity LR satisfying Eqn. (13.2) is drained from the root zone, as much salt is leached from the root zone as is brought in by the irrigation. Eqn. (13.2b) can be rewritten as follows:

 

Equation (13.3) expresses LR as a fraction of I, i.e., the fraction of the infiltrated irrigation water that must go into deep percolation in order to maintain a salt balance in the root zone. Thus, leaching requirement (LR) is a fraction of the amount of irrigation water and the fraction is the ratio of the salinity of the irrigation water to the salinity of the deep percolated (drained) water. The fractional factor  is called the leaching fraction or leaching percentage when expressed as  .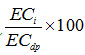

It is obvious from Eqn. (13.3) that for a given irrigation water quality (EC_i), the leaching requirement will increase if the deep percolated water electrical conductivity (EC_dp) is to be decreased. Under real-world conditions, EC_i is always less than EC_dp. Hence, their ratio is always less than 1. In a hypothetical situation, when there is no salts present in the soil solution in the excess of the salt concentration of the irrigation water, LR and I becomes equal. This means that there is no requirement of water in excess of irrigation requirement for the purpose of leaching. However, in the actual field situation, since the salt concentration of the soil solution is higher than the salt concentration of irrigation water, the actual quantity of water to be applied for both irrigation and leaching will be the sum of LR and the irrigation water requirement (I), i.e.,

 

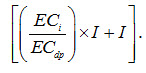
Moreover, in an equilibrium situation, the following water balance also holds (Fig. 13.5):

 

In this equation, (ET-P_e) is the rainfall deficit (i.e., Net crop irrigation requirement, designated as I_c), while the difference (DP-GW) represents the leaching requirement (LR). Thus, Eqn. (13.4) can be written as:

Where, I is called total irrigation requirement (i.e., Net crop irrigation requirement + Leaching requirement). Combining Eqns. (13.3) and (13.5) yields:

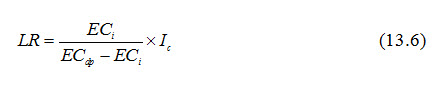
The required LR can be calculated using Eqn. (13.6), if the values of EC_i and I_c are known and a value of EC_dp is selected on the basis of an acceptable level of salinity in the root zone.

13.3.3 Computation of Leaching Requirement

Values for EC_dp should be determined experimentally by sampling the soil below the root zone (the upper groundwater or the drain water). In planning, the values of EC_dp are usually set equal to the maximum salinity which can be tolerated in the root zone. On the basis of certain considerations to deal with complex flow and salt transport in the root zone, the values for EC_dp in Eqn. (13.6) are often taken as (Rhoades, 1974):

• EC_dp = 2EC_e25% in cases where crops are mostly sensitive, or rather low leaching efficiencies are to be expected or where a high standard of salinity control is desirable.

• EC_dp = 2EC_e50% in cases where crops are more tolerant to salinity, or high leaching efficiencies are to be expected or a somewhat lower salinity control is considered acceptable.

The value of EC_e25% and EC_e50% can be obtained from the standard table given in FAO (1976).

Example Problem: Calculate LR, total irrigation requirement (I) and leaching percentage (LP) for the following data (Smedema and Rycroft, 1983):

EC_i = 1.2 mmhos/cm, EC_dp = 12.0 mmhos/cm (= 2 ´ EC_e50% for the crop to be grown), and I_c = 6 mm/day.

Solution:

We know that

This example shows the salt balance in the root zone is maintained when a minimum of 10% of the infiltrated irrigation water goes as deep percolation. A deep percolation loss of this order or even higher is quite common under surface irrigation methods, and hence there is generally no need to over-irrigate to satisfy the leaching requirement (Smedema and Rycroft, 1983).

13.3.4 Regional Salt Balance

The basic principle of the salt balance discussed above can also be applied regionally as follows:

Salt Influx in a Region - Salt Outflux from the Region = Change in Salt Storage in the Region        (13.7)

The salt influx or outflux can be calculated as: Water flux ´ Salt concentration ´ Time. Both the water flux and the salt concentration vary during the year. Therefore, annual fluxes have to be determined by summing the assumed uniform salt fluxes occurring during shorter periods of time. Dimensional units could be m³/s or mm/day for the water flux and g/L, ppm or mmhos/cm for the salt concentration.

The water fluxes in a region, especially those due to groundwater, are very difficult to quantify. Hence, we often have to rely on estimates (Smedema and Rycroft, 1983). If water inflows into and outflows from regions are denoted by Q_i and Q_d, respectively and their salt concentrations are denoted by C_i and C_d, the regional salt balance equation can be written as follows:

 

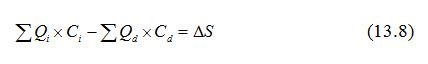
Equation (13.8) can be used to examine whether in the long term salts are likely to accumulate in a region (e.g., irrigated area).

References

Doorenbos, J. and Pruitt, W.O. (1977). Guidelines for Predicting Crop Water Requirements. FAO Irrigation and Drainage Paper 24, Food and Agriculture Organization (FAO), Rome, Italy.

FAO (1976). Water Quality for Irrigation. Irrigation and Drainage Paper 29, Food and Agriculture Organization (FAO), Rome, Italy.

Rhoades, J.D. (1974). Drainage for Salinity Control. In: J. van Schilfgaarde (Editor), Drainage for Agriculture, Agronomy Monograph 17, American Society of Agronomy, Madison, Wisconsin.

Smedema, L.K. and Rycroft, D.W. (1983). Land Drainage: Planning and Design of Agricultural Drainage Systems. Batsford, London.

USDA (1954). Diagnosis and Improvement of Saline and Alkali Soils. Agricultural Handbook No. 60, US Department of Agriculture, Washington DC.

Suggested Readings

Bhattacharya, A.K. and Michael, A.M. (2003). Land Drainage: Principles, Methods and Applications. Konark Publishers Pvt. Ltd., New Delhi, India.

Murty, V.V.N. and Jha, M.K. (2011). Land and Water Management Engineering. Sixth Edition, Kalyani Publishers, Ludhiana, India.

Smedema, L.K. and Rycroft, D.W. (1983). Land Drainage. Batsford Academic and Education Ltd., London.

Ritzema (Editor-in-Chief) (1994). Drainage Principles and Applications. International Institute for Land Reclamation and Improvement (ILRI), ILRI Publication 16, Wageningen, The Netherlands.

Schwab, G.O., Fangmeier, D.D., Elliot, W.J. and Frevert, R.K. (2005). Soil and Water Conservation Engineering. Fourth Edition, John Wiley and Sons (Asia) Pte. Ltd., Singapore.