System Engineering 3(3+0)

LESSON 3. Assignment problems - Assignment algorithm

Assignment Algorithm (or) Hungarian Method

First check whether the number of rows is equal to the number of columns, If it is so, the assignment problem is said to be balanced.  Then proceed to step 1.  If it is not balanced, then it should be balanced before applying the algorithm.

Step 1: Subtract the smallest cost element of each row from all the elements in the row of the given cost matrix.  See that each row contains atleast one zero.

Step 2: Subtract the smallest cost element of each column from all the elements in the column of the resulting cost matrix obtained by step 1.

Step 3: (Assigning the zeros)

(a)    Examine the rows successively until a row with exactly one unmarked zero is found.  Make an assignment to this single unmarked zero by encircling it. Cross all other zeros in the column of this encircled zero, as these will not be considered for any future assignment.  Continue in this way until all the rows have been examined.

(b)   Examine the columns successively until a column with exactly one unmarked zero is found.  Make an assignment to this single unmarked zero by encircling it and cross any other zero in its row.  Continue until all the columns have been examined.

Step 4: (Apply optimal Test)

(a) If each row and each column contain exactly one encircled zero, then the current assignment is optimal.

(b) If atleast one row/column is without an assignment (i.e., if there is atleast one row/column is without one encircled zero), then the current assignment is not optimal.  Go to step 5.

Step 5: Cover all the zeros by drawing a minimum number of straight lines as follows.

(a) Mark (√) the rows that do not have assignment.

(b) Mark (√) the columns (not already marked) that have zeros in marked rows.

(c) Mark (√) the rows (not already marked) that have assignments in marked columns.

(d) Repeat (b) and (c ) until no more marking is required.

(e) Draw lines through all unmarked rows and marked columns.  If the number of these lines is equal to the order of the matrix then it is an optimum solution otherwise not.

Step 6: Determine the smallest cost element not covered by the straight lines.  Subtract this smallest cost element from all the uncovered elements and add this to all those elements which are lying in the intersection of these straight lines and do not change the remaining elements which lie on the straight lines.

Step 7: Repeat step (1) to (6), until an optimum assignment is attained.

Problem: 

A works manager has to allocate four different jobs to four workmen.  Depending on the efficiency and the capacity of the individual the times taken by each differ as shown in the Table 1.  How should the tasks be assigned one job to a worker so as to minimize the total man-hours?

Table   1

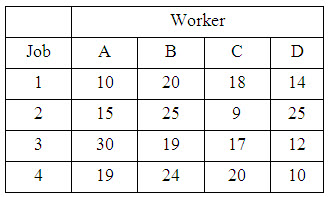
Solution: 

The following steps are followed to the find an optimal solution.

STEP  1

Consider each row.  Select the minimum element in each row.  Subtract this smallest element form all the elements in that row.  This results in the table 2.

Table   2

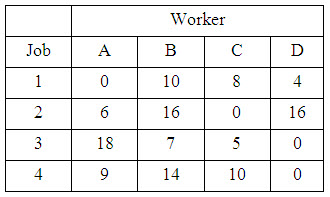
STEP   2 

Subtract the minimum element in each column from all the elements in its column.  This will result in Table 3.

Table   3

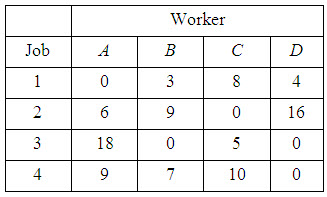
STEP   3

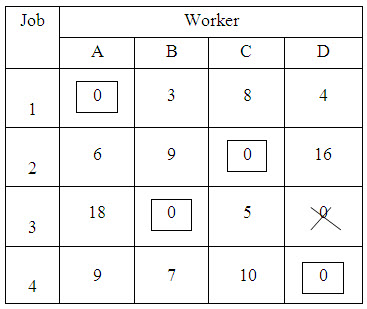
In this way we make sure that in the matrix each row and each column has atleast one zero element.  Having obtained atleast one zero in each row and each column, we assign starting from first row.  In the first row,  we have a zero in (1,A).  Hence we assign job 1 to the worker A.  This assignment is indicated by a square. All other zeros in the column are crossed (X) to show that the other jobs cannot be assigned to worker A, who  has already been assigned.   In the above problem we do not have other zeros in column A.

Proceed to the second row where there is  a zero in (2,C) .  Hence  the job 2 can be assigned  to worker C, indicating by a square.  Any other zero in this column is crossed (X).

Proceed to the third row. Here we have two zeros corresponding to (3,B) and (3, D).  Since there is a tie for the job 3, go to the next row deferring the decision for the present.  Proceeding to the fourth row, there IS only one Zero in (4, D).  Hence assign job 4 to worker D.  Now the column D has a zero in the third row and cross (3, D).  All  the assignments made in this way are as shown in Table 4.

Table 4

 

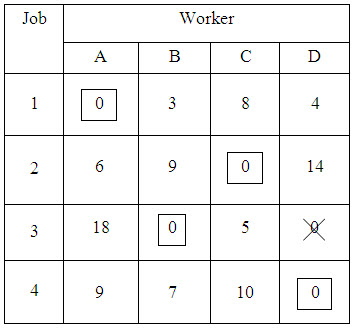
STEP  4

Now having assigned certain jobs to certain workers we proceed to the column 1.  Since there is an assignment in this column,  we proceed to the second column.  There is only one zero in the cell (3, B);  We assign the jobs 3 to worker B.  Thus all the four jobs have been assigned to four workers.  Thus we obtain the solution to the problem as shown in the Table 5

Table 5

 

 

The assignments are

 

The above procedure is summerised as a set of following rules: 

1. Subtract the minimum element in each row from all the elements in its row to make sure that at least there is one zero in that row.

2. Subtract the minimum element in each column from all the elements in its column in the above reduced matrix, to make sure that  atleast one zero exists in each column.

3. Having obtained atleast one zero in each row and atleast one zero in each column, examine rows successively until a row with exactly one unmarked zero is found and mark (X) this zero, indicating that assignment in made there.  Mark (X) all other  zeros in the same column, to show that they cannot be used to make other assignments.  Proceed in this way until all rows have been examined.  If there is a tie among zeros defer the decision.

4. Next consider columns, for single unmarked zero, mark them (   ) and mark (X) any other unmarked  zero in their rows.

5. Repeat (c) and (d) successively until one of the two occurs

(1)    There are no zeros left unmarked.

(2)    The remaining unmarked zeros lie atleast two in each row and column.  i.e., they occupy corners of a square.

If the outcome is (1), we have a maximal assignment.  In the outcome (2) we use arbitrary assignments.  This process may yield multiple solutions.

Solving problem following Hungarian Method

Problem:

Building	Contractor
	1	2	3	4
A	48	48	50	44
B	56	60	60	68
C	96	94	90	85
D	42	44	54	46

Solve the following assignment problem to minimize the total cost represented as elements in the matrix (cost in thousand rupees).

 

 

 

 

Solution:

STEP 1:

	Contractor
Building	1	2	3	4
A	4	4	6	0
B	0	4	4	12
C	11	9	5	0
D	0	2	12	4

Choose the least element in each row of the matrix  and subtract the same from all the elements in each  row so that each row contains atleast one zero.  This results in Table 6

 

 

 

 

 Table 6                          

 

STEP  2:

Choose the least element from  each column in Table 6 and subtract the same form all the elements in that column to ensure that there is atleast one zero in each column.  This results in the following table (Table 7)

Table 7

 

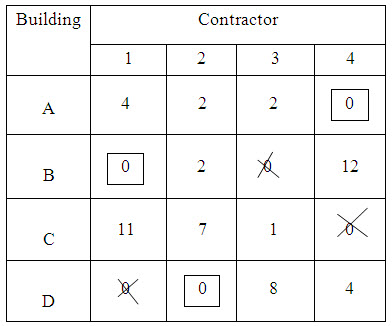
STEP  3:

Make the assignment in each row and column  as explained previously.  This results in table 8

Table 8

 

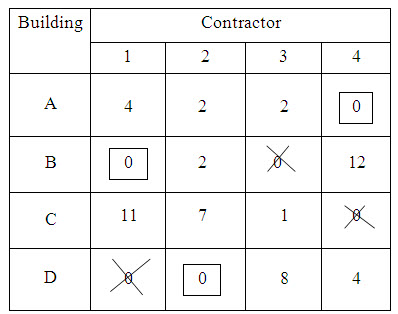
Here there are only three assignments, but  four assignments are required.  With this maximal assignment, minimum number of lines to cover all the zeros are needed to draw.  This is carried out as explained in steps 4 to 9.  Refer Table 9

Table 9

 

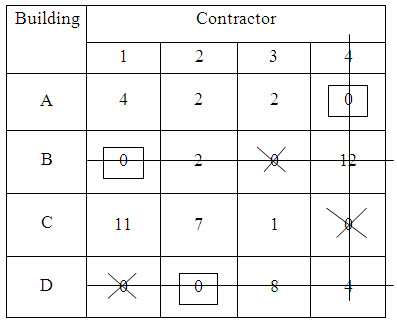
STEP  4:

            Mark ( X ) the unassigned row (row C).

STEP  5:

            Against the marked column 4, look for any (X) element and mark that column (column 4).

STEP  6:

            Against the marked column 4, look for any assignment and mark that row (row A.)

STEP  7:

            Repeat steps 6 and 7 until the chain of markings ends.

STEP  8:

            Draw lines through all unmarked rows (row B and Row D) and through all marked columns (column 4).  (Check:  There should be only three lines to cover all the zeros).

STEP  9:

Select the minimum from the elements that do not have a line through them.  In this example we have 1 as the minimum element, subtract the same from all the elements that do not have a line through them and add this smallest element at the intersection of two lines.  Thus we have the matrix shown in Table 10

Table 10

 

 

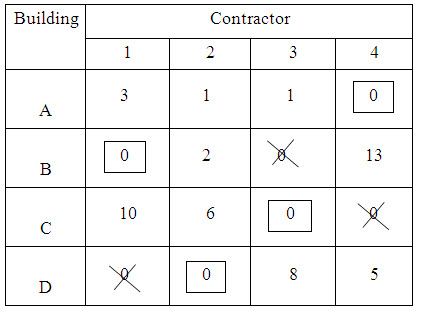
STEP  10:

            Go ahead with the assignment with the usual procedure.  This is carried out in the Table 10.  Thus we have four assignments.

            Building A is allotted to contractor 4

Building B is allotted to contractor 1

Building C is allotted to contractor 3

Building D is allotted to contractor 2

Total cost is 44 + 56 + 90 + 44 = Rs.234 thousands.

Example 2

There are five machines and five jobs are to be assigned and the associated cost matrix is as follows. Find the proper assignment.

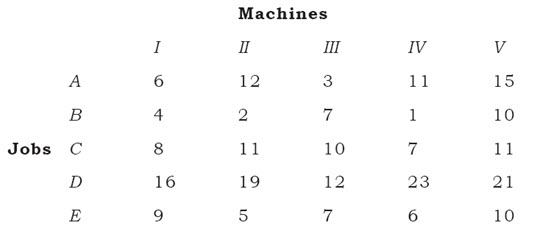
Solution:

In order to find the proper assignment, we apply the Hungarian  method as follows:

Step 1: Row reduction

 

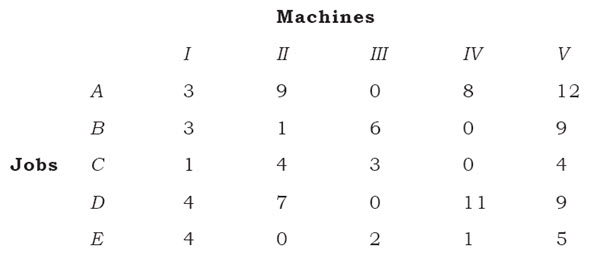
Step 2: (Column reduction)

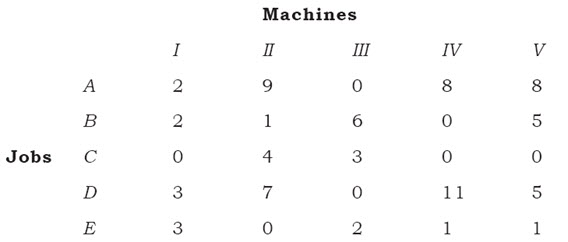
Step 3: (Zero Assignment)

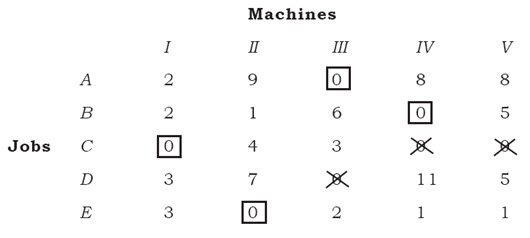
From the last table we see that all the zeros are either assigned or crossed out, but the total number of assignment,i.e., 4<5 (number of jobs to be assigned to machines). Therefore, we have to follow step 4 and onwards as follows:

Step 4:

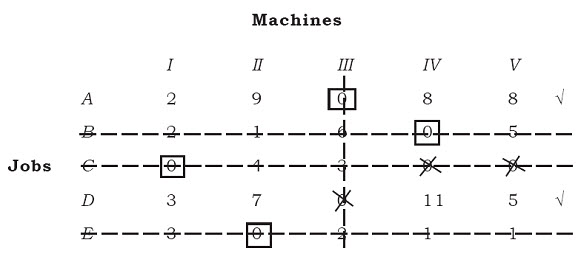
Step 5:

Here, the smallest element among the uncovered elements is 2.

(i)             Subtract 2 from all those elements which are not covered.

(ii)           Add 2 to those entries which are at the junction of two lines.

Complete the table as under:

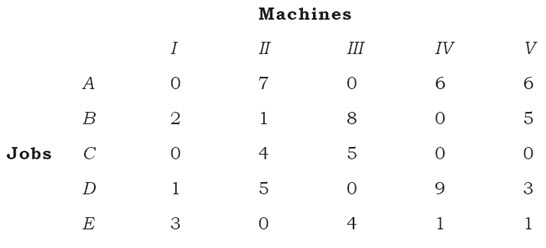
Step 6: using step 3 again

 

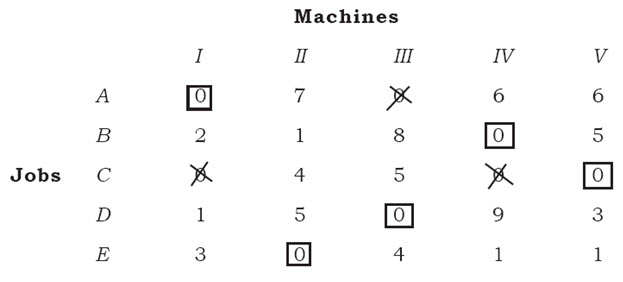
Thus, we have got five assignments as required by the problem.

The assignment is as follows:

 

Thus from the cost matrix the minimum cost = 6+1+11+12+5=Rs.35.

Note:

If we are given a maximization problem then convert it into minimization problem, simply, multiplying by -1 to each entry in the effectiveness matrix and then solve it in the usual manner.