Strength of Material 3(2+1)

LESSON 1. Analysis of Statically Determinate Beams

1.2 Degrees of Freedom (DOF)

The degree of freedom of a mechanical system is the number of independent coordinates required to completely specify the configuration of the system. Motion of an object in a three-dimensional space can be completely described by three displacements (along three coordinate axes) and three rotations (about three coordinate axes) as shown in Figure 1.1a. Therefore in three-dimensional space an object has six degrees of freedom. Similarly in two dimensional plane an object has three degrees of freedom viz. two displacements along two coordinate axes and one rotation about an axis normal to the plane as shown in Figure 1.1b.

Fig. 1.1.

1.3 Force

To solve typical structural problems, we use equations involving forces or their components. Forces may consist of either a linear force that tends to produce translation or a couple that tends to produce rotation of the body on which it acts.

A system of planner forces acting on a rigid structure can always be reduced to two resultant forces (see Figure 1.2):

(a) A linear force R passing through the centre of gravity of the structure where R equals the vector sum of the linear forces.

(b) A moment M about the centre of gravity. The moment M is evaluated by summing the moments of all forces and couples acting on the structure with respect to an axis through the centre of gravity and perpendicular to the plane of the structure.

 

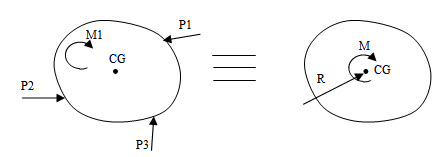
Fig. 1.2.

1.4 Supports and Support Reaction

To ensure that a structure or a structural element remains in its required position under all loading conditions, it is attached to a foundation or connected to other structural members by supports. Support constraints the motion of a structure by exerting resistive force called Support reaction. Depending on the number and type of constraints there are different kinds of supports. Characteristics of different kinds of supports in two-dimensions are summarized in Table 1.1.

Table 1.1 Support characteristics

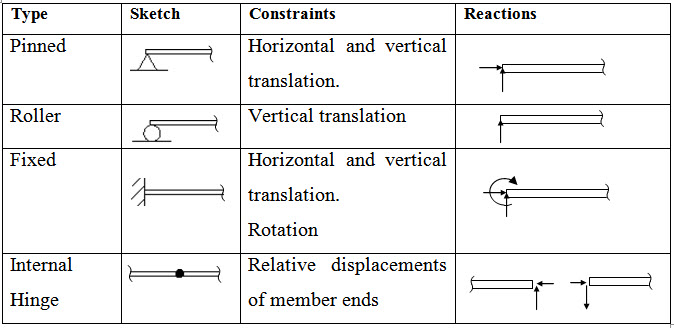
1.5 Free Body Diagram

As a first step in the analysis of a structure, we draw a simplified sketch of the structure or a portion of the structure under consideration. A free body diagram is a pictorial device used in order to analyze the forces and moments acting on a body. This sketch, which shows the required dimensions together with all the external and internal forces acting on the structure is called free-body diagram (FBD). For instance Figure 1.3b shows the free-body diagram of the entire structure of a simply supported beam subjected to concentrated load at its midspan (Figure 1.3a). Let the beam is cut by a section mn. Figure 1.3c shows the free body diagram of the portion of the beam to the left part of the section mn.

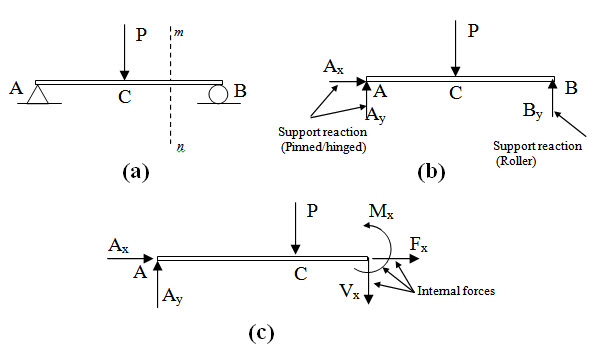
Fig. 1.3.

1.6 Equations of Static Equilibrium

An object at rest is said to be in static equilibrium if the net forces acting on the body is zero. In three dimensions the equations of static equilibrium are as follows,

\[\sum {{F_x}=0}\] ; \[\sum {{F_y}=0}\] ;  \[\sum {{F_z}=0}\]           [Net force in any direction is zero]

\[\sum {{M_x}=0}\] ;  \[\sum {{M_y}=0}\] ;  \[\sum {{M_z}=0}\]      [Net moment about any axis is zero]

Similarly in two dimensions the above equations become,

\[\sum {{F_x}=0}\] ;     \[\sum {{F_y}=0}\]                          [Net force in any direction is zero]

        \[\sum {{M_z}=0}\]                                    [Net moment about any axis is zero]

1.7 Determinate and Indeterminate Structure

A structure is said to be determinate if the equations of static equilibrium alone are sufficient to permit a complete analysis of the structure. If the structure cannot be analyzed by the equation of statics, the structure is termed as indeterminate. To analyze an indeterminate structure, additional equations considering the geometry of the deflected shape are required. This will be discussed in details in the next module. In this module we will learn several methods to analyze statically determinate beams.

Suggested Readings

Hbbeler, R. C. (2002). Structural Analysis, Pearson Education (Singapore) Pte. Ltd.,Delhi.

Jain, A.K., Punmia, B.C., Jain, A.K., (2004). Theory of Structures. Twelfth Edition, Laxmi Publications. 

Menon, D.,  (2008), Structural Analysis, Narosa Publishing House Pvt. Ltd., New Delhi.

Hsieh, Y.Y., (1987), Elementry Theory of Structures , Third Ddition, Prentrice Hall.