Engineering Mechanics 3(2+1)

LESSON 3. PRINCIPLE OF SUPERPOSITION OF FORCES

Fig. 3.1 Principle of superposition

3.2 COUPLE

A system of two equal parallel forces acting in opposite directions is said to form a couple. Fig.3.2 shows a couple formed by horizontal, vertical and inclined forces.

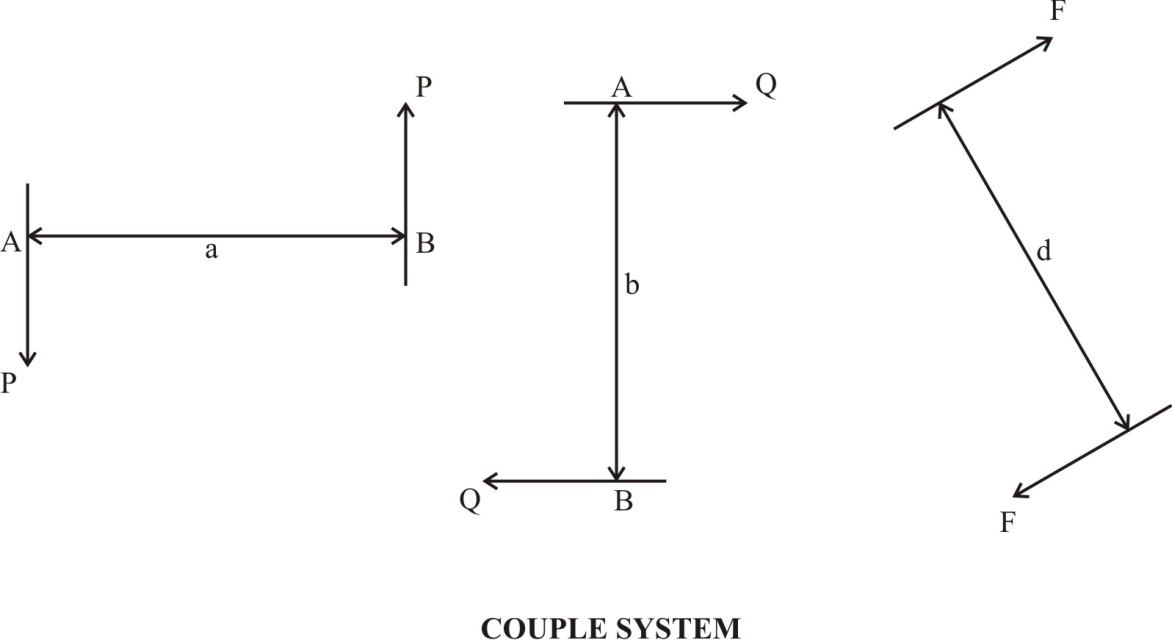
Fig. 3.2 Couple systems

The plane in which the two forces forming a couple lie is called the plane of the couple and the distance between their line of action is called the arm of the couple. Any couple acting on a rigid body produces only rotation to the body. This rotation is measured by the moment of the couple, which is product of magnitude of the force and the distance between the two forces (arm of the couple). In contrast, the couple does not cause any translation to the rigid body.

The magnitude of the moment of the couple is determined by using the principle of superposition. That is, the moment of the couple is equal to the sum of the moment of the two forces of the couple about any point. As seen in Fig.3.3, the moment of couple about O₁ is given by

M_O1 = +F(d₁) – F(a+d₁) = -F × a                                                                                      (2.1a)

Similarly, the moment of the couple about point O₂ is

M_O2 = -F(a-d₂) – F(d₂) = -F × a                                                                                        (2.1b)

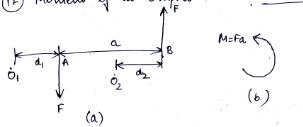
Fig.3.3 Moment of  a couple

It is clear that the moment of a couple about any point is always constant. Interestingly, couple can also be diagrammatically shown by a rotation arrow as shown in Fig.3.3(b) indicating the magnitude of the moment of a couple, M = Fa.

3.2.1 Characteristics of a Couple

A couple is completely defined by following elements:

i) The magnitude of its moment

ii) The plane in which it acts defined by the direction of the normal to the plane.

iii) The direction of rotation in the plane that is the sense of the couple.

Moment of a couple is a vector quantity having the direction normal to the plane in which it acts.

3.3 EQUIVALENT FORCE-COUPLE SYSTEM

A force at any given point on a rigid body can always be replaced by another force of same direction but acting at different point along with an associated couple.

Let P be a force acting on a rectangular plane at point A as shown in Fig.3.4(a). Introducing two collinear forces of magnitude P acting opposite to one another at point B and parallel to the one acting at A as indicated in fig. 12(b), the condition remain same as in Fig.3.4(a) itself. According to the principle of superposition, the systems shown in Fig.3.4(a) and (b) are statically equivalent. Subsequently, the force P acting at A and the one acting at B opposite to that at A can be combined together to form a couple, the moment of which is M = Pa acting in counter-clockwise direction [see fig. 3.4(c)]. This couple can be applied at any point on the plate and is shown in fig. 3.4(a) is statically equivalent to the force-couple system shown in Fig. 3.4. This indicates that any given force can be reduced into an equivalent force-couple system and vice versa.

 

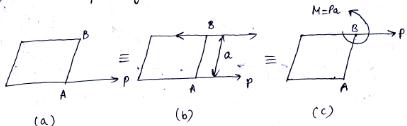
Fig.3.4 Force-couple system