Engineering Mechanics 3(2+1)

LESSON 5. SYSTEM OF FORCES

5.2 EQUILIBRIUM OF FORCES

Equilibrium is defined as the condition of a body, which is subjected to a force system whose resultant force is equal to zero. It means the effect of the given force system is zero and the particle or rigid body is said to be in equilibrium.

For example, a particle subjected to two forces will be in equilibrium when the two forces are equal in magnitude, opposite in direction and act along the same line of action as shown in Figure.

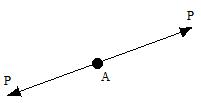
Fig. 5.1 Equilibrium of forces

5.2.1 Equations of equilibrium for a concurrent, coplanar force system

The resultant of a concurrent, coplanar force system is a single force through the point of concurrence. When the resultant force is zero, the body on which the force system acts in equilibrium.

Consider the force system as shown in figure:

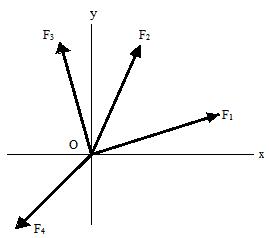
Fig.5.2 Equilibrium of concurrent and coplanar Force system

If the sum of the x components of the forces of the system is equal to zero, the resultant can act only along the y axis.

If in addition, the sum of the y components of the forces of the system is equal to zero, the resultant must be zero. Consequently, one complete set of equations of equilibrium for a concurrent, coplanar force system is

∑ F_x = 0,   ∑ F_y = 0                          (5.1)                

Again, if the sum of the x components of the forces of the system is equal to zero, the resultant can be only a force along the y axis and if the sum of the moments of the forces of the system with respect to an axis through A is equal to zero where A is any point not on the y axis is not zero. Thus, another set of equations which assure equilibrium for this system is

∑ F_x = 0,    ∑ M_A = 0                                                                                        (5.2)

Where A is not on the y axis.

In a similar manner, a third set of independent equations can be shown to be

∑ M_A = 0,    ∑ M_B = 0                                                                                      (5.3)

Where line AB does not pass through the point of concurrence of the forces of the system. There are only two independent equations of equilibrium for a concurrent, coplanar force system. When a force system of this type contains not more than two unknowns (two magnitudes, one magnitude and one slope, or two slopes), they can be determined directly from the equations of equilibrium.

When a concurrent, coplanar force system contains more than two unknowns, they cannot all be determined from the equations of equilibrium alone, and the force system is said to be statically indeterminate.

For a collinear force system, Eq.(5.1) reduces to one equation,

∑ F_x = 0

Where the x axis is parallel to the forces. Likewise, Eq.(5.2) can be reduced to the equation

∑ M_A = 0