Engineering Mechanics 3(2+1)

LESSON 6. General Procedure for the solution of problems in Equilibrium

6.1.1 Step by Step Procedure

1. Determine carefully what data are given and what results are required.

2. Draw a free body diagram of the member or group of members on which some or all of the unknown forces are acting.

3. Observe the type of force system which acts on the free body diagram drawn.

4. Note the number of independent equations of equilibrium available for the type of force system involved.

5. Compare the number of unknowns on the free body diagram with the number of independent equations of equilibrium available for the force system.

6. (a) If there are as many independent equations of equilibrium as unknowns, proceed with the solution by writing and solving the equations of equilibrium.

    (b) If there are more unknowns to be evaluated than independent equations of equilibrium available, draw a free body diagram of another body and repeat steps 3,4 and 5 for the second free body diagram drawn.

7. (a)If there are as many independent equations of equilibrium as unknowns for the second free body diagram, proceed with the solution by writing and solving the necessary equations of equilibrium.

    (b) If there are more unknowns to be evaluated than independent equations of equilibrium for the second free body diagram, compare the total number of unknowns on both free body diagrams with the total number of independent equations of equilibrium available for both diagrams.

8. If there are as many independent equations of equilibrium as unknowns for both diagrams, proceed to solve the problem by writing and solving the equations of equilibrium. If there are more unknowns than independent equations of equilibrium, repeat step 6(b) and 7. If there are still too many unknowns after as many free body diagrams have been drawn as there are individual bodies in the problem, then the problem is statically indeterminate i.e not all the unknowns can be evaluated by statics alone.

Example 6.1: Determine the value of F and Ө so that particle A is in equilibrium.

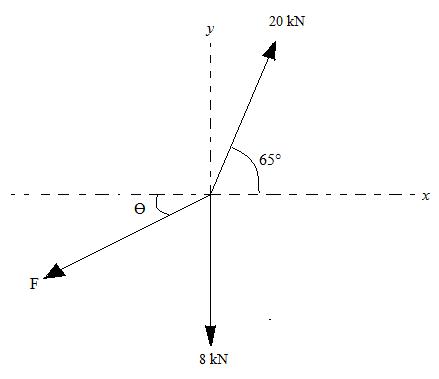
Fig. 6.1

 

Solution:

1. ∑ Fx = 20 cos 65° + F cos (180° + Ө) + 16 cos 270°

         = 4.23 – F cos Ө – 0

         = 0

Therefore, F cos Ө = 4.23

2. ∑ Fy = 20 sin 65° + F sin (180° + Ө) + 16 sin 270°

         = 18.13 – F sin Ө – 0

         = 0

Therefore,  F sin Ө = 18.13

3. tan Ө = \[{{F\sin \theta } \over {F\cos \theta }}\]  = \[{{18.13} \over {4.23}}\] = 4.29

Ө = 76.86°

F cos Ө = 4.23

F = \[{{4.23} \over {\cos 76.86^\circ }}\]  = 18.63 N