LESSON 12. FRICTION AND FRICTIONAL FORCES

12.1 INTRODUCTION

When two bodies in contact have a tendency to move over each other a resistance to the movement is set up. This resistance to the movement is called the Force of friction or simply friction. Friction depends upon the nature of the surface of contact. Friction acts parallel to the surface of contact. The direction of this frictional force on any one of the surfaces of contact will be opposite to the direction in which the contact surface tends to move. In other words, friction opposes motion.

  • Friction is an important force in many aspects of everyday life.
  • If there is too much friction, loss of energy, wear and tear of materials in contact occurs.
  • If there is less friction or no friction, this would result in ‘slipping’ all around.
  • For example oil in the engine of car is meant to minimize friction between moving parts in contact to reduce excessive friction for reducing loss of energy and material.
  • We need the friction between the tires on the road surface, to let the wheels roll. Friction is caused due to the unevenness of the surface of contact of bodies tending to move past each other.

When one body moves relative to the other, the tangential forces will always be developed along the surfaces of contact. These tangential forces are called frictional forces.

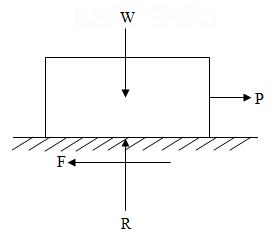
Module 4 Lesson 12 Fig.12.1

Fig.12.1

Fig.12.1 shows a wooden block resting on a rough horizontal table. Let W be the weight of the block. Let the block be subjected to a horizontal force P. When this applied force is sufficiently small, the block will remain in equilibrium. The rough table surface will exert a normal reaction R and a tangential reaction (friction) F on the block so as to keep the block in equilibrium. Resolving, the forces on the block vertically and horizontally, we get

R = W

and                                                                F = P

Suppose the force P is gradually increased. The friction F will also increase, so that at every stage of equilibrium F = P. But there is a limit to which friction can increase. We can not expect the frictional resistance to go on increasing infinitely as the force P is increased. Let F1 represent the greatest possible friction. Let P1 be the applied force corresponding to this condition. At this stage,

F1 = P1

If the applied force exceeds P1, the block will slip on the table since the friction resistance cannot increased beyond the value F1. The greatest possible friction depends upon the normal reaction. In the example given above the normal reaction is equal to W. When the block is at the point of sliding the ratio of this friction to the normal reaction is found to be a constant which depends upon the surfaces of contact. This contact is called the coefficient of friction.

i.e. If F is the frictional resistance when the block is in the limiting equilibrium

F = µR where µ is the coefficient of friction

 12.2 ANGLE OF FRICTION

Consider the block resting on the horizontal rough surface. Let Rꞌ be the resultant reaction      (resultant of the normal reaction R and friction F). The angle Ө between the resultant reaction and the normal to the surface is called the angle of friction.

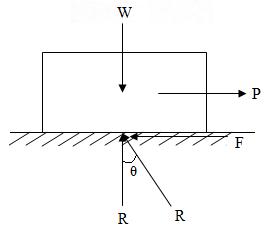
 Module 4 Lesson 12 Fig.12.2

Fig.12.2

Obviously, tanӨ =  \[{F \over R}\]

Corresponding to the limiting condition of equilibrium, the friction F will reach the maximum value. Corresponding this condition the angle of friction reaches a maximum value λ, so that

tan λ = \[{{{F_{max}}} \over R}\]   = µ

Therefore                                                           λ = \[{\tan ^{ - 1}}\mu\]

The inclination of the resultant reaction with the normal when the condition of limiting equilibrium is reached is called the angle of limiting friction.

Example: If coefficient of friction between all surfaces shown in Fig.12.3 is 0.30. What is the horizontal force required to get 250 kg block moving to the right?

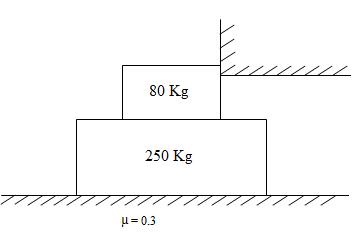
Module 4 Lesson 12 Fig.12.3

Fig.12.3

Solution: In this problem 80 kg block is completely restrained against motion and as we apply force P on 250 Kg block as shown in Fig.3, there is no force acting vertically at the contact surfaces between the obstacle and 80 kg block. Hence frictional force acts only at bottom and top surfaces of 250 kg block while only at lower surface of 80 kg block. Refer Fig.12.4.

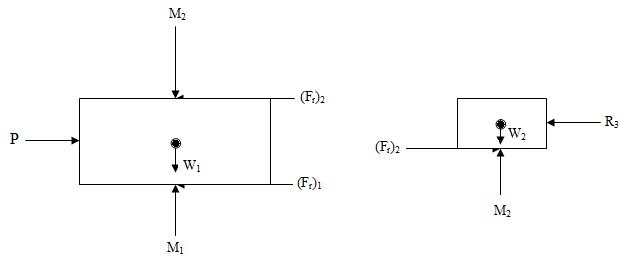
 Module 4 Lesson 12 Fig.12.4

(a)    Lower block                                                    (b) Upper block

Fig.12.4

Note that ∑ Fy = 0 for upper block gives M2 = W2

Therefore,                                            M2 = 80 × 9.81 = 784.8 N

For lower block,                                  ∑ Fy = 0 gives M1 = W1 + M2

Therefore,                                            R1 = (250 × 9.81) + 784.8 = 3237.3 N

Also                                                     (Fr)1 = µ R1 = (0.3) (3237.3) = 971.19 R

and                                                      (Fr)2 = µ R2 = (0.3) (784.8) = 235.44 R

∑ Fx = 0 for lower block gives P = (Fr)1 + (Fr)2

or                                                         P = 1206.63 N

Note - ∑ Fx = 0 is not necessary for upper block in this problem.

Example: A pull of 20 kN at 30° to the horizontal in necessary to move a block of wood on a horizontal table (Fig.12.5).If the coefficient of friction between the bodies in contact is 0.25, what is the weight of the block?

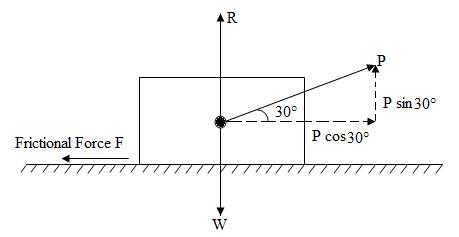
 Module 4 Lesson 12 Fig.12.5

Fig.12.5

Solution: Pull (P) = 20 kN, inclination of the force θ = 30° to the horizontal

Coefficient of friction, µ = 0.25

Let W = unknown weight of the block.

Resolving the forces horizontally, we get

F = P Cos30°

µR = P Cos30° ------------------------------------------------(i)

Resolving the forces perpendicular to the plane vertically, we get

R + P Sin30° = W

R = W – P Sin30° ------------------------------------------------------(ii)

Substituting the value of R in Eqn.(i), we get

µ(W – P Sin30°) = P Cos30°

0.25(W – 20 Sin30°) = 20 Cos30°

0.25(W – 10) = 17.32

W = 79.28 kN

Last modified: Tuesday, 10 September 2013, 6:29 AM