Site pages
Current course
Participants
General
MODULE 1. BASIC CONCEPTS
MODULE 2. SYSTEM OF FORCES
MODULE 3.
MODULE 4. FRICTION AND FRICTIONAL FORCES
MODULE 5.
MODULE 6.
MODULE 7.
MODULE 8.
LESSON 14. CONE OF FRICTION
14.1 CONE OF FRICTION
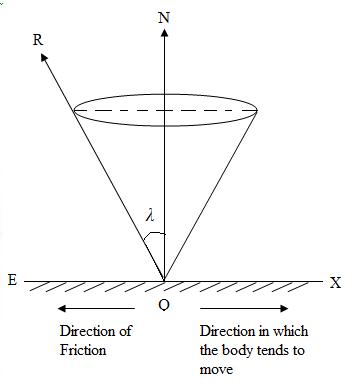
Fig.14.1
Let ON represent the normal reaction offered by a surface on a body (Fig.14.1). If OX is the direction in which the body tends to move then the force of friction acts in the opposite direction i.e, along OE. If the body be in limiting equilibrium the resultant R makes an angle λ with the normal ON.
Suppose the body is at the point of sliding in other direction, it is easily seen that the resultant reaction will make the same angle λ with the normal. Hence, when limiting friction is offered the line of action of the resultant reaction should always lie on the surface of an inverted right circular cone whose semi-vertex is λ. This cone is called the cone of friction.
Example: A block is weighing 50 kg is placed on a rough surface whose coefficient of friction is 0.30 and inclined force P is applied at its top corner as shown in Fig.14.2. Determine whether the block will tip or slide and the force P required to move the block.
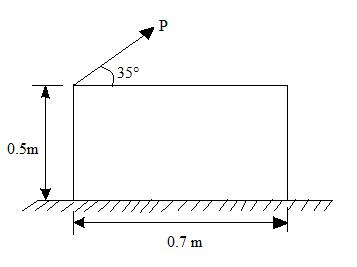
Fig.14.2
Solution: W = 50 × 9.81 = 490.5 N
By referring Fig.14.2
∑ Fy = 0
R1 – W + P sin 35°
R1 = 490.5 – 0.574 P
Or
Hence limiting friction force = µ R1
= 0.3 (490.5 – 0.574 P)
= 147.15 – 0.1722 P
Now F = P cos 35° using ∑ Fx = 0
So, F = 0.819 P
Let us assume that block slides before tipping,
Then 0.819 P = 147.15 – 0.1722 P
P = 148.46 N
Now check the tipping of block,
∑ M0 = 0 = (148.46 sin 35°) (0.35) + (148.46 cos 35°) (0.5) – N1 (x)
29.83 + 60.79 – R1 x = 0
90.62 = R1 x
By putting the value of R1, we get
90.62 = (490.5 – 0.574 P) x
x = 0.224 m
As x < 0.35 m, tipping will not occur.
Hence block slides with P = 148.46 N
Example: A ladder 5 m long weighing 200 N is resting against a wall at an angle 0f 60° to the horizontal ground. A man weighing 500 N climbs the ladder. At what position along the ladder from bottom does he induce slipping. The coefficient of friction for both the wall and the ground with the ladder is 0.2.

Fig.14.3
Solution: Let the ladder be at the point of sliding when the man is at a distance x metres from the foot of the ladder. See Fig.14.3.
Let F be the position of the man.
BF = x, BE = AE = 2.5m
Let the normal reactions at the floor and the wall be R and S. Friction at the floor and the wall will be 0.2R and 0.2S respectively.
Resolving the forces on the ladder horizontally and vertically,
S = 0.2R--------------(1)
R + 0.2S = 700 N-------------(2)
From equations (1) and (2), we get R = 673.08 N
S = 134.62 N
Taking moments about the lower end of the ladder,
200 × 2.5 cos 60° + 500 × x cos 60° = S × 5 sin 60° + 0.2S × 5 cos 60°
250 +250x = 2.5 S + 0.5 S
250 + 250x = S (2.5 + 0.5)
250 + 250x = 134.62 (2.5 + 0.5)
250 + 250x = 650.23
x = 1.60 m
Example: A block weighing 20 N is a rectangular prism resting on a rough inclined plane as shown in Fig.14.4.The block is tied up with a horizontal string which has a tension of 5 N. Find
(a) The frictional force on block
(b) Normal reaction of the inclined plane
(c) The coefficient of friction between the surfaces of contact
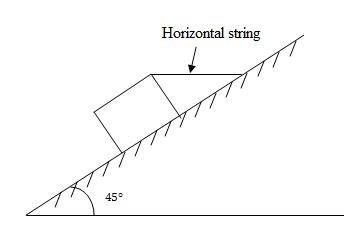
Fig.14.4
Solution: Weight of the block W = 20 N
Tension in the horizontal string T = 5 N
Angle of the inclined plane = 45°
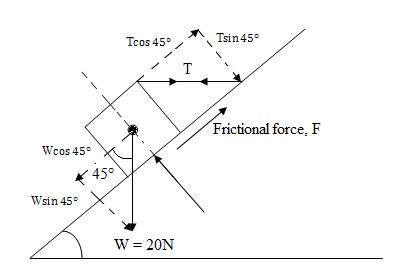
Fig.14.5
(dotted arrows indicate the components of the force along the tangential and normal to the inclined plane)
Resolving the force parallel to inclined plane, we get
F + T = W
By substituting the values, we get
F + 5 = 20
F = 10.6 N
(b) Resolving the force in the normal direction, we have
R = W + T
= 20 + 5
R = 17.68 N
By using the relation, F = µR
10.6 = µ × 17.68
µ = 0.59
Example: A body resting on a rough horizontal plane required to pull 20N inclined at 30° to the plane just to remove it. It was found that a push of 25N inclined at 30° to the plane just removed the body. Determine the weight of the body and the coefficient of friction.
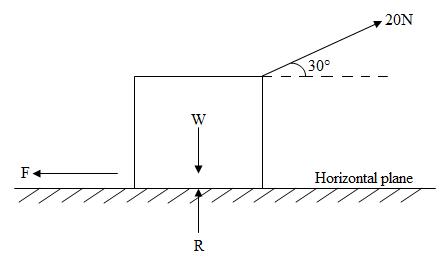
Fig.14.6
Solution: given, Pull = 20N, Push = 25N and θ = 30°
Let W = weight of the body in N, R = Normal reaction and µ = coefficient of friction
1. First of all,the pull acting on the body
Resolving the forces horizontally, we get
F = 20 = 20 × 0.866 = 17.32 N
Resolving the forces vertically, we get
R = W - 20 = W – 20 × 0.5 = (W – 10) N
According to the relation,
F = µ R
17.32 = µ (W – 10)…………………………………………………………………………..(i)
2. The push acting on the body
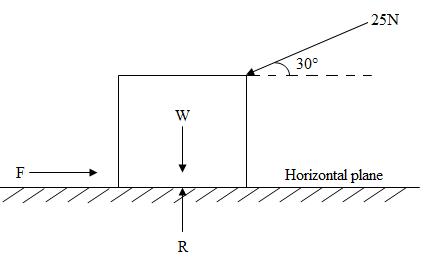
Fig.14.7
Resolving the forces horizontally, we get
F = 25 = 25 × 0.866 = 21.65 N
Now, resolving the forces vertically, we get
R = W + 25 = W + 25 × 0.5 = (W + 12.5) N
By using the relation,
F = µ R
21.65 = µ (W + 12.5)………………………………………………………………………...(ii)
Dividing the Eq. (i) to Eq. (ii), we get
\[{{17.32} \over {21.65}} = {{{\rm{\mu }}\left( {{\rm{W}} - 10} \right)} \over {{\rm{\mu }}\left( {{\rm{W}} + 12.5} \right)}}\] = \[{{W - 10} \over {W + 12.5}}\]
By simplification, we get
W = 100 N
Now, substituting the value of W in both Eq. (i) and Eq. (ii), we get
µ = 0.192