Engineering Mechanics 3(2+1)

LESSON 13. ANGLE OF REPOSE

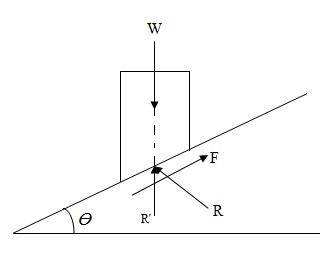
Fig.13.1 shows a block of weight W resting on a rough inclined plane inclined at Ө with the horizontal plane. Let R be the normal reaction and F be the friction. Resolving the forces along the plane, W sinӨ = F ..............................................(i)

Resolving the forces normal to the plane, W cosӨ = R .....................................(ii)

From equation (i) and (ii), tanӨ = \[{F \over R}\]

But we know that the tangent of the angle of friction is also equal to \[{F \over R}\] .

Therefore, Angle of the plane = Angle of friction

Suppose the angle of the plane, Ө is increased to a value ϕ so that the block is at the point of sliding. Corresponding to this condition,

tanϕ = \[{{{F_{max}}} \over R}\] = µ = \[{\tan ^{ - 1}}\lambda\]

Therefore, ϕ = λ

The maximum inclination of the plane at which a body can remain in equilibrium over the plane entirely by the assistance of friction is called the angle of repose.

Obviously angle of repose ϕ = Angle of limiting friction λ.

Example: If the weight of the body is 130 N is at rest on a horizontal plane. A horizontal force of 100 N will just cause it to slide, Determine the limiting friction and coefficient of friction.

Solution: F_max = limiting friction

                          = Greatest force applied horizontally on the body resting on the horizontal

Plane = 100 N

Coefficient of friction = µ = \[{{{F_{max}}} \over R}\]  = \[{100 \over 130}\] = 0.77

Example: The coefficient of friction between a body of weight 120 N and a horizontal plane on which it rests is 0.6. (a) Calculate the horizontal force which acting on the body can just cause it to slide, (b) What least horizontal force would cause the body to slide if an additional weight of 30 N be added to the body?

Solution:  (a) Normal Reaction R = 120 N

Coefficient of friction = µ = 0.6

Therefore, Maximum friction possible = µR = 0.6 × 120 = 72 N

Therefore, Horizontal force required to just make the body slide = 72 N

(a) Normal Reaction = 120 + 30 = 150 N

(b) Maximum friction = µR = 0.6 × 150 = 90 N

Therefore, least force necessary to cause sliding = 90 N

13.2 LAWS OF FRICTION

The following are the laws of friction:

(i) Friction in non-limiting equilibrium

(ii) Friction in limiting equilibrium

(iii) Friction during motion

First Law (Applicable to non-limiting, limiting and dynamic condition). Friction always opposes motion. Frictional forces come into play only when a body is urged to move. Frictional force will always act in a direction opposite to that in which the body is urged to move.

Second Law (Applicable to non-limiting condition of equilibrium). The magnitude of the frictional force is just sufficient to prevent the body from moving. That is, only as much resistance as required to prevent motion will be offered as friction.

Third Law (Applicable to limiting condition of equilibrium). The limiting frictional resistance bears a constant ratio with the normal reaction. This ratio depends on the nature of the surfaces of contact. The limiting frictional resistance is independent of the area of contact.

Fourth Law (Friction during motion i.e Kinetic Friction). When motion takes place as one body slides over the other the magnitude of the frictional resistance will be less than that offered at the condition of limiting equilibrium. The magnitude of the friction will depend only on the nature of the sliding and independent of the shape or the extent of the contact area.

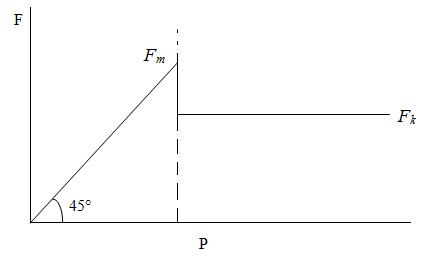
Fig.13.2

When a body resting on a horizontal surface is subjected to gradually increasing horizontal force P the condition F = P is satisfied as long as the body is in equilibrium. In the condition of equilibrium, the maximum value of the friction is F_m which occurs when the body is in limiting equilibrium. If the horizontal force P on the body is further increased, then the equilibrium of the body is broken and the body moves over the surface. In this condition the value of the friction is F_k which is less than F_m.

Example: A 150 N block is placed on a rough horizontal surface as shown in Fig.13.3 knowing that block just slides for P = 50 N and Ө = 20°, determine µ. For same Ө =20° and same µ, determine magnitude of P to just slide the same block, ‘P’ being applied in .opposite direction, at same point O.

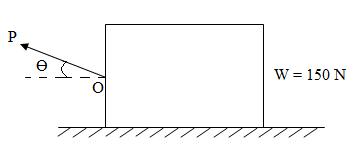
Fig.13.3

Solution: Refer Fig.13.3 showing Free Body Diagram of the block for case I

 

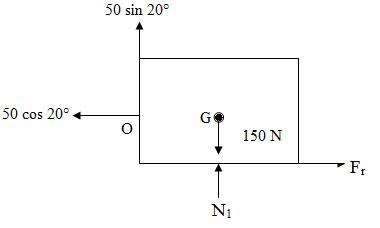
Fig.13.3(Case I)

∑ F_x = 0 gives F_r = 50 cos 20°  

Where F_r = µ R₁                              

R₁ = 150 – 50 sin 20° = 132.9 N

µ (132.9) = 50 cos 20°

µ = 0.353

Fig.3(Case II) shows Free Body Diagram of same block for ‘P’ in opposite direction.

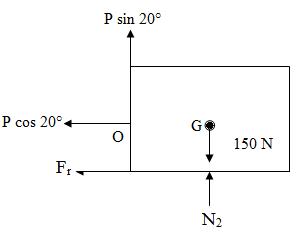
Fig.13.3(Case II)

 

Here R₂ = 150 + P sin 20°    And F_r = P cos 20° = R₂

P (0.939) = 0.353 (150 + 0.342P)

P = 64.73 N

Example: Two bodies weighing 120 kN and 100 kN rest on an inclined plane and are connected by a chord which is parallel to the plane. The body weighing 100 kN is below the one weighing 120 kN and coefficient of friction for 100 kN body is 0.2 and that for 120 kN is 0.3. Find the inclination of the plane to the horizontal and the tension in the chord when motion is about to take place, down the incline.

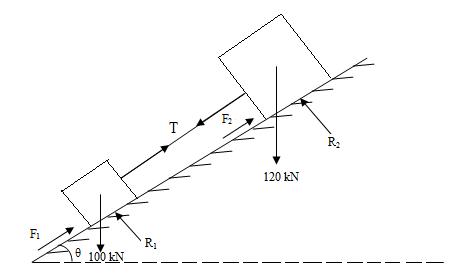
Fig.13.4

Solution: Consider the weight of body A, i.e. 100 kN.

Resolving the forces parallel and perpendicular to the inclined plane, we get

F₁ + T – 100 Sinθ = 0

µR₁ + T – 100 Sinθ = 0

0.20R₁ + T – 100 Sinθ = 0

T = 100 Sinθ – 0.25R₁

R₁ = 100 Cosθ

100 Sinθ – T = 0.20 × 100 Cosθ -----------------------------------------------------(i)

Consider the body B, i.e. 120 kN.

Resolving the forces parallel and perpendicular to the inclined plane, we get

F₂ – T – 120 Sinθ = 0

0.3R₂ – T = 120 Sinθ

R₂ = 120 Cosθ

0.3 × 120 Cosθ – T = 120 Sinθ--------------------------------------------------------(ii)

Solving Eqn. (i) and (ii), we get

100 Sinθ – T = 25 Cosθ

36 Cosθ – T = 120 Sinθ

100 Sinθ – 25 Cosθ = 36 Cosθ – 120 Sinθ

61 Cosθ = 220 Sinθ

tanθ = \[{{61} \over {220}} = 0.277\]

θ = 15.49°

Therefore, T = 2.62 kN