Engineering Mechanics 3(2+1)

LESSON 16.

16.2 METHOD OF JOINTS

After determining the reaction at the supports, the equilibrium of each joint is considered one by one.

• Each joint will be in equilibrium if ∑ V= 0 and ∑ H = 0, these two conditions are satisfied.

• Forces in the members will either be tensile in nature or compressive in nature.

• The joint is selected in such a way that at any time there are not more than two unknowns.

The direction of an unknown force is assumed.

• If the magnitude of force comes out to be positive than assumed direction will be correct.

• If the magnitude of force comes out to be negative than assumed direction will be incorrect.

The process is continued until all the joints are considered thereby calculating the forces in all the members of the frame.

Example: Find the forces in the members AB, BC, AC of the truss shown below in Fig.16.1. End A is hinged and B is supported on rollers.

Fig.16.1

Solution: A roller offers a reaction perpendicular to plane of rolling. Let R_B is reaction at B. A hinge offers two reaction components one in vertical direction and another in horizontal direction. Since the load of 5O kN acts vertically downward, therefore only vertical direction R_A is developed and no horizontal reaction.

From the geometry of the figure, the distance of 50 kN load from A in horizontal direction along AB is AC cos60°.

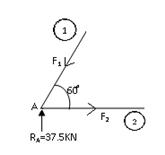
Fig.16.2                                       Fig.16.3

In ΔACB,

Angle  at ACB = 90°

AC = AB cos 60° = 6 × \[{1 \over 2}\] = 3 m

BC = AB sin 60° = 6 × \[{{\sqrt 3 } \over 2}\]  = 3 \[\sqrt 3\] m

Distance of 50 kN load from A = AC cos 60° = 3 ×  = 1.5 m

Taking moments about A, we have

R_B × 6 = 50 × 1.5

R_B = \[{{50 \times 1.5} \over 6}\] = 12.5 kN

For equilibrium ∑ V = 0, i.e.

R_A + R_B = 50

R_A + 12.5 = 50

R_A = 37.5 kN

Considering equilibrium of joint A, first because R_A is known and only two unknown forces F₁ and F₂ are there. At each joint two equation of statical equilibrium are available i.e.

∑ V = 0 and ∑ H = 0.

Let F₁ is force produce in the member AC and F₂ is the force produced in the member AB as shown in Fig.2. Joint A has to be in equilibrium. Component of force F₁ in vertical direction will balance vertical reaction R_A. Therefore, the arrow is marked in member (1) in down direction. Applying condition ∑ V = 0 at joint A.

F₁ sin 60° = 37.5

F₁ = 37.5 × \[{2 \over {\sqrt 3 }}\]  = \[{75 \over {\sqrt 3 }}\]  = \[{75 \over {\sqrt 3 }}\]   ×  \[{{\sqrt 3 } \over {\sqrt 3 }}\]

= + 25 \[\sqrt 3\] kN (+ve sign indicates that as assumed direction is correct)

= 43.30 kN

As the force F₁ is pushing joint A, therefore F₁ is compressive force. Mark arrow at joint C as pushing it to show that member AC is compression member (Fig.16.2)

Now applying condition ∑ H = 0 at joint A,

F₁ cos 60° = F₂

Therefore, F₂ = 43.30 × \[{1 \over 2}\]  = + 21.65 kN

(again +ve sign indicated that the arrow marked in member AB is correct)

As the force F₂ is pulling the joint A, therefore F₂ is a tensile force. At B, place arrow marking away from B to show that member AB is a tension member.

Next consider joint B, as shown in Fig.16.3

Let F₃ is the force produced in the member BC. The joint B has to be in equilibrium. It must satisfy the two conditions of statical equilibrium viz. ∑ V = 0 and ∑ H = 0. Let us assume the direction of arrow towards B.

Applying ∑ V = 0 at joint B.

F₃ sin 30° = 12.5

Therefore F₃ = + 25 kN (+ve sign indicates that direction of F₃ is correct)

As F₃ pushes the joint B, Therefore it is a compressive force.

Now applying second condition ∑ H = 0 at the joint B,

F₃ cos 30° = F₂

25 × \[{{\sqrt 3 } \over 2}\] = 21.65

21.65 = 21.65        (Check)

Now the forces in the various members are tabulated in the following table.

Member	Force
AB	Tensile = 21.65 Kn
BC	Compressive = 25 kN
AC	Compressive = 43.30 kN

 Forces are marked in the truss, as shown in Fig.16.4. If we take tensile forces as +ve, then compressive force will be –ve.

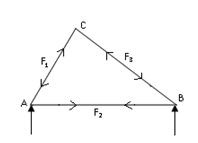
Fig.16.4

Example: Determine the forces in the members of the truss loaded as shown in the Fig.16.5. Also indicate the nature of the force (tensile or compressive).

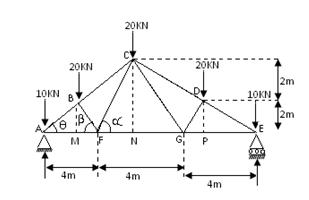
Fig.16.5

Solution: The truss is symmetrical and also loaded symmetrically therefore, reactions R_A and R_B will be equal. From the condition of equilibrium

∑ V = 0

i.e. R_A + R_B = 10 + 20 + 20 + 20 +10

2R_A = 80

R_A = 40 kN, R_B = 40 kN   

 Draw BM and CN perpendicular to AE.

In Δ CAN, tan CAN =  = 33.69°

Q = angle at CAN = 33.69°

ΔCFN, tan α =  = 2

α = 63.43°

AC = \[\sqrt {A{N^2} + C{N^2}}\] = \[\sqrt {{6^2} + {4^2}}\]  = 7.2 m

AB = 3.6 m, BM = 3.6 sin 33.69° = 1.99 m

AM = AB cos Ө = 3.6 cos 33.69° = 2.99 m

MF = AF – AM = 4 – 2.99 = 1.01 m

tan β = \[{{BM} \over {MF}}\]  = \[{2 \over {1.01}}\]  = 1.98

β = 63.20° = α

Considering joint A, (Fig.16.6). At this joint four forces are acting, out of which two forces AB and AF are unknown. Applying condition of equilibrium at joint A, ∑ V = 0. Resolving all forces in a vertical direction, we have

Fig.16.6

10 + AB sin Ө = 40 ..........................(i)

∑ H = 0

Resolving all forces horizontally, we have

AB cos Ө = AF................................(ii)

(Here AF is assumed to be in tension and AB is assumed to be in compression)

From (i), AB × sin 33.69° = 30

Therefore, AB = \[{{30} \over {\sin 33.69^\circ }}\]  = \[{{30} \over {0.5547}}\]

= + 54.08 kN (compression)

From (ii), AF = 54.08 cos 33.69°

= 44.99 kN (tensile)

Considering joint B, (Fig.16.7)

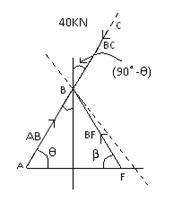
Fig.16.7

 

Angle ABF = 180° - Ө – β

                    = 180° - 33.69° - 63.20°

                    = 83.11°

Resolving all forces perpendicular to ABC,

BF sin 83.11° = 20 sin (90 – Ө)

BF × 0.9928 = 20 cos Ө = 20 × 0.8320

BF = 16.76 kN (compressive)

Resolving all forces along the line ABC,

AB + BF cos 83.11° = BC + 20 cos (90 – Ө)

54.08 + (16.76 × 0.1199) = BC + (20 × 0.5547)

56.089 = BC + 11.094

BC = 44.49 KN (compressive)

Considering joint F, (Fig.16.8)

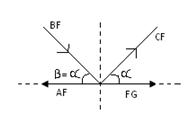
Fig.16.8

Resolving all forces vertically

BF sin α = CF sin α

Therefore, CF = 16.76 kN (tensile)

Resolving all forces in horizontal direction.

FG + CF cos α + BF cos α – AF = 0

Therefore, FG + 16.76 cos 63.20° + 16.76 cos 63.20° - 44.99 = 0

Therefore, FG + 7.56 + 7.56 – 44.99 = 0

FG + 15.12 – 44.99 = 0

FG = 29.87 KN (tensile)

We have analysed half the truss, other half is symmetrical, therefore

AF = EG, AB = ED, BC = DC, BF = DG, CF = CG

Member	Force	Nature
AB	54.08 KN	Compressive
BC	44.99 KN	Compressive
CD	44.99 KN	Compressive
DE	54.08 KN	Compressive
AF	44.99 KN	tensile
FG	29.87 KN	tensile
GE	44.99 KN	tensile
FB	16.76 KN	Compressive
FC	16.76 KN	tensile
GD	16.76 KN	Compressive
GC	16.76 KN	tensile