Farm Power & Machinery Management 3(2+1)

Lesson 10. Cost of Operation of Farm Equipment

Fixed Costs: These costs depend on how long a machine is owned rather than how much it is used. Fixed costs include the following:

1) Depreciation

2) Interest

3) Taxes

4) Shelter

5) Insurance

Operating Costs: It is also called as the variable costs. It varies in proportion to the amount of machine used. The operating costs consist of the following:

1) Repair and maintenance costs

2) Fuel costs

3) Oil or lubrication costs

4) Labour costs

Fixed Costs

Depreciation: Depreciation means a loss in the value of a machine due to time and use. Often, it is the largest of all costs. Machine depreciate, or have a loss of value, for several reasons, such as, age of machine, wear and tear of machine and obsolescence. There are several different methods to calculate the depreciation. These include the following:

1) Estimated value method

2) Straight-line method

3) Declining-balance method

4) Sum-of-the years digits method

5) Sinking-fund method

Estimated Value Method: It is the most realistic determination of depreciation. At the end of each year the value is compared with the value of machine possessed at the start of the year. The difference is the amount of depreciation. Table 3.2 gives the estimated values as the percentage of the purchase price for most of the expensive farm machineries.

Table 3.2:  Estimated values of depreciation at the end of year.

Machine	% of purchase price
	1	2	3	4	5	6	7	8	9	10
Tractor	36	6	5	5	5	4	4	3	3	3
Self-propelled combine	41	7	6	6	5	5	4	4	3	3
Tractor-drawn combine	46	7	6	5	5	4	4	3	3	2
Corn picker	49	6	5	5	4	4	3	3	2	2
Baler	49	6	5	5	4	4	3	3	2	2
Forage harvester	53	6	5	4	4	4	3	3	3	3
Cotton picker	43	6	6	5	4	4	4	3	3	1

Straight-line Method: In the straight-line depreciation method, an equal reduction of value is used for each year the machine is owned (Fig. 1). This method can always be used to estimate costs on a specific period of time, provided the proper salvage value is used for the age of the machine. The annual depreciation value can be calculated from the following expression

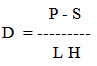
Where,

D         = average annual depreciation, Rs/h

P          = purchase price, Rs.

S          = salvage value, taken as 10% the purchase price

L          = life of machine, years

H         = annual use of machine, hours

The straight-line depreciation method is not quite accurate for giving the value of a machine at same age. In actual practice machine depreciates much faster in the first few years than in the later years.

Fig. 1: Straight line depreciation.

 

Example: Suppose a new tractor is purchased for Rs. 3,00,000.00 and its life is assumed to be 15 years. Assume salvage value as 10% of purchase price; then average annual depreciation would be

 

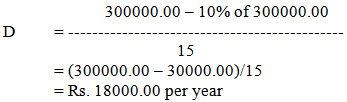
Declining-balance depreciation method: It reflects the actual value of a machine at any age rather than the value found from the straight-line method or sum of the digits method. With the declining balance method, a machine depreciates a different amount for each year, but the annual percentage of depreciation is the same (Fig. 2). Depreciation can be calculated by using the following expression

D_n+1       = V_n - V_n+1

V_n          = P (1- X/L)ⁿ

V_n+1       = P (1 - X/L)ⁿ⁺¹

D_n+1       = P(1 - X/L)ⁿ (X/L)

Where.

D_n+1       = amount of depreciation charged for year n+1, Rs./year

V         = remaining value at any time

P          = purchase price, Rs.

n          = number representing age of machine in years at the beginning of year in question

L          = life of machine, years

           X          = ratio of depreciation rate.  It may be any number between 1 and 2. If X = 2 the method is called double-declining-balance method.

                         For used machine X  is taken as 1.5.

Example: Suppose a new tractor is purchased for Rs. 3,00,000.00 and its life is assumed to be 15 years. Assume salvage value as 10% of purchase price; then find the depreciation in 6^th year.

D_n+1       = V_n - V_n+1

V_n          = P (1- X/L)ⁿ

V_n+1       = P (1 - X/L)ⁿ⁺

Given              n = 5; X = 2 for new machine and L = 15

V_n          = 300000 (1- 2/15)⁵                     

                        = 146683.65

V_n+1       = 300000 (1- 2/15)⁶                     

                         = 127125.83

D_n+1       = V_n - V_n+1

                         = 146683.65 – 127125.83 = 19557.82 in 6^th year

Example: A machine costing Rs. 3,00,000.00 has a total life of 15 years. If the rate of inflation is taken as 5% constant through out its life period, find the future price of machine, total depreciation, remaining value and annual depreciation charge at the end of 12^th year. Take salvage value as 10% of inflated price.

Solution:

Using equation (1) future price at the end of 12^th year will be

F          = P (1 + I)ⁿ

                              = 300000 (1 + 0.1)¹²

                        = 941528.51

Total depreciation after elapse of 12 years will be

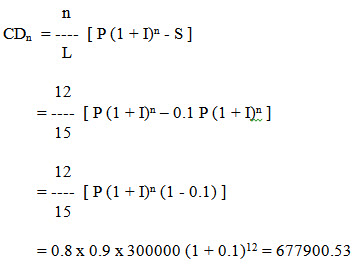
Remaining value of the machine at the end of 12^th year will be

= 941528.51 - 677900.53        = 263627.98

Annual depreciation charge in the 12^th year using equation (6) will be

= 0.06 P  [n (1 + I)ⁿ  -   (n-1)  ( 1 + I)^n-1   ]

= 0.06 x 300000  [12 (1 + 0.1)¹²  -   (12-1)  ( 1 + 0.1)^12-1   ]

= 0.06 x 300000 [37.66 – 31.38]

= 113040.00

Thus, it can be seen that at the higher inflation rates the financial burden on the farming enterprise will be very high. The above technique can be applied to other depreciation methods with constant/variable inflation rated in the life span of a farm machines.