Site pages
Current course
Participants
General
Module 1. Role of mechanization and its relationsh...
Module 2. Performance and power analysis
Module 3. Cost analysis of machinery- fixed cost a...
Module 4. Selection of optimum machinery and repla...
Module 5. Break-even point and its analysis, relia...
Module 6. Mechanization planning
Module 7. Case studies and agricultural mechanizat...
Topic 8
Topic 9
Topic 10
Lesson 11. Cost of Operation of Farm Equipment - continued
Sum-of-the Years Digits Method
It is a much more accurate method of estimating the true value of a machine at any age because the annual depreciation rate decreases as the machine gets older (Fig. 3). The amount of depreciation can be determine by
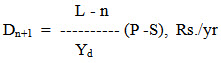
Where,
Yd = Sum of the years digits = L(L + 1)/2
n = age of the machine in years at the beginning of the year in question
L = life of machine, year
P = purchase price, Rs.
S = salvage value, Rs.
The following steps determine the amount of depreciation by the sum-of-the years digits method:
1) Add up the numbers representing the years covered by the depreciation method.
2) Divide the total depreciation by sum of the digits of the years for the depreciation period.
3) Proportion the depreciation in reverse of the years over which the depreciation occurs.
Example: Suppose a new tractor is purchased for Rs. 3,00,000.00 and its life is 15 years. Assume salvage value as 10% of the purchase price. Find the depreciation.
Solution:
Step 1: The sum-of-the-digits for 15 years is
15+14+13+12+11+10+9+8+7+6+5+4+3+2+1 = 120
Step II: Total depreciation = 300000.00 – 10% x 300000.00 = 270000.00
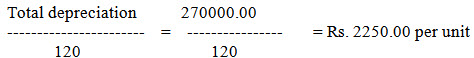
Step III: Each year depreciation would be calculated as follows:
First years’ depreciation = (L – n) x 2250.00
For first year n = 0
First years’ depreciation = (15 – 0) x 2250.00 = 33750.00
Second years’ depreciation = (15 – 1) x 2250.00 = 31500.00
Third years’ depreciation = (15 – 2) x 2250.00 = 29250.00
Fourth years’ depreciation = (15 – 3) x 2250.00 = 27000.00
And so on
Comparison of depreciation cost by different methods taking life of machine 15 years, price of machine P and salvage value 10% of P is given in Table 1.
Table 1: Comparison of depreciation cost by different methods.
(Life of machine = 15 years; Price of machine = P; Salvage value = 10% of P)
|
End of year |
Straight-line method |
Declining-balance method |
Sum-of-the-years digits method |
|
1 |
0.06 P |
0.1153 P |
0.1125 P |
|
2 |
0.06 P |
0.1000 P |
0.1050 P |
|
3 |
0.06 P |
0.0867 P |
0.0975 P |
|
4 |
0.06 P |
0.0751 P |
0.0900 P |
|
5 |
0.06 P |
0.0651 P |
0.0825 P |
|
6 |
0.06 P |
0.0565 P |
0.0750 P |
|
7 |
0.06 P |
0.0490 P |
0.0675 P |
|
8 |
0.06 P |
0.0425 P |
0.0600 P |
|
9 |
0.06 P |
0.0368 P |
0.0525 P |
|
10 |
0.06 P |
0.0319 P |
0.0450 P |
|
11 |
0.06 P |
0.0277 P |
0.0375 P |
|
12 |
0.06 P |
0.0240 P |
0.0300 P |
|
13 |
0.06 P |
0.0208 P |
0.0225 P |
|
14 |
0.06 P |
0.0180 P |
0.0150 P |
|
15 |
0.06 P |
0.0156 P |
0.0075 P |
Sinking-Fund Method
Sinking fund depreciation method is primarily advantageous for use with a planned replacement internal policy. By formula the values for the sinking fund annual payment (SFP) and the value at the end of the year n are:
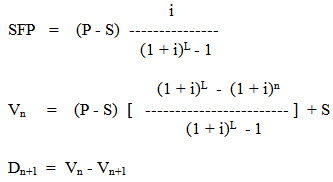
Where,
Dn+1 = amount of depreciation charged for year n+1, Rs./year
Vn = remaining value at the end of the year n, Rs.
Vn+1 = remaining value at the end of the year n+1, Rs.
P = purchase price, Rs.
S = salvage value, Rs.
i = interest rate, fraction
L = life of machine, years