Ground Water, Wells and Pumps

Lesson 26 Power Requirement and Efficiency of Centrifugal Pumps

26.1.1 Water Power

Water power is the theoretical power required for pumping. It is the power required by a pump in lifting a given quantity of water in a unit time assuming no losses of power in the pump. The water power (WP) of a pump can be calculated using the following equation:

 

                                        (26.1)

 

Where, WP = water power (W), = specific weight of the water (N/m³), Q = discharge of the pump (m³/s), and H = total head or total dynamic head (m).

 

26.1.2 Shaft Power

Shaft power is the power required at the pump shaft. It takes into account the loss of power in the pump. Shaft power (SP) of a pump can be computed using the following equation:

  

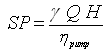                                            (26.2)

Where, is the overall efficiency of the pump (in fraction) and the remaining symbols have the same meaning as defined earlier. If the SI units of γ, Q and H are used, the unit of SP will be in watts (W).

 

26.1.3 Brake Power

It is the actual power to be supplied by the prime mover (engine or electric motor) for driving a pump. When there is direct drive from an engine or electric motor to the pump, the brake power is equal to the shaft power. In this case, the drive efficiency is assumed to be 100%. However, if belt or other indirect drives are used to run a pump, the brake power (BP) needs to be computed. Brake power (BP) can be calculated as:

 

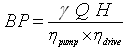                                       (26.3)

 

Where, is the efficiency of the drive (in fraction) and the remaining symbols have the same meaning as defined earlier. Like the WP and SP, if the SI units of, Q and H are used, the unit of BP will be in watts (W).

 

26.1.4 Input Power

Input power (IP) of a pump is defined as the ratio of brake power to the efficiency of the motor or engine used for driving the pump. Mathematically, it is expressed as:

 

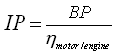                                         (26.4)

 

Where,  is the efficiency of the motor or engine (in fraction). If the SI unit of BP is used for calculating IP, the unit of IP will be in watts (W).

 

As mentioned above, if the SI units are used to compute WP, SP, BP and IP, the units of power will be in watts (W), which can be converted into horsepower (a popular unit of power) by dividing the power in watts with 746.

 

26.1.5 Energy Consumption by a Pump

The energy consumption by a pump can be calculated as follows:

 

Energy Consumption = Input Power × Hours of Pump Operation          (26.5)

 

26.1.6 Illustrative Example

Problem (Michael et al., 2008): A pump lifts 100,000 liters of water per hour against a total head of 20 m. Calculate water power of the pump. If the pump has an efficiency of 75%, what size of prime mover is required to operate the pump? If a direct drive electric motor with an efficiency of 80% is used to operate the pump, compute the cost of electric energy in a month of 30 days. Assume that the pump is operated for 12 hours per day for 30 days and that the cost of electricity is Rs 5.00 per Unit.

 

Solution: From the question, we have:  Discharge of the pump (Q) = 100,000 L = 0.028 m³/s, Total head (H) = 20 m, Efficiency of the pump () = 75%, Efficiency of the motor = 80%, and Cost of electricity = Rs 5.00/Unit.

 

Water Power,  WP = γ×Q×H = 9810 × 0.028 × 20 = 5493.6 W, Ans.

 

Shaft Power, 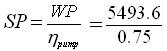   = 7324.8 W, Ans.

 

Note that since direct drive is used to operate the pump, the shaft power determines the required size of the prime mover.

 

Now, Input Power,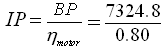   = 9156 W

 

Total energy consumption per month = Input Power × Hours of Pump Operation

                                                          = 9156 × 12 × 30

                                                        = 3296160 watt-hours (Wh)

                                                        = 3296.16 Kilowatt-hours (kWh)

 

As we know that 1 kWh is equal to 1 Unit, therefore, the cost of electric energy = Rs. (3296.16 × 5) = Rs. 16480.80, Ans.

 

26.2 Efficiency of Centrifugal Pumps

The efficiency  of a centrifugal pump can be expressed in four ways (Modi and Seth, 1998) and accordingly it is classified as: (i) Manometric efficiency, (ii) Volumetric efficiency, (iii) Mechanical efficiency, and (iv) Overall efficiency.

 

26.2.1 Manometric Efficiency

Manometric efficiency (h_mano) is defined as the ratio of the manometric head developed by the pump to the head imparted by the impeller to the liquid. That is,

 

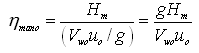                                   (26.6)

 

Where, V_wo = velocity of whirl of the liquid at the exit point (outlet) of the impeller; and u_o = peripheral (or, tangential) velocity of the impeller at the vane outlet.

 

If Q = discharge of the pump (i.e., volume of liquid actually delivered per second by the pump), and = specific weight of the liquid, then the manometric efficiency (h_mano) can also be expressed as follows:

 

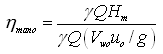                                          (26.7)

 

26.2.2 Volumetric Efficiency

Volumetric efficiency (h_vol) is defined as the ratio of the quantity of liquid discharged per second from the pump to the quantity of liquid passing per second through the impeller. Leakage loss occurs in the centrifugal pump and if this loss is represented by, then the volumetric efficiency is given as:

 

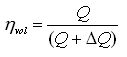                                        (26.8)

 

Where, Q is the actual discharge of the pump.

 

26.2.3 Mechanical Efficiency

Mechanical efficiency (η_mech) is defined as the ratio of the power actually imparted by the impeller to the power supplied to the shaft by the prime mover. That is,

 

                            (26.9)

 

Eqn. (26.9) means h_mech = Actual Power imparted by the impeller ¸ Shaft Power, which can be mathematically expressed as:

 

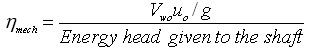                    (26.10)

 

Or, 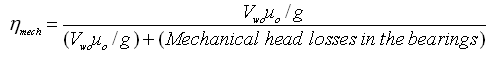               (26.11)      

 

26.2.4 Overall Efficiency

Overall efficiency (η_o) of a pump is defined as the ratio of the power output from the pump to the power input to the pump from the prime mover. That is,

 

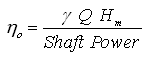                                 (26.12)

 

Note that the overall efficiency (h_o) can also be calculated as the product of η_mano, _ηvol and η_mech. That is,

 

                        (26.13)

 

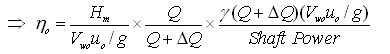                 (26.14)

 

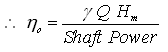                                       (26.15)

 

Equation (26.15) is the same as the expression obtained from the definition of overall efficiency [i.e., Eqn. (26.12)].

 

References

Michael, A.M., Khepar, S.D. and Sondhi, S.K. (2008). Water Well and Pump Engineering. Second Edition, Tata McGraw Hill Education Pvt. Ltd., New Delhi.

Modi, P.N. and Seth S.M. (1998). Hydraulics and Fluid Mechanics. Twelfth Edition, Standard Book House, New Delhi.

 

Suggested Readings

Michael, A.M., Khepar, S.D. and Sondhi, S.K. (2008). Water Well and Pump Engineering. Second Edition, Tata McGraw Hill Education Pvt. Ltd., New Delhi.

Murty, V.V.N. and Jha, M.K. (2011). Land and Water Management Engineering. Sixth Edition, Kalyani Publishers, Ludhiana.

Schwab, G.O., Fangmeier, D.D., Elliot, W.J. and Frevert, R.K. (2005). Soil and Water Conservation Engineering. Fourth Edition, John Wiley and Sons (Asia) Pte. Ltd., Singapore.

QUIZ

State whether the following statements are true (T) or false (F):

1. ‘Input power’ is the theoretical power required for pumping.
2. ‘Water power’ is the power required by a pump in lifting a given quantity of water in a unit time assuming no losses of power.
3. For the pumps directly driven by the electric motor, the ‘brake power’ is equal to the ‘shaft power’.
4. Power imparted by the impeller is equal to the power delivered by the motor to the shaft.
5. ‘Mechanical efficiency’ of a centrifugal pump is the ratio of the actual power imparted by the impeller to the ‘shaft power’.