Strength of Material

LESSON 5. Deflection of Beam: Moment-Area Method

\[{d \over {dx}}\left( {{{dy} \over {dx}}} \right)=-{M \over {EI}}\]                                                                                       (5.1)

\[\Rightarrow {\left( {{{dy} \over {dx}}} \right)_A}- {\left( {{{dy} \over {dx}}} \right)_B}=\int\limits_{{x_A}}^{{x_B}} {{{Mdx} \over {EI}}}\]                                                 (5.2)

where, \[{\left( {{{dy}/ {dx}}})_A}-{\left( {{{dy} / {dx}}} \right)_B}\]   , hereafter referred to as \[{\theta _{AB}}\]  is the angle between tangents at A and B as illustrated in Figure 5.1a. Similarly the deflection at B with respect to tangent at A, may be written as,

\[{\delta _{AB}}=\int\limits_{{x_A}}^{xB} {xd\theta }=\int\limits_{{x_A}}^{{x_B}} {{{Mxdx} \over {EI}}}\]                                                                                    (5.3)

It is to be noted that \[\int\limits_{{x_A}}^{{x_B}} {{{Mxdx}/{EI}}}\]  represents the statical moment with respect to B of the total bending moment area between A and B, divided by EI. Therefore equation (5.3) may also be written as,

\[{\delta _{AB}}=\left[ {\int\limits_{{x_A}}^{{x_B}} {{{Mdx} \over {EI}}} } \right]\bar x\] ,                                                                                          (5.4)

\[\Rightarrow {\delta _{AB}}=\bar x{\theta _{AB}}\] ,                                                                                              (5.4)

where \[\bar x\] is the centroidal distance as shown in Figure 5.1a.

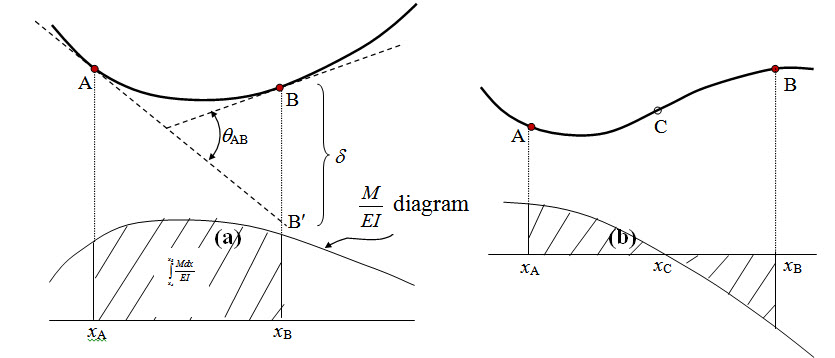Fig. 5.1.

Based on equations (5.2) and (5.4) the moment-area theorem may be stated as,

Theorem 1

The change in slope between the tangents drawn to the elastic curve at any two points A and B is equal to the area of bending moment diagram between A and B, divided by EI.

Theorem 2

The deviation of any point B relative to the tangent drawn to the elastic curve at any other point A, in a direction perpendicular to the original position of the beam, is equal to the moment with respect to B of the area of bending moment diagram between A and B, divided by EI

Applications of the Moment-area theorem will now be demonstrated via several examples.

5.2 Example 1

A simply supported beam AB is subjected to a uniformly distributed load of intensity of q as shown in Figure 5.2. Calculate the deflection at the midspan. Flexural rigidity of the beam is EI.

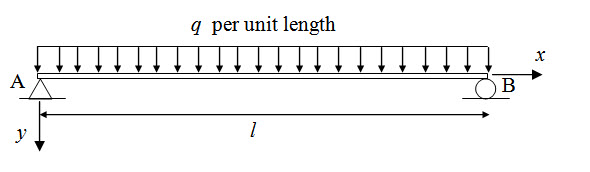Fig. 5.2.

Solution

From Example 4.1, bending moment at a distance x from A is,

\[{M_x}={{ql} \over 2}x - {{q{x^2}} \over 2}\]                                      (4.4)

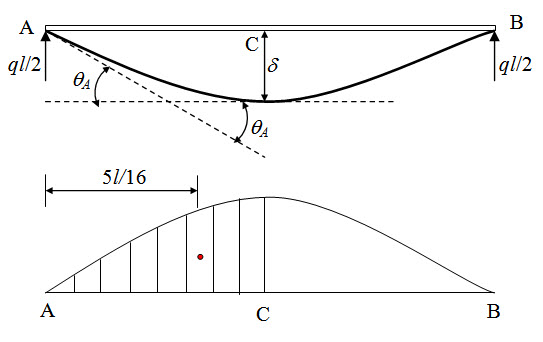
Due to symmetry slope of the elastic line at midspan is zero. Therefore

\[{\theta _{AC}} = {\theta _A} = \int\limits_{{x_A}}^{{x_C}} {{{{M_x}dx} \over {EI}}}={1 \over {EI}}\int\limits_0^{{{l/2}}} 2{\left( {{{ql} \over 2}x - {{q{x^2}} \over 2}} \right)dx}\]

\[\Rightarrow {\theta _A}={{q{l^3}} \over {24EI}}\]

Now since δ  may be considered as the deflection at A with respect to tangent at C, we have,

\[\delta={\theta _A}\bar x = {{5q{l^3}} \over {384EI}}\]

5.3 Example 2

A cantilever beam AB is subjected to a concentrated load P at its tip as shown in Figure 5.3. Determine deflection and slope at B.

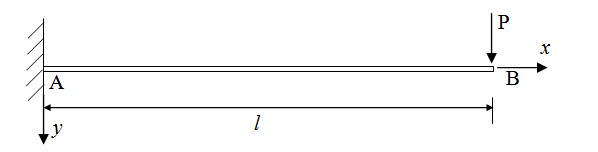Fig. 5.3.

 Solution

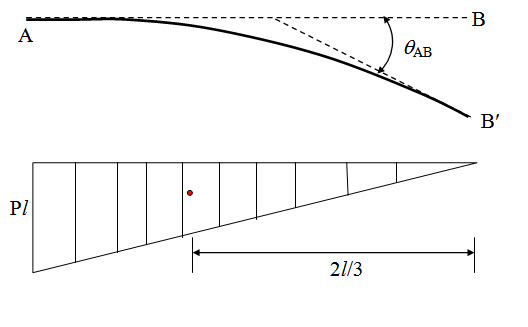
\[{\theta _{AB}}=\int\limits_{{x_A}}^{{x_B}} {{{{M_x}dx} \over {EI}}}={{P{l^2}} \over {2EI}}\]

Since slope at A is zero,

\[{\theta _B}={\theta _{AB}}=-{{P{l^2}} \over {2EI}}\]

\[\delta={\theta _B}\bar x={{P{l^2}} \over {2EI}}{{2l} \over 3}={{P{l^3}} \over {3EI}}\]

 

Suggested Readings

Hbbeler, R. C. (2002). Structural Analysis, Pearson Education (Singapore) Pte. Ltd.,Delhi.

Jain, A.K., Punmia, B.C., Jain, A.K., (2004). Theory of Structures. Twelfth Edition, Laxmi Publications. 

Menon, D. (2008), Structural Analysis, Narosa Publishing House Pvt. Ltd., New Delhi.

Hsieh, Y.Y. (1987), Elementry Theory of Structures , Third Ddition, Prentrice Hall.