Hydraulic Drive & Controls

LESSON 4. PASCAL’S LAW, FLOW, ENERGY, WORK AND POWER

4.2 Energy

Energy is the capacity of a body to do work. Hydraulic devices are able to do work on objects because hydraulic oil possesses energy. The total hydraulic energy consists of three different types of energy:

(i) Kinetic energy – due to motion

(ii) Potential energy – due to position

(iii) Pressure energy – due to condition of the fluid

4.3 Kinetic Energy

By definition, kinetic energy is energy possessed by a body by virtue of its motion. Kinetic energy is proportional to mass of a body and square of its velocity. Hence greater the velocity, greater is the kinetic energy. For example, when water is released from a dam, it moves at a very high velocity which represents the energy of motion or kinetic energy. The kinetic energy possessed by a body of mass ‘m’ moving with a velocity ‘v’ is given by:

\[K.E.\; = \;\frac{1}{2}m{v^2}\]                                                               (4.1)

where, if ‘m’ is in kg and ‘v’ is in ms^-1, then unit of K.E. is N-m or Joule (J).

Since mass, m = volume of liquid ‘V’ × density ‘r’

\[K.E.\; = \;\frac{1}{2}V\rho {v^2}\; = \;\frac{{V\rho {v^2}}}{2}\]

This is also called velocity pressure i.e. pressure caused by kinetic energy.

K.E. when expressed per unit weight is given by

\[\;\frac{{K.E.}}{{Weight}} = \;\frac{{\frac{1}{2}m{v^2}}}{{mg}}\; = \;\frac{{{v^2}}}{{2g}}\]                                                                            (4.3)

In SI units, v²/2g  is expressed in m.

4.4 Potential Energy

Potential energy is the energy of a body or a system due to the position of the body or the arrangement of the particles of the system. It is also called stored energy. An object has potential energy in proportion to its vertical distance above the ground surface. For example, water stored in a dam represents potential energy until it is released.  When a mass is lifted up, the force of gravity will act so as to bring it back down. Lifting the mass requires energy to perform work on the mass. According to the law of conservation of energy, energy can neither be created nor destroyed; energy can only be changed from one form into another. Thus the energy that went into lifting up the mass is stored in its position in the gravitational field i.e. as potential energy. If the mass is dropped, this stored energy will be converted into kinetic energy. The potential energy in a hydraulic system is the equivalent of the height ‘h’ of the liquid column in the system.

Potential Energy = mass  x  gravitational acceleration x  height

PE = mgh                                                                                                           (4.4)

Since the earth exerts a continuous gravitational pull on all objects of mass ‘m’, which we call weight ‘W’ = mg

PE = Wh                                                                                                       (4.5)

If ‘m’ is in kg, ‘g’ is in ms^-2 and ‘h’ is in m, then unit of P.E. is N-m or Joule (J).

P.E. when expressed per unit weight is given by

\[\;\frac{{P.E.}}{{Weight}} = \;\frac{{mgh}}{{mg}}\; = \;h\]                                                                                          (4.6)

Where ‘h’ is in m in SI units.

4.5 Pressure Energy

Pressure energy is the energy of a body by virtue of its condition. Pressure energy of a oil column of height ‘h’ is given by

\[\frac{P}{{\rho g}}\]                                                                                                                    (4.7)

Where ‘P’ is the pressure of oil column and ‘ρ’ is the oil density.

4.6 Work

Work is a measure of energy expanded. By definition, work done by a force is equal to the product of the force and the displacement of its point of application in the direction of force.

For example, a force ‘F’ applied by a person on a cart using a rope moves it through a distance ‘s’, Figure 4.1.

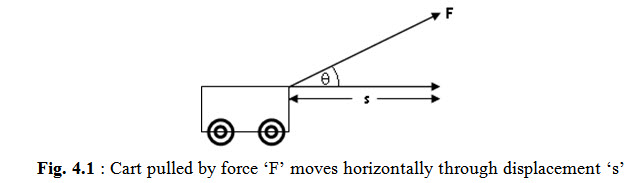
As the force ‘F’ has component Fcosθ in the direction of displacement ‘s’, work done is given by, W = Fcosθ × s

However if the force ‘F’ is applied along the displacement ‘s’, then θ = 0 and consequently cosθ = 1, then

W = F × s                                                                                                           (4.8)

In SI units, force is in Newton (N), displacement is in meter (m) and work done is measured in N-m or Joule (J).

4.7 Power

Power is the rate at which work is performed. It is defined as work done per unit time.

\[Power\; = \;\frac{{Work\;done}}{{Time\;Taken}}\]                                                                                        (4.9)

SI unit of power is Watt (W) which is equal to Js^-1.

Horse-power (hp) is widely used unit of power and 1 hp = 746 W

4.8 Units of Work and Power

Work can be considered as time integral of power. As electrical power is measured in kilowatt (kW), kilowatt-hour (kWh) is also used a unit of work or energy.

Work (Energy)

1 J        = 1 N-m

            = 0.102 kgf-m

            = 2.778 × 10^-7 kWh

            = 10⁷ erg (cgs unit)

Power

1 kW   = 1000 W

            = 102 kgf-m s^-1

            = 1.34 hp