Machine Design 3(2+1)

LESSON 13 DESIGN OF THREADED FASTNERS

13.1.1   Tensile Failure of Bolt

Maximum tensile stress induced in the bolt is given by,

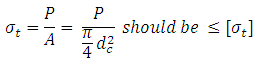
where, d_c = core diameter of the bolt. Cross-section at core diameter is the weakest section.

In addition to this, threads of the bolt can also fail in shear and crushing. For analysing that, it is assumed that each turn of the thread supports equal load and failure occurs in the threads of the bolt and not in the threads of the nut. Also stress concentration is neglected in the analysis of the bolts.

13.1.2    Shear Failure of Threads

Maximum shear stress developed in the threads is given by,

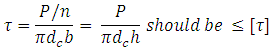
where  n = no. of turns, b = width of thread section at the root

            h = n×b = height of the bolt

13.1.3    Crushing Failure of Threads

Maximum crushing stress developed in the threads is given by,

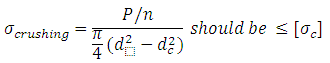
where  n = no. of turns, d = outer diameter of the bolt

13.1.4    Shear Failure of Bolt

In addition to the above case of tensile loading, bolts may also be subjected to shear loads. In such case the maximum shear stress is given by,

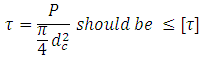
where P, in this case, is the force acting on the joint perpendicular to the axis of bolt.

Using above relations, core diameter of the bolt can be calculated for a given material and type of loading. If the standard tables of bolts are available, a suitable bolt can be selected and other dimensions can be taken from the table. If tables are not available approximate relation d_c = 0.8 d is generally used to find the nominal diameter of the bolt. (Exact relation for ISO metric threads is d_c = d – 1.22687 p, where p is the pitch).

13.2         Pre-stress in Bolts

Stress develops in the threaded joint because of initial tightening torque. Stress developed is compressive in the members and tensile in nature in the bolts. Value of initial tension in the bolts is calculated using an empirical relation.

Initial Tension,            F_i = 2840 d (N) (for fluid tight joints)

                                        = 1420 d (N) (for other joints)

where, d is nominal diameter of the bolt in mm. Initial Stress in the bolt can be calculated from F_i .

 

13.3          Eccentrically Loaded Bolted Joints

13.3.1    Eccentric Load acting in the plane of the Bolts

Figure 13.2                   Eccentric load acting in plane of bolts

Consider the joint shown in Figure 13.2. Let a force P is acting at a distance e from the centre of gravity. This eccentric force can be considered as equivalent to an imaginary force P acting at the centre of gravity and a moment ‘Pe’ about the centre of gravity.

Primary shear force developed in the bolts, because of the direct load,

Secondary shear force because of the moment can be determined as follows.

It is assumed that the secondary shear force in any bolt is proportional to its distance from the centre of gravity.

Considering C as a proportionality constant,

So,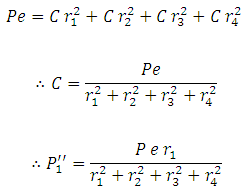                                          

Similarly P^"₂, P"3 and P"4 the values of , and can be calculated. Primary and secondary shear forces are then vectorially added to get the resultant shear force in each bolt, which can then be used to find the stresses.

13.3.2    Eccentric Load acting perpendicular to the plane of the Bolts

Figure 13.3                   Eccentric load acting perpendicular to the plane of bolts

Consider a bracket bolted to a structure as shown in Figure 13.3. Let an eccentric force P be acting at a distance e from the structure. Lower two bolts are denoted by 2 and upper two by 1. P is acting perpendicular to the axes of the bolts and leads to a direct shear load, which can be given by,

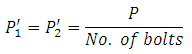
Also, because of eccentricity, P leads to a moment Pe, which tends to tilt the bracket about the edge C. This leads to resisting tensile forces in all the bolts, which are proportional to their distance from C. If  and  are the resisting tensile forces developed in bolts at position 1 and 2 respectively,

 

Considering C as a proportionality constant,

 

Equating the moments due to P and due to the resisting forces,

 

Or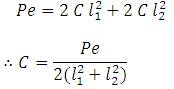                                             

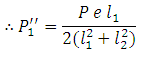and 

Bolts farthest from the tilting edge have maximum value of resisting tensile force. Therefore stresses in the bolts denoted by 1 will have maximum stresses which can be determined as follows:

Maximum principal stresses developed in the bolts can then be found and compared with the allowable values or bolt dimensions can be found for a given material.

13.3.3    Eccentric Load acting parallel to the plane of the  Bolts

Consider the bracket bolted to structure shown in Figure 13.4. Let an eccentric force P be acting at a distance e from the edge C about which it tends to tilt the bracket. There are two bolts at each position i.e. 1 & 2. As P, in this case, is acting parallel to the axes of the bolts, it leads to a primary tensile force and a secondary tensile force due to the moment.

Primary tensile forces are given by,

                       

Figure 13.4                   Eccentric load acting parallel to the plane of bolts

As discussed in the previous case, secondary tensile forces are given by,

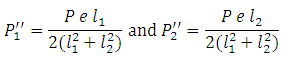
Total tensile force in each bolt at position 1 & 2 are given by,

P₁ = P^'₁ + P^"₂    and   P2 = P^'₂ + P^"₂

As bolts at 1 are farthest from the edge about which the bracket tends to tilt, maximum resisting force is developed in those. Maximum tensile stress in bolts at position 1 is given by,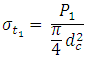

This can be compared with the allowable values of tensile stress.

References:

1. Design of Machine Elements by V B Bhandari

2. Analysis and Design of Machine Elements by Vijay Kumar Jadon

3. A Text Book of Machine Design by RS Khurmi