Site pages
Current course
Participants
General
Module 1: Formation of Gully and Ravine
Module 2: Hydrological Parameters Related to Soil ...
Module 3: Soil Erosion Processes and Estimation
Module 4: Vegetative and Structural Measures for E...
Keywords
Lesson 18 Modification of Universal Soil Loss Equation
18.1 Introduction
Soil erosion is an important term for consideration in the planning of watershed development works. It reduces not only the storage capacity of the downstream reservoirs but also deteriorates the productivity of the watershed due to the loss of fertile top soil. Accurate estimation of sediment-transport rates depends on an accurate a priori estimation of overland flows.
It is necessary to quantify soil erosion more extensively, with the aim of providing a tool for planning soil conservation strategies on watershed basis. The formulation of proper watershed management programs for sustainable development requires information on watershed sediment yield. Prediction of the sediment yield is difficult to measure because of the complexity of the variables involved in erosion modeling. The universal soil loss equation (USLE), the revised version of it (RUSLE), and its modified version (MUSLE) are used in hydrology for computing the amount of potential soil erosion and sediment yield.
The USLE (Wischmeier and Smith, 1978) was developed for estimation of the annual soil loss from small plots of an average length of 22 m. Its application for individual storm events and large areas leads to large errors. However, its accuracy increases if it is coupled with a hydrological rainfall-excess model (Novotny and Olem, 1994). In the USLE model, there is no direct consideration of runoff, although erosion depends on sediment being discharged with flow and varies with runoff and sediment concentration. It has been observed that delivery ratios to determine sediment yield from soil loss equation can be used to predict accurately but it varies considerably. The reason for this may be due to the variation in rainfall distribution over time from year to year.
18.2 Modified USLE
Williams (1975) modified the USLE to estimate sediment yield for a single runoff event. On the basis of that runoff is a superior indicator of sediment yield than rainfall; i.e., no runoff yields no sediment, and there can be rainfall with little or no runoff-Williams (1975) replaced the R (rainfall erosivity) factor with a runoff factor. His analysis revealed that using the product of volume of runoff and peak discharge for an event yielded more accurate sediment yield predictions, especially for large events, than the USLE with the R factor. The Modified USLE, or MUSLE, is given by the following (Williams, 1975):
S = 11.8 (Q × qp × A)0.56 × K × C × P × LS × CFRG
Where,
S = Sediment yield for a single event in (Mg),
Q = Total event runoff volume (m3),
qp = Event peak discharge (m3 s-1),
A = Area of the hydrologic response unit (HRU) (ha) and
K, LS, C, and P = USLE parameters and these are dimensionless.
CFRG = Coarse fragment factor, which is estimated as
CFRG = exp (−0.053 × Rock)
Where, Rock is % rock in the uppermost soil layer.
The MUSLE approach has been used to estimate sediment yield at various sites. Some errors, however, have been associated with both USLE and runoff model estimates, resulting in under- and over-prediction of sediment yield from various rainfall events and site-specific characteristics, and have led to various proposals to increase accuracy after regression analysis. The complexity of watershed systems has forced modelers and users to develop modified, calibrated or revised versions of the MUSLE. Due to errors associated with the classic USLE, especially those relating to topographic factors in terms of limited availability of data on steep slope gradients; it is still unclear how the USLE can be applied to complex slopes beyond the range of the extended model. Application of the MUSLE has not been documented. The structure of the MUSLE model has inherited some limitations from classic USLE, especially those related to slope steepness (S factor).
18.3 Revised USLE
The science of predicting soil erosion and sediment delivery has continued to be refined to reflect the importance of different factors on soil erosion and runoff. The Revised Universal Soil Loss Equation (RUSLE) has improved the effects of soil roughness and the effects of local weather on the prediction of soil loss and sediment delivery. The importance of estimating erosion and sediment delivery has long been recognized to plan for minimizing the pollution by sediments as well as the chemicals carried with soil particles. The visual effects of erosion include rills and gullies and sediment blockages found in culverts or drainage ditches. A well planned and engineered erosion control and/or water management plan will alleviate many concerns about construction site erosion and potential pollution. RUSLE is a science-based tool that has been improved over the last several years. RUSLE is a computation method which is used for site evaluation and planning purposes and to aid in the decision process of selecting erosion control measures. It provides an estimate of the severity of erosion. It also provides numbers to substantiate the benefits of planned erosion control measures, such as the advantage of adding a diversion ditch or mulch. For example, a diversion may shorten the length of slope used in calculating a LS factor. Also, the application of mulch will break raindrop impact and reduce runoff. This section provides a method to calculate soil loss. Following the step-by-step procedure will provide estimated erosion in terms of mass per unit area per year, which can be converted to the more usable unit. [If an electronic version is preferred, RUSLE, the computer model, is available from the Natural Resources Conservation Service, United States Department of Agriculture. The recent version (RUSLE-2) was released for implementation in 2003]. Currently, there is no method to predict soil loss from concentrated flow areas and gullies.
Soil losses on construction sites can be predicted by using the Revised Universal Soil Loss Equation (RUSLE). The equation is as follows:
For bare ground conditions of graded areas of construction sites
A = R*K*(LS)*C* P
Where:
A is the computed soil loss Mg ha−1 year-1.
R is the rainfall value reflecting the energy factor multiplied by the intensity factor.
EI is the abbreviation for energy and intensity and is called the Erosion Index. The energy component is related to the size of the raindrops while the intensity is the maximum intensity for a 30-minute interval and is measured in inches per hour. EI is frequently illustrated in graphs by showing the percent of EI that occurs within a period of days or months. From the index, one can determine the period when the most intense storms are likely to occur.
Example 1: Using the given information, determine the sediment yield from a storm with a total runoff volume of 120 m3 and a peak discharge of 5 m3/s.
Solution:
K = 0.33
LS = 0.697
C = 0.004
P = 0.5
(Q qp)0.56= (120 x 5)0.56 = (600)0.56= 36
S = 95 (Q × qp)0.56 × K × C × P × LS = P95 x 36 x 0.33 x 0.697 x 0.004 x 0.5 = 1.57 Mg.
Table 18.1, 2,3, show list of the cover factor C values for planted cover crops for erosion control at construction sites.
Table 18.1. Cover Factor C Values for Different Growth Periods for Planted Cover Crops for Erosion Control at Construction Sites
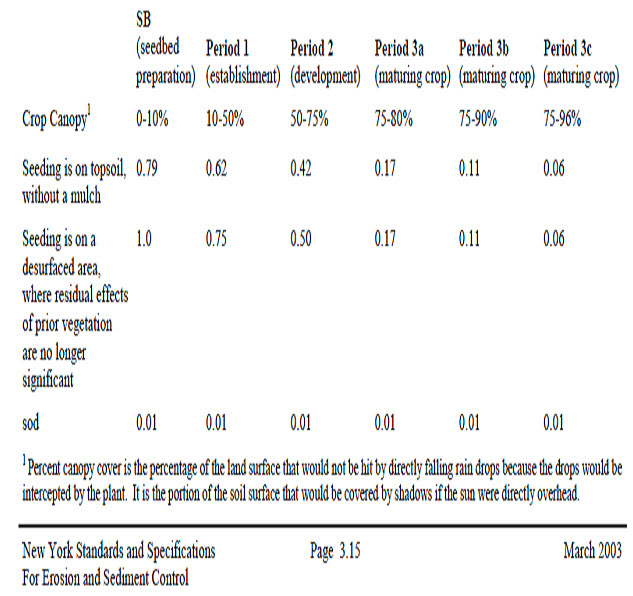
(Source: http://www.cdrpc.org/NET/WQ/ErosANDsed/3rusle.pdf)
Table 18.2. Cover Factor C value for Established Plants
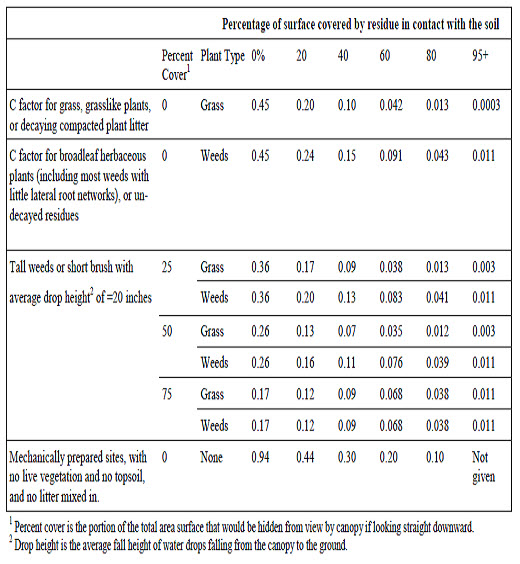
(Source: http://www.cdrpc.org/NET/WQ/ErosANDsed/3rusle.pdf)
Table 18.3 C factor value for different classes

(Source: http://www.msu.edu/~xuhui3/index_c.html)
Table 18.4 lists P factors for surface conditions on construction sites in relation to bare soils.
Table 18.4 conservation practice factor (P)

(Source: http://www.msu.edu/~xuhui3/index_c.html)
Example 2: In a 23 ha catchment, soil erosion is to be evaluated. The following information for the catchment is available. Calculate the soil loss.
R = 1000 (MJ-mm/ha) (mm/h) per year
K = 0.25 M/ha/R
LS = 0.1
Contour - farming in 13 ha (P = 0.6)
Strip cropping in 9 ha (P = 0.3)
Crops are maize and cowpea (assume weighted C= 0.5)
Solution:

Table 18.6. Summary of the differences between the USLE and RUSLE

(Source: http://ftp-fc.sc.egov.usda.gov/NCGC/products/nri/1997- 999nri/rusle.pdf)
18.4 Coupled SCS CN Method with USLE
The Soil Conservation Service curve number (SCS-CN) and Revised Universal Soil Loss Equation (RUSLE) models are widely used. A study incorporated antecedent moisture condition (AMC) in runoff production and initial abstraction of the SCS-CN model, and considered the direct effect of runoff on event soil loss by adopting a rainfall-runoff erosivity factor in the RUSLE model. The modified SCS-CN and RUSLE models were coupled to link rainfall-runoff-erosion modeling. The effects of AMC, slope gradient and initial abstraction ratio on curve number of SCS-CN, as well as those of vegetation cover on cover-management factor of RUSLE, were also considered. Three runoff plot groups covered by sparse young trees, native shrubs and dense tussock, respectively, were established in the Yang Juangou catchment of Loess Plateau. Rainfall, runoff and soil loss were monitored during the rainy season in 2008–2011 to test the applicability of the proposed approach. The original SCS-CN model significantly underestimated the event runoff, especially for the rainfall events that have large 5-day antecedent precipitation, whereas the modified SCS-CN model was accurate in predicting event runoff with Nash-Sutcliffe model efficiency (EF) over 0.85.
The SCS-CN method is based on the principle of the water balance and two fundamental assumptions (Mishra and Singh, 2002). The first assumption is that the ratio of direct runoff to potential maximum runoff is equal to the ratio of infiltration to potential maximum retention. The second assumption states that the initial abstraction is proportional to the potential maximum retention. The water balance equation and the two assumptions are expressed mathematically.