Soil & Water Conservation Structures 3(2+1)

Lesson 26. Phreatic Line in Earthen Dam

26.1 Locating Phreatic Line

It has been noticed from experiments that the line of seepage assumes more or less the shape of a parabola. The hydraulic gradient i is equal to the slope of the free surface and is constant with depth (Dupuit's theory), the resulting solution of the phreatic surface is parabola. In some sections a little divergence from a regular parabola is required particularly at the surfaces of entry and discharge of the line of seepage. The properties of the regular parabola which are essential to obtain phreatic line are depicted in Fig. 26.1.

Determination of Phreatic Line:

Before drawing the flow net for the earth dam section, it is necessary to plot the phreatic line more accurately. Following methods are used:

1. Casagrande’s graphical methods for determining phreatic line with and without horizontal drainage filter

2. Analytical methods for phreatic line for embankments with inclined discharge face without horizontal filter.

 Only graphical methods are discussed here

 26.1.1 Casagrande’s Graphical Method (with filter)

Casagrande assumed that the phreatic line is a base parabola whose focus is at F which is the starting point of the filter FE. To determine the phreatic line following procedure is followed:

 

 

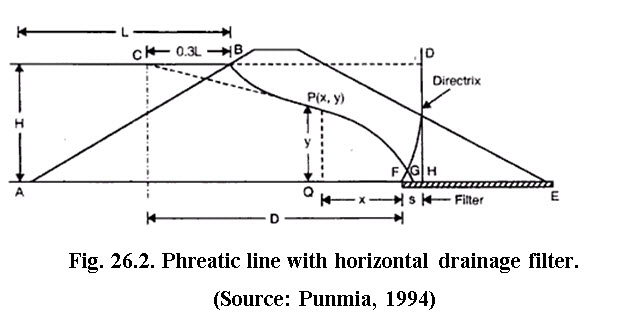
1. AB is the upstream face. Let its horizontal projection be L. On the water surface, measure a distance BC = 0.3 L. then the point Cis the starting point of base parabola (Fig. 26.2).

2. To locate the directrix of the parabola, use the principle that any point on the parabola is equidistant from the focus as well as from the directrix. Hence with point C as the centre and CF as the radius, draw an arc to cut the horizontal line through CB in D. Draw a vertical tangent to the curve FD at D. Evidently, CD = CF. hence the vertical line DH is the directrix.

3. The last point G on the parabola will lie midway between F and H.

4. To locate the intermediate points on the parabola use the principle that its distances from the focus and directrix must be equal. For example, to locate any point P, draw vertical line QP at any distance x from F. Measure QH. With F as the centre and QH as the radius, draw an arc to cut vertical line through Q in point P

5. Join all these points to get the base parabola. However, some correction is to be made at the entry point. The phreatic line must start from B and not from C. Hence the portion of the phreatic line at B is sketched free hand in such a way that it starts perpendicularly to AB, and meets the rest of the parabola tangentially without any kink. The base parabola should also meet the downstream filter perpendicularly at G.

 In order to find the equation of this parabola, consider any point P on it, with co-ordinates (x, y) with respect to the focus F as origin (Fig.. 26.2).

From property of parabola we have

 

 

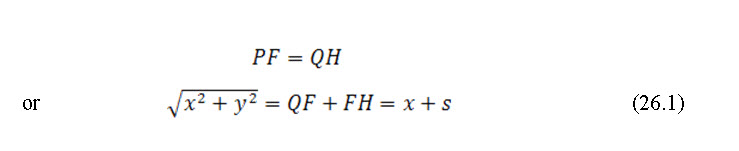
Where,  s = FH = focal distance

        

                                  

 

 

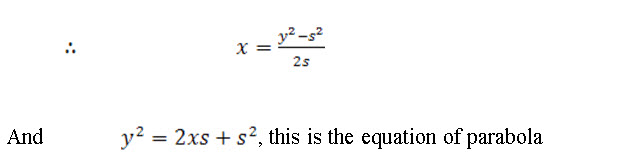
At C, x = D and y = H,

                            

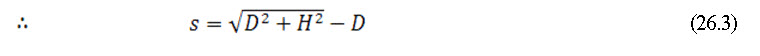
 Discharge through the body of dam: If q = discharge per unit length of dam

So we observe that through the vertical section PQ

                 

 

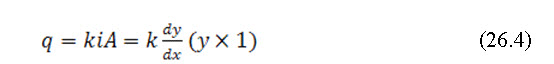
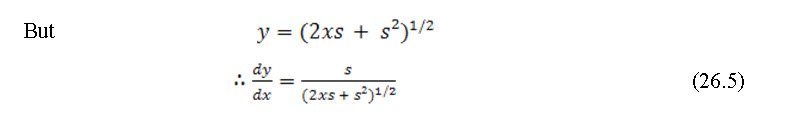
Substituting in (26.4), we get

                               

                                       

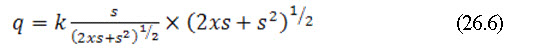
 This is the simple expression for discharge q in terms of focal distances.

 26.1.2 Casagrande Method for Embankment with Inclined Discharge Face (Without Filter)

In this case the base parabola BLG starts at C, which as before is at 0.3L, cuts drawdown slope at L and goes beyond the limits of the dam to meet the base line extended at G. The focus of the parabola is at F(Fig. 26.3), the lowest point of the slope. However, in practice the phreatic line must emerge to meet the downstream slope tangentially at N. The portion NF is called discharge face which always remains wet. The portion LN is the correction a by which the parabola is to be shifted downwards.

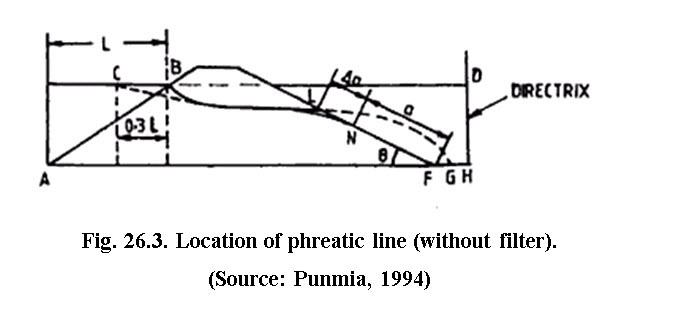
The values of also varies in different exit situations like homogeneous sections, position of rock toe vertical or inclined and horizontal filter, which is shown in Fig.26.4.

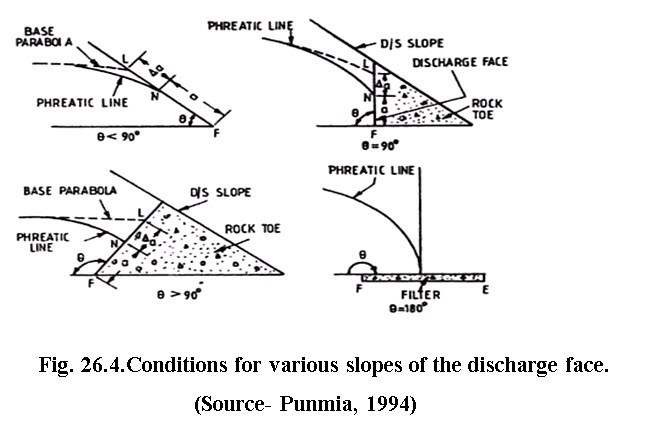
 Casagrande developed the following relationship for the values of slope  to determine a, from the known values of a which is shown in Fig.26.5.

                                               

Example 26.1:

For the earth dam of homogeneous section with a horinzontal filter as shown in Fig. 26.6, if the coefficient of permeability of the soil material used in the dam is 5 *10^-4 cm/sec., find the seepage flow per unit length of the dam.

 

Solution:

 

 

 The parabola cuts the reservoir water surface at C, such that

                   FC̕ = (140- 30 - 72) + 21.6 = 65.6 m

 And             CC̕  = 18 m

 The equation of the parabola is, therfore,

     

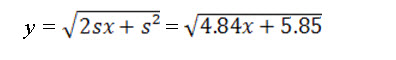
 the coordinate of the parabola are tabulated below:

x	0	10	20	30	40	50	60	65.6
y	2.42	7.36	10.11	12.30	14.1	15.7	17.25	18

Keywords: Seepage, Phreatic line, Earthen dam

References

• Das, B. M. (2007). Advanced Soil Mechanics, Third edition, Taylor & Francis.

• Das, G. (2008). Hydrology and Soil Conservation Engineering. PHI Learning PVT. LTD., New Delhi.

• Lambe, T.W. and Whitman, R.V. (1979). Soil Mechanics, SI Version, John Wiley & Sons, New York.

• Murthy V. N. S. (2002). Geotechnical Engineering. Principles and Practices of Soil Mechanics and Foundation Engineering", Marcel Dekker, Inc.,

• Punmia, B.C. (1994).Soil Mechanics and Foundations, Thirteenth Edition, Laxmi Publications (P) Ltd., New Delhi

• Suresh, R. (1993). Soil and Water Conservation Engineering. Standard Publishers and Distributors, New Delhi.

Suggested Readings

• Das, G. (2008). Hydrology and Soil Conservation Engineering. PHI Learning PVT. LTD., New Delhi.

• Murthy V. N. S. (2002). Geotechnical Engineering. Principles and Practices of Soil Mechanics and Foundation Engineering", Marcel Dekker, Inc.,

• Punmia, B.C. (1994). Soil Mechanics and Foundations, Thirteenth Edition, Laxmi Publications (P) Ltd., New Delhi

• Suresh, R. (1993). Soil and Water Conservation Engineering.Standard Publishers and Distributors,New Delhi.