Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 5. Stress in Soil
5.1 Concept of Effective Stress
The effective stress concept is very useful in soil mechanics to calculate shear strength, settlement, earth pressure. Figure 1 shows a soil sample whose top portion is dry or above water table (W.T) and bottom portion is fully saturated or below the water table. A point at any depth within the soil mass (say point ‘A’), the soil is subjected to stress due to the soil pressure above that level. The total stress (σ) acting at the point ‘A’ is:
\[\sigma={h_1}{\gamma _d} + {h_2}{\gamma _{sat}}\] (5.1)
where h1 and h2 are the thickness of the dry and saturated zone of the soil mass, respectively. \[\gamma\] d and \[\gamma\] sat are the dry and saturated unit weight of the soil. The unit of unit weight is ‘kN/m3’ and unit of thickness of the soil layer is ‘m’. Thus, unit of stress is ‘kN/m2’. The stress is defined as load per unit area. The stress at any point within the soil mass can be calculated by multiplying unit weight of the soil and thickness of the soil layer. The proper unit weight of the soil has to be used depending on the position of water table or nature of soil (i.e dry, partially saturated, fully saturated or submerged).
The total stress within the completely saturated soil has two parts: i) stress due to the pore water and called pore water pressure (as the pores of the soil solids are filled with water) and ii) stress due to the soil skeleton (or soil particles) and called effective stress. The pore water pressure (u) at a depth of h2 below ground water table (point ‘A’ in Figure 5.1) is determined by multiplying the height of water above the point and unit weight of water. Thus:
\[u={h_2}{\gamma _w}\] (5.2)
where \[\gamma\] w is the unit weight of the water (generally taken as 9.81 kN/m3 or 10 kN/m3). The effective stress (\[\sigma '\]) is equal to total stress minus pore water pressure. Thus,
\[\sigma=\sigma ' + u\] (5.3)
and
\[\sigma '=\sigma-u={h_1}{\gamma _d}+{h_2}{\gamma _{sat}}-{h_2}{\gamma _w}={h_1}{\gamma _d}+{h_2}({\gamma _{sat}}-{\gamma _w})= {h_1}{\gamma _d} + {h_2}\gamma '\] (5.4)
where \[\gamma '\] is the submerged unit weight of soil. Thus, for dry soil total stress and effective stress both are same (as for dry soil u =0) and can be determined by multiplying the thickness of soil layer and dry unit weight (\[\gamma_d\]) of the soil. In case of fully saturated soil, total stress can be determined by multiplying the thickness of soil layer and saturated unit weight (\[\gamma_sat\]) of the soil, whereas effective stress can be determined by multiplying the thickness of soil layer and submerged unit weight (\[\gamma '\]) of the soil. In case of partially saturated soil, total stress and effective stress both are same (as for partially saturated soil u =0) and can be determined by multiplying the thickness of soil layer and bulk unit weight (\[\gamma_t\]) of the soil. Generally soil below water table is considered as fully saturated soil and soil above water table is dry or partially saturated soil.
In case of partially saturated soil, soil pores are filled with water and air both. Thus, total stress has three component i) stress due to pore water and is called pore water pressure (uw) ii) stress due to pore air and is called pore air pressure (ua) and iii) stress due to the soil skeleton and called effective stress (s¢). The effective stress expression for partially saturated soil is:
\[\sigma '=\sigma-{u_a}+\chi ({u_a}-{u_w})\] (5.5)
where χ is a constant depends on the unit cross-sectional area of the soil occupies by the water. The value of χ varies in between 0 to 1. For dry soil, χ=0 and for completely saturated soil, χ=1. However, in general, for calculation purpose, the pore water pressure and pore air pressure of the dry and partially saturated soil are neglected.

Fig. 5.1. Pore water pressure measurement by stand pipe.
The total stress can be measured by pressure cell or pressure sensor and the pore water pressure can be measured by standpipe or piezometer. However, the effective stress can not be measured. As shown in Figure 1, if a stand pipe is inserted at any level within the soil mass below water table, the water level can be determined by observing the height upto which the water raises in the stand pipe. If effective stress increases the soil particles become denser. Thus, the void ratio and compressibility of the soil decreases which caused increase in the shearing resistance of the soil. An equal increase in the total and pore water pressure keeps effective stress constant. Thus, there will be very little (or no effect) on the soil particles.
5.2. Stress calculation in Soil
The following example shows the stress calculation at different level within the soil.
Problem 1: Calculate total, effective stress and pore water pressure at different level of the soil as shown in Figure 5.2.
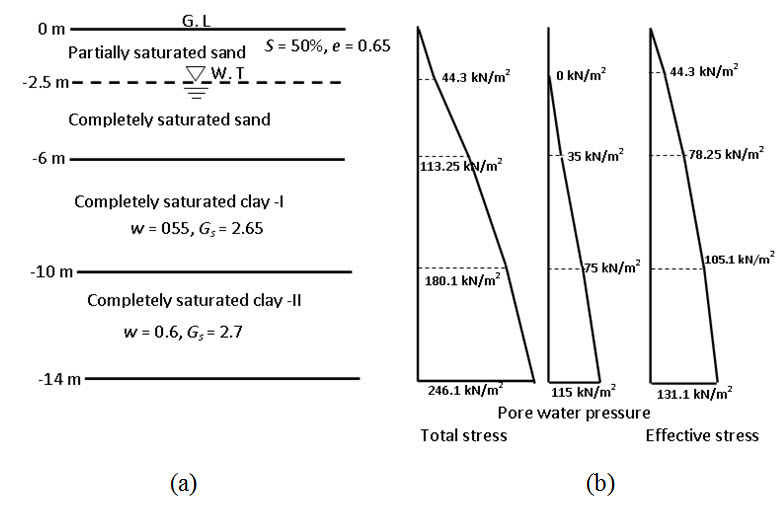
Fig. 5.2. (a) Soil profile (b) Stress diagrams
Solution:
The bulk unit weight of the partially saturated sand
\[{\gamma _{t(sand)}}={{{G_s} + Se} \over {1 + e}}{\gamma _w}={{2.6 + 0.5 \times 0.65} \over {1 + 0.65}} \times 10=17.72\;kN/{m^3}\]
The unit weight of the water is taken as 10 kN/m3. The saturated unit weight of sand is
\[{\gamma _{sat(sand)}}={{{G_s} + e} \over {1 + e}}{\gamma _w}={{2.6 + 0.65} \over {1 + 0.65}} \times 10=19.7\;kN/{m^3}\]
The saturated unit weight of the clay-I is.
\[{\gamma _{sat(clay - I)}}={{{G_s} + e} \over {1 + e}}{\gamma _w}={{{G_s} + {G_s}w} \over {1 + {G_s}w}}{\gamma _w}={{2.65 + 2.65 \times 0.55} \over {1 + 2.65 \times 0.55}} \times 10=16.71\;kN/{m^3}\]
[Se = Gsw and for fully saturated soil S =1]
The saturated unit weight of the clay-II is
\[{\gamma _{sat(clay - II)}}={{{G_s} + e} \over {1 + e}}{\gamma _w}={{{G_s} + {G_s}w} \over {1 + {G_s}w}}{\gamma _w}={{2.7 + 2.7 \times 0.6} \over {1 + 2.7 \times 0.6}} \times 10=16.49\;kN/{m^3}\]
At elevation -2.5 m
Total stress (σ) = 17.72 ´ 2.5 = 44.3 kN/m2
Pore water pressure (u) = 0
Effective stress () = 44.3 - 0 = 44.3 kN/m2
At elevation -6 m
Total stress (σ) = 17.72 ´ 2.5 + 19.7 ´ 3.5 = 113.25 kN/m2
Pore water pressure (u) = 10 ´ 3.5 = 35 kN/m2
Effective stress ( \[\sigma '\] ) = 113.25 - 35 = 78.25 kN/m2
At elevation -10 m
Total stress (σ) = 17.72 ´ 2.5 + 19.7 ´ 3.5 + 16.71 ´ 4 = 180.1 kN/m2
Pore water pressure (u) = 10 ´ 7.5 = 75 kN/m2
Effective stress ( \[\sigma '\] ) = 180.1 - 75 = 105.1 kN/m2
At elevation -14 m
Total stress (σ) = 17.72 ´ 2.5 + 19.7 ´ 3.5 + 16.71 ´ 4 + 16.49 ´ 4 = 246.1 kN/m2
Pore water pressure (u) = 10 ´ 11.5 = 115 kN/m2
Effective stress ( \[\sigma '\] ) = 246.1 - 115 = 131.1 kN/m2
References
Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Suggested Reading
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.