Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 7. Stress Under Loaded Area
7.1. Vertical stress under loaded area
Line Load: The vertical stress (σz) at point O (as shown in Figure 7.1) due to line load of intensity q/unit length can be determined as :
\[{\sigma _Z}=\frac{q}{z}\frac{2}{\pi}{\left[{\frac{1}{{1+{{\left({\frac{x}{z}}\right)}^2}}}}\right]^2}\] (7.1)
where z is the depth of the point O and x is the horizontal distance of the point O along X-axis.

Fig. 7.1. Vertical stress due to line load.
Strip Load: The vertical stress (σz) at point O (as shown in Figure 7.2) due to uniform strip load of intensity q/unit length can be determined as:
\[{\sigma _Z}={q \over \pi }(\alpha+\sin \alpha\cos 2\beta )\] (7.2)
where width of the load region is B. If b =0, i.e. vertical stress directly below the centre of the strip load can be determined as:
\[{\sigma _Z}={q \over \pi }(\alpha+ \sin \alpha )\] (7.3)
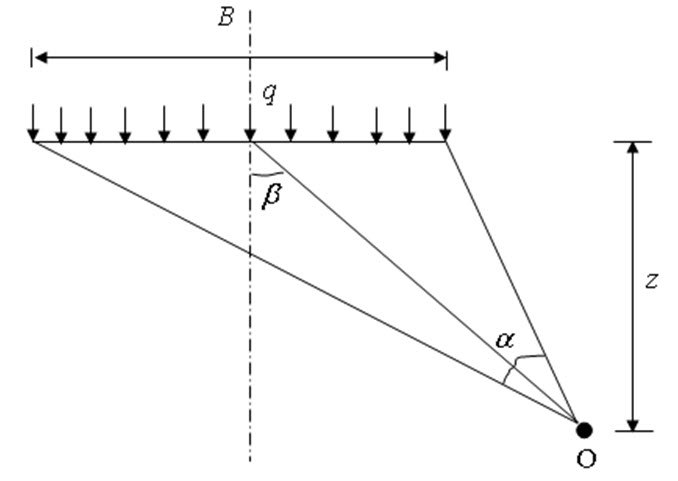
Fig. 7.2. Vertical stress due to strip load.
Uniformly loaded rectangular area: The vertical stress (σz) at any point O below the corner of a uniformly loaded rectangular area of intensity q (as shown in Figure 7.3) can be determined as:
\[{\sigma _z}=q{1 \over {4\pi }}\left[ {{{2mn\,{{({m^2} + {n^2} + 1)}^{{1 \over 2}}}} \over {{m^2} + {n^2} + 1 + {m^2}{n^2}}} \times {{({m^2} + {n^2} + 2)} \over {({m^2} + {n^2} + 1)}} + {{\tan }^{ - 1}}{{2mn\,{{({m^2} + {n^2} + 1)}^{{1 \over 2}}}} \over {{m^2} + {n^2} + 1 - {m^2}{n^2}}}} \right]\]
where m = L/z and n = B/z, L is the length of the loaded area and B is the width of the loaded area. The vertical stress at any point below the loaded area can be determined by dividing the rectangular loaded area into number of parts such that there will be a common corner point (the point of interest) for all the rectangles or squares.
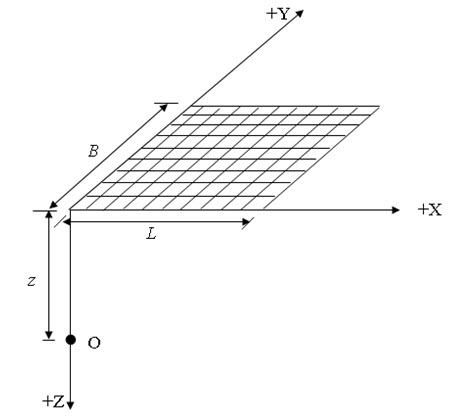
Fig. 7.3. Vertical stress under corner of a uniformly loaded rectangular area.
Uniformly loaded circular area: The vertical stress (σz) at any point O directly below the center of a uniformly loaded circular area of intensity q (as shown in Figure 7.4) can be determined as:
\[{\sigma _Z}=q\left[ {1-{{\left({\frac{1}{{1+{{\left({\frac{R}{z}}\right)}^2}}}}\right)}^{\frac{3}{2}}}}\right]\] (7.5)
where R is the radius of the circular loaded area and z is the depth of the point O.

Fig. 7.4. Vertical stress under centre of a uniformly loaded circular area.
References
Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Suggested Reading:
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.