Site pages
Current course
Participants
General
MODULE 1. Systems concept
MODULE 2. Requirements for linear programming prob...
MODULE 3. Mathematical formulation of Linear progr...
MODULE 5. Simplex method, degeneracy and duality i...
MODULE 6. Artificial Variable techniques- Big M Me...
MODULE 7.
MODULE 8.
MODULE 9. Cost analysis
MODULE 10. Transporatation problems
MODULE 11. Assignment problems
MODULE 12. waiting line problems
MODULE 13. Network Scheduling by PERT / CPM
MODULE 14. Resource Analysis in Network Scheduling
LESSON 2. CONSTRUCTION
2.1 Common Errors
There are three types of errors which are most common in network drawing, viz.,
(a) Formation of a loop, (b) Dangling, and (c) Redundancy.
(a) Formation of a loop: If an activity were represented as going back in time, a closed loop would occur. This is show in fig which is simply the structure of Fig (b) with activity B reversed in direction. Cycling in a network can result through a simple error or when while developing the activity plans, one tries to show the repetition of an activity before beginning the next activity.
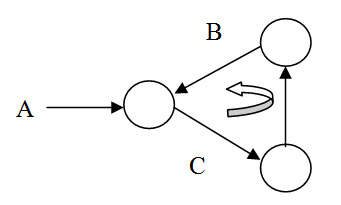
A closed loop would produce an endless cycle in computer programmes without a built-in routine for detection or i4-entification of the cycle; Thus one property of a correctly constructed network diagram is that it is "non-cyclic".
(a) Dangling: No activity should end without being joined to the end event. If it is not so, a dummy activity is introduced in order to maintain the continuity of the system. Such end-events other than the end of the project as a whole are called dangling events.
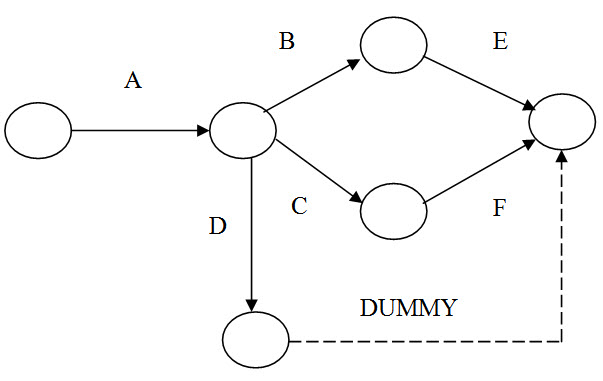
In the above network, activity D leads to dangling. A dummy activity is therefore introduced to avoid this dangling.
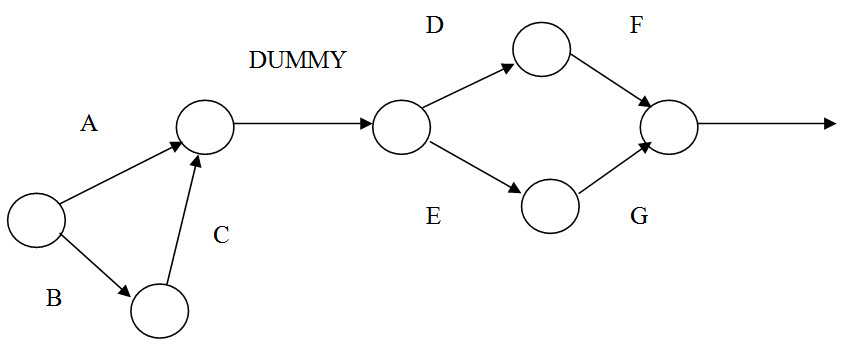
(c) Redundancy: If a dummy activity is the only activity emanating from an event, it can be eliminated. For example, in the network show in Fig the dummy activity is redundant and can be eliminated, and the network redrawn.
Rules of Network Construction
-
Each activity is represented by one & only one arrow so that no single activity can be represented twice in the network.
-
Time follows from left to right. Arrows pointing in opposite directions must be avoided.
-
Arrows should be kept straight and not curved or bent.
-
Use dummies freely.
-
Every node must have at least one activity preceding it and at least one activity following it, except that the beginning node has no activities before it and the ending node has no activities following it.
-
Only one activity may connect any two nodes. This rule is necessary so that an activity can be specified by giving the numbers of its beginning and ending nodes.
Numbering the Events
After the network is drawn in a logical sequence, every event is assigned a number. The number sequence must be such so as to reflect the flow of the network. In event numbering, the following rules should be observed:
Events numbers should be unique
Event numbering should be carried out an a sequential basis from left to right.
The initial event which has all outgoing arrows with no incoming arrow is numbered 0 or 1.
The head of an arrow should always bear a number higher than the one assigned at the tail of the arrow.
Gaps should be left in the sequence of event numbering to accommodate subsequent inclusion of activities, if necessary.
Example:
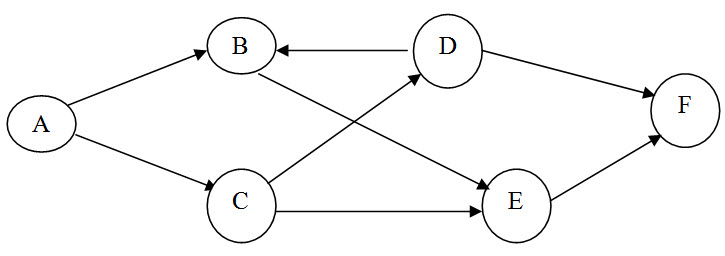
A television is manufactured in six steps, labeled A through F. Because of its size and Complexity, the television is produced one at a time. The production control manager thinks that network scheduling techniques might be useful in planning future production. He recorded the following information:
A is the first step and precedes B and C
C precedes D and E
B follows D and precedes E
F follows E
D is successor of F
(i) Draw an activity-on-node diagram for the production manager.
(ii) On checking with the records, the production manager corrects his last note to read, “D is a predecessor of F”. Draw a revised diagram of this network incorporating this new change.
Solution:
(a)
A is the first step which follows B and C
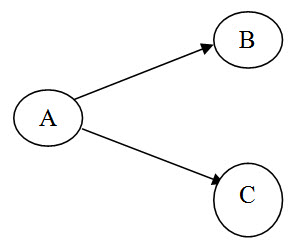
C precedes D and E
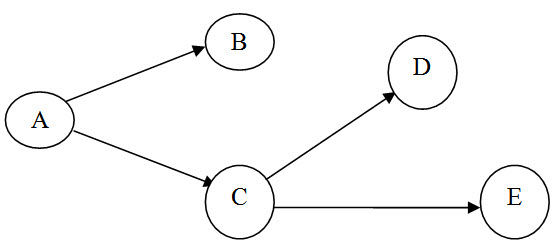
F follows E and D and is the successor of F
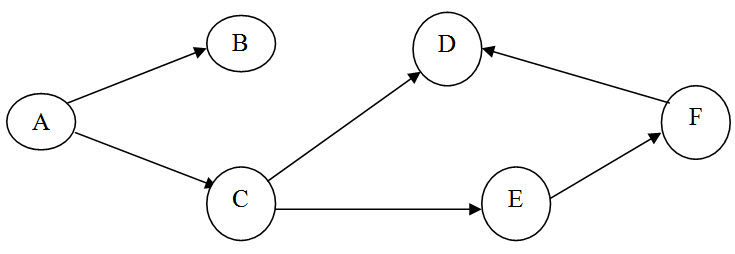
Now since B follows D and precedes E, the complete network diagram is shown below.
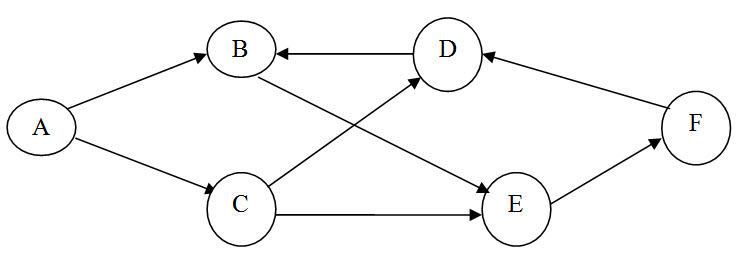
Evidently, this network contains a cycle as shown below

(b) Revised network when D is a predecessor of F is as follows: