System Engineering 3(3+0)

LESSON 5. Network Problems

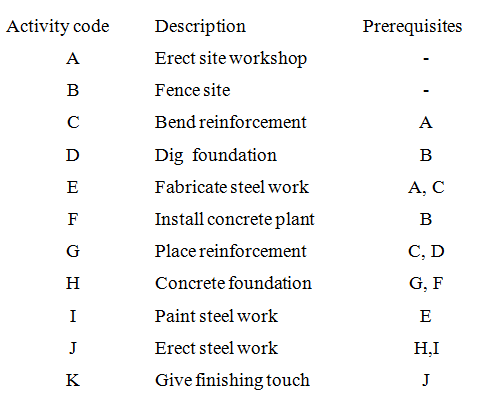Solution:

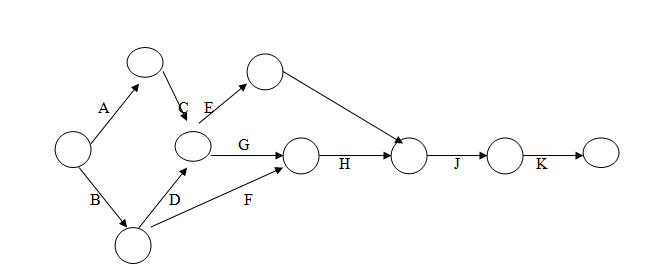
Problem 2. Construct the network diagram comprising activities B, C, .... Q and N such that the following constraints are satisfied:

B < E, F;   C < G, L;    E, G < H ;    F, G < H/;    L.H < I;

            L < M;   H, M < N;    H < J: I, J < P;    P < Q.

The notation X < Y means that the activity X must be finished before Y can begin.

Solution. The resulting network is shown in Fig. 27.6. The dummy activities D₁, D₂ and D₃ are used to establish the correct precedence relationships. D₄ is used to identify the activities I and J with unique end nodes. The nodes of the project are numbered such that their ascending order indicates the direction of progress in the project:

 

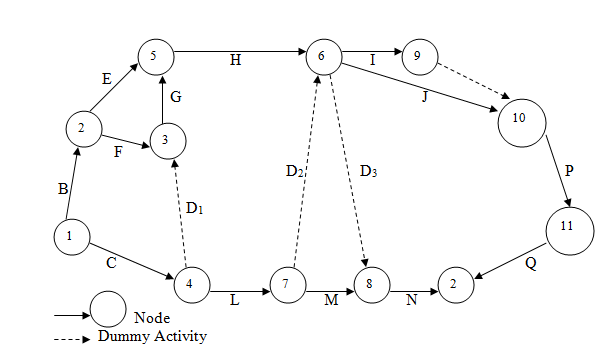
Problem 3. Construct the arrow diagram comprising activities A,  B, … and L such that the following relationships are satisfied:

(i) A, B, and C, the first activities of the project, can start simultaneously,
(ii)  A and B precede D, (iii) B precedes E, F and H, (iv) F and C precede G,
(v) E and H precede I and J,    (vi) C, D, F and J precede K,       (vii) K precedes L,

(viii) I, G and L are the terminal activities of the project.

Solution. The resulting network is shown in Fig. 27.7 below. The dummy activities are used to identify the activities A and B; E and H; C and F with a unique end node:

                                                               

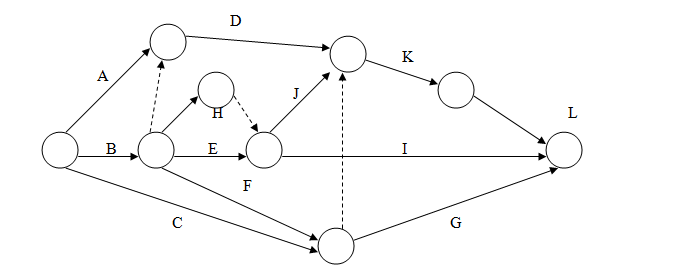
Problem 4. Draw a network for the following project and number the events according to Fulkerson's rules:

(1) A is the start event and K is the end event.                   (2) J is the successor event to F.
(3) C and D are successor events to B.                               (4) D is the preceding event to G.
(5) E and F occur after event C.                                          (6)  E precedes J

(7) C restrains the occurrence of G and G precedes H.       (8) H precedes J.

(9) F restrains the occurrence of H.                                     (10) K  succeeds event J.

Solution. The resulting network is shown in the figure given below. The dummy activity is used to identify the activities E and F with unique end node:

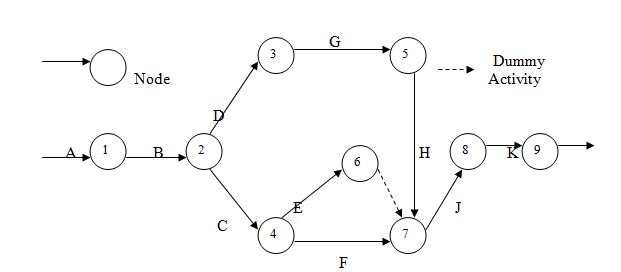
  The nodes of the network are numbered to indicate the direction of progress in the network

Problem 5. In a boiler overhauling project following activities are to be performed:

A. Inspection of boiler by boiler engineer and preparation of list of parts to be replaced/repaired.
B. Collecting quotations for the parts to be purchased.
C, Placing the orders and purchasing.
D. Dismantling of the detective parts from the boiler.
E. Preparation of necessary instructions for repairs.

F. Repair of parts in the workshop.
G. Cleaning of the various mountings and fittings.

H. Installation of the repaired parts
I. Installation of the purchased parts.        

J. Inspection.
K. Trial run.

       Assuming that the work is assigned to the boiler engineer who has one boiler mechanic and one boiler attendant at his disposal, draw a network showing the precedence relationships.

Solution. Looking at the list of activities, we note that activity A (inspection of boiler) is to be followed by dismantling of defective parts (D) and only after that it can be decided which parts can be repaired and which will have to be replaced. Now the repairing and purchasing can go side by side. But the instructions for repairs may be prepared after sending the letters for quotations. Note that it becomes a partial constraint, also started after activity D. Now we assume that repairing will take less time than purchasing. But the installation of repaired parts can be started only when the cleaning is completed. This results in the use of a dummy activity. After the installation of repaired parts, installation of purchased parts can be taken up. This will be followed by inspection and trial run.

The network showing the precedence relationships is given below:

 

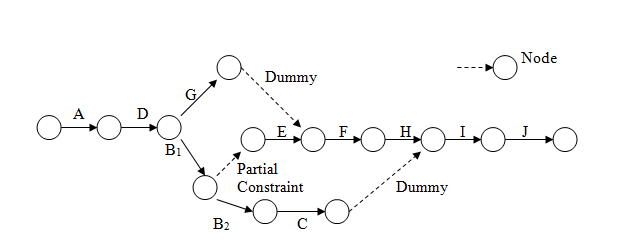
The dummy activities are used to identify the activities C, H and E, G with unique end nodes.

 

Problem 6. A television is manufactured in six steps, labelled A through F. The television is produced one at a time. The manager thinks that network scheduling will improve the position. It is noted that A is the first step and A < B. A < C, C < D, C < E, B > D, B < E, F > E, D is a successor of F.

(a) Draw an activity node diagram and identify the cycle.

(b) If D precedes F, show that the cycle gets eliminated.

(c) If the activities take occupy time as indicated:

A — 1 hours, B — 3 hours, C — 2 hours, D — 1 hour, E — 3 hours and F — 2 hours, determine the minimum time required to complete the television set.

 

Solution, (a) Using given constraints, the activity node diagram (network) is shown in Fig. 27.70. The dummy activities are introduced to establish the correct precedence relationships:

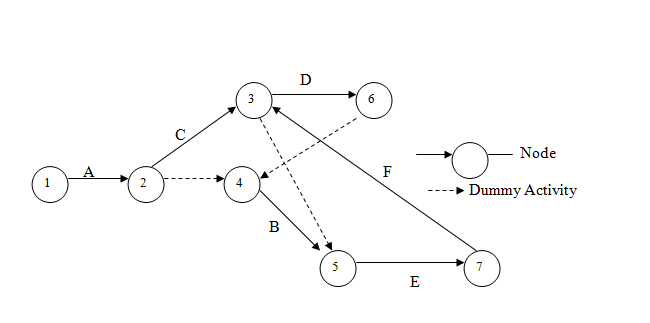
The nodes are numbered in such a way that their ascending order indicates the direction of progress in the manufacturing process. Among the various activities involved, obviously we have the following cycle: B→ E→ F→D→B.

(b) If D precedes F, the revised network is as shown below

 

 

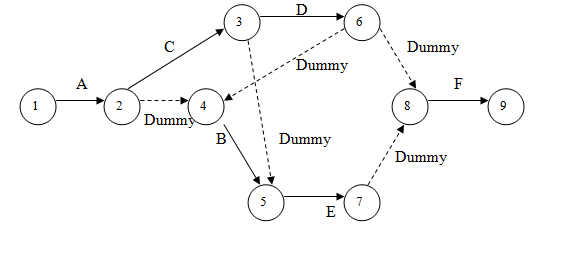
c) To determine the minimum time of completion of the project, we compute ESi and LFj for each activity of the project (TV set). The critical path calculations as applied to Fig. 27.11 are:

 ES₁, = 0                ES₂ = ES₁ + t₁₂ = 0 + 1 = 1        ES₃ = ES₂ + t₂₃= 1+2=3

 ES₆ = ES₃ + t₂₆ = 3 + 1 = 4   ES₄ =  Max {ES_i + t_i4} = Max. {1 + 0, 4 + 0} = 4

                                                               _{i =  2, 6}

 ES₅ =  Max.Es_i + t_i5} = Max. {3 + 0, 4 + 3} = 7  ES₇ = ES₅ + t₅₇ = 7 + 3 = 10
                 _{i = 3,4}

ES₈ =   Max.{ES_i + t_i8} = Max. {4 + 0, 10 + 0} = 10  ES₉ = ES₈ + t₈₉ =10 + 2 = 12.

                   _{i = 6, 7}

 The values of LF_j are similarly computed as follows:

LF₉ = ES₉ = 12                                         LF₈ = LF₉ – t₈₉ = 12 - 2 = 10
LF₇ = LF₈- t₇₈ = 10 - 0 = 10                    LF₅ = LF₇ – t₅₇ = 10 - 3 = 7
LF₄ = LF₅ - t₄₅ = 7 - 3 = 4                      LF₆ = Min. {10 - 0, 4 - 0} = 4
LF₃ = Min. {4 - 1, 7 - 0} = 3                  LF₂ = Min. {3 - 2, 4 - 0} = 1
LF₁ = LF₂ – t₁₂ = 1 - 1 = 0.

For determining the critical nodes, calculations are displayed in the following table:

Activity	Normal time    (hours)	Earliest	time	Latest	time	Total float
		Start	Finish	Start	Finish
(1. 2)	1	0	1	0	1	0
(2, 4)	0	1	1	4	4	3
(2,3)	2	I	3	I	3	0
(3,6)	1	3	4	3	4	0
(6, 4)	0	4	4	4	4	0
(4, 5)	3	4	7	4	7	0
(3, 5)	0	3	3	7	7	4
(5,7)	3	7	10	7	10	0
(7, 8)	0	10	10	10	10	0
(6, 8)	0	4	4	10	10	6
(8, 9)	2	10	12	10	12	0

 

      It is apparent from the table that the critical nodes are for the activities (1, 2), (2, 3), (3, 6), (6, 4), (4, 5), {5, 7), (7, 8) and (8, 9).

    The critical path, therefore, comprises the activities A, C, D, B, E and F, which is shown below

 

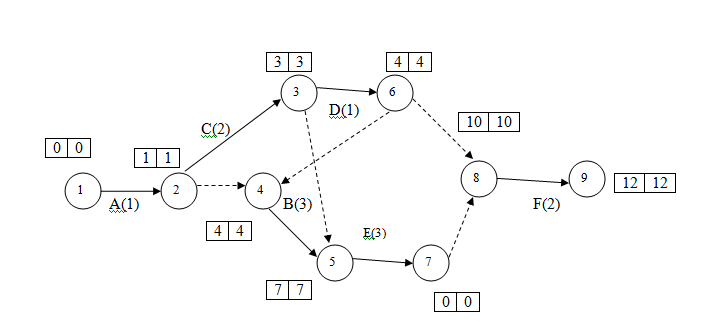
The Critical path is 1­­­­­­­-2-3-6-4-5-7-8-9                                                 

The minimum time required to complete the television set is  1+2+1+3+3+2 = 12 hours.