Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 25. Earth Pressure
25.1 Introduction
The soil that is retained by various structures like retaining walls, sheet piles (as shown in Figure 25.1) exerts a force on those structures. This force is called the earth pressure and the material that is retained by the structures is referred as backfill. Based on the wall movement, the earth pressure is classified as:
(i) Earth pressure at rest
(ii) Active earth pressure
(iii) Passive earth pressure
In case of a rigid and unyielding retaining wall, soil mass is in rest condition and no deformation or displacement is occurred in the wall. The earth pressure under this condition is called earth pressure at rest. If a retaining wall rotates about its toe and moving way from the backfill (as shown in Figure 25.2), the soil mass expends which causes reduction of the earth pressure on the wall. The earth pressure under this condition is called active earth pressure. On the other hand if a retaining wall moves towards the backfill (as shown in Figure 25.2), the soil is compressed and the earth pressure on the wall increases. The earth pressure under this condition is called passive earth pressure. Thus, the passive earth pressure is more than the earth pressure at rest and the earth pressure at rest is more than the active earth pressure.
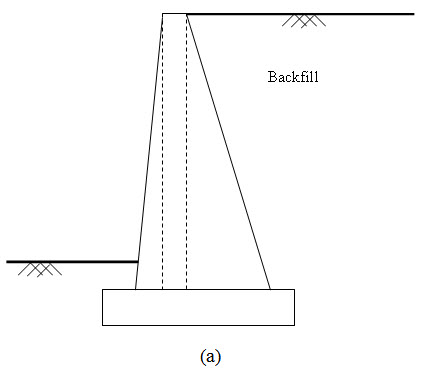
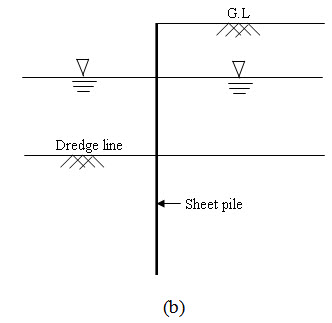
Fig. 25.1. Earth pressure acting on structure like (a) retaining wall (b) sheet Pile.
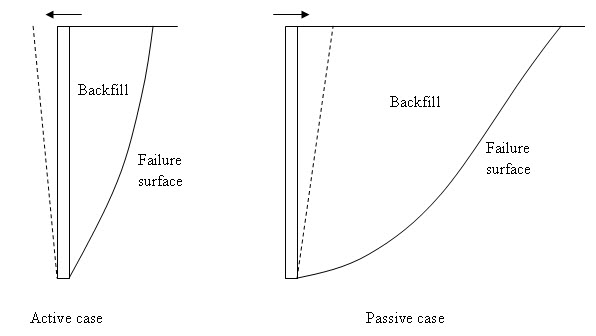
Fig. 25.2. Active and Passive earth pressure.
25.2 Earth Pressure at rest
The earth pressure at rest per unit length at a depth of z from the ground surface is expressed as:
\[{p_0}={K_0}\,\gamma \,z\] (25.1)
where \[\gamma\] is the unit weight of the soil, K0 is the coefficient of earth pressure at rest. Thus, the earth pressure is zero at the top of a retaining wall and at the base of the wall is K0\[\gamma\] H (if H is the height of the wall). The total force per unit length at rest condition acting on a retaining wall of height H is expressed as:
\[{P_0}={1 \over 2}{K_0}\,\gamma \,{H^2}\] (25.2)
The force (P0) will act at a height of H/3 from the base of the wall.
For sand and normally consolidated clays, the value of K0 is determined as (Jaky, 1944):
\[{K_0}=1-\sin \varphi\] (25.3)
where ø is the angle of friction of the soil. For over consolidated soil the K0 is expressed as:
\[{K_0}={K_{0(nc)}}\sqrt {OCR}\] (25.4)
where OCR is the over consolidation ratio.
References
Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New
Age International Publisher, New Delhi, India.
Suggested Readings
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
Murthy V.N.S (1997) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.