Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 26. Rankine’s Theory of Earth Pressure
26.1 Introduction
The assumptions of Rankine theory are:
(i) Semi-infinite mass of soil bound by a horizontal surface
(ii) Wall surface is vertical and smooth
(iii) Soil homogeneous, dry and cohesionless
However, the theory is extended for cohesive and submerged soils also. The failure surface for active case and passive case makes an angle of (45°+\[\phi\]/2) and (45°-\[\phi\]/2), respectively (as shown in Figure 26.1).

Fig. 26.1. Failure surface of active and passive case.
26.2 Earth Pressure on Retaining Wall
26.2.1. Cohesionless Backfill
Figure 26.2 shows a retaining wall with horizontal backfill with angle of internal friction \[\phi\] and effective unit weight \[\gamma\]'. The height of the wall is H. From Rankine’s theory, the active earth pressure (pA) at a depth of Z can be written as:
pA=KA\[\gamma\]'Z (26.1)
where KA is the active earth pressure coefficient and can be expressed as:
\[{K_A}={{1 - \sin \phi } \over {1 + \sin \phi }}\] (26.2)
Thus, the active earth pressure acting at the base of the wall is KA\[\gamma\]'H. The total active forces/unit length can be expressed as:
\[{P_A}={1 \over 2}{K_A}\gamma '{H^2}\] (26.3)
The force is acting at a height of H/3 from the base of the wall.
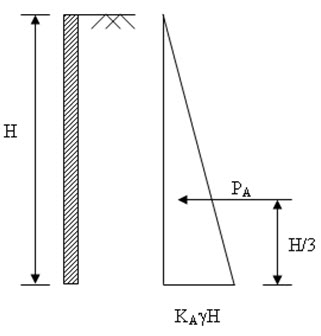
Fig. 26.2. Active pressure acting on retaining wall with horizontal backfill.
For passive case, the passive force/unit length can be expressed as:
\[{P_P}={1 \over 2}{K_P}\gamma '{H^2}\] (26.4)
where KP is the coefficient of passive earth pressure and can be expressed as:
\[{K_P}={{1 + \sin \phi } \over {1 - \sin \phi }}\] (26.5)
The passive force is also acting at a height of H/3 from the base of the wall. Figure 26.3 shows the effect of water table on the active earth pressure. The height of the wall is H and the position of the water table is at a depth of H1 from the ground surface. The active stress acting at the base of the wall is
pA = KA\[\gamma\]H1 + KA\[\gamma\]'(H-H1) + \[\gamma\]w(H-H1) (26.6)
\[{P_{A1}}={1 \over 2}{K_A}\gamma 'H_1^2\] (26.7)
\[{P_{A2}}={K_A}\gamma {H_1}(H - {H_1})\] (26.8)
\[{P_{A3}}={1 \over 2}\left\{ {{K_A}\gamma '(H - {H_1}) + {\gamma _w}(H - {H_1}} \right\}(H - {H_1})\] (26.9)
The resultant fore will act at a distance of Zc from the base of the wall. Thus,
\[{Z_c}={{{P_{A1}}\left( {H - {H_1} + {{{H_1}} \over 3}} \right) + {P_{A2}}\left( {{{H - {H_1}} \over 2}} \right) + {P_{A3}}\left( {{{H - {H_1}} \over 3}} \right)} \over {{P_{A1}} + {P_{A2}} + {P_{A3}}}}\] (26.10)
Figure 26.4 shows the active earth pressure for surcharge of intensity q/unit area on the ground surface. In such case earth pressure is constant through out the retaining wall. The active force/unit length can be expressed as:
\[{P_A}={K_A}qH\] (26.11)
In this case PA is acting at a height of H/2 from the base of the wall.
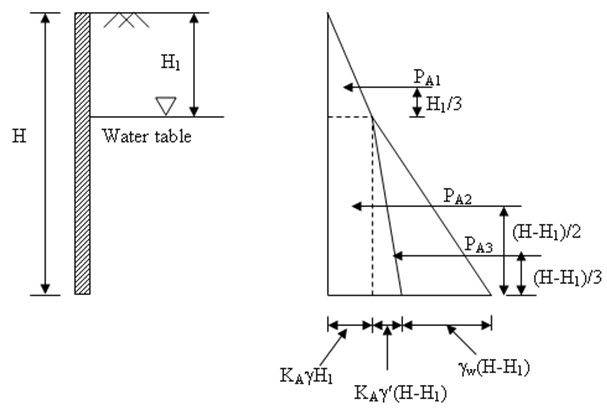
Fig. 26.3. Effect of water table on active earth pressure.
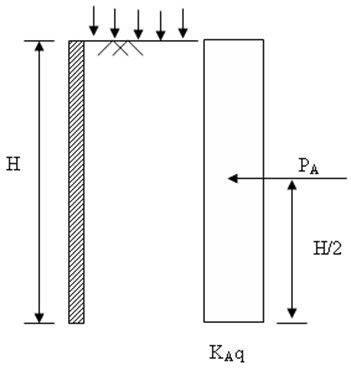
Fig. 26.4. Effect of surcharge.
Figure 26.5 shows a retaining wall with inclined backfill. The active pressure at a depth of Z can be written as:
pA=KA\[\gamma\]Z cosi (26.12)
where \[{K_P}={{\cos i - \sqrt {{{\cos }^2}i - {{\cos }^2}\phi } } \over {\cos i + \sqrt {{{\cos }^2}i - {{\cos }^2}\phi } }}\] (26.13)
The total active force/unit length can be expressed as:
\[{P_A}={1 \over 2}{K_A}\gamma \,{H^2}\cos i\] (26.14)
Similarly for inclined backfill, Kp can be expressed as:
\[{K_P}={{\cos i + \sqrt {{{\cos }^2}i - {{\cos }^2}\phi } } \over {\cos i - \sqrt {{{\cos }^2}i - {{\cos }^2}\phi } }}\] (26.15)
The total passive force/unit length can be expressed as:
\[{P_P}={1 \over 2}{K_P}\gamma \,{H^2}\cos i\\ (26.16)
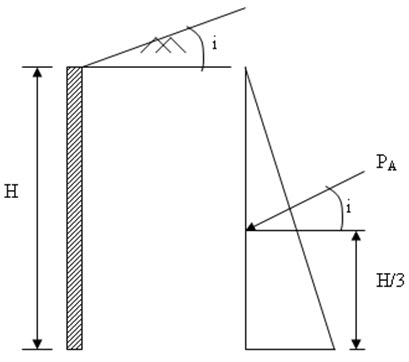
Fig. 26.5. Active earth pressure for inclined backfill.
References
Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Suggested Readings
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.