Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 29. Method for Stability Analysis
29.1 Finite Slope
There are three types of slope failure such as (as shown in Figure 29.1):
Slope Failure: In this type of failure, failure surface intersects the slope above the toe. It occurs when slope angle is high and soil close to toe is strong and soil in the upper part of the slope is strong.
Toe Failure: Most common type of failure. In this type of failure, failure surface passes trough the toe. It occurs for steep slopes and when soil above and below the base is homogeneous.
Base failure: In this type of failure, failure surface passes below the toe. It occurs for flat slopes and when soil below the base is relatively week.
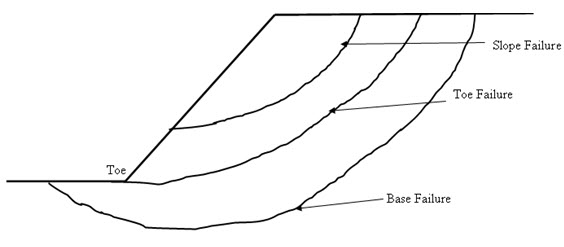
Fig. 29.1. Various failure surfaces.
29.2 Method of Slices
The stability of a slope can be analyzed by method of slices or Swedish Circle Method. In this method, the mass above the failure surface is divided into number of vertical slices of equal width (as shown in Figure 29.2). Considering a particular slice (slice number 5):
Driving force = T = W sina (29.1)
Resisting force = c'l + N tanø'
= c'l + W cosa tanø' (29.2)
where l is the length of the failure surface in each slice, c' is the effective cohesion of the soil, ø' is the effective internal friction angle of the soil, N is the normal force acting on each slice (as shown in Figure 29.2), a is the angle each slice is making with horizontal, W is the weight of each slice (W = \[\gamma\] b h), \[\gamma\] is the unit weight of the soil, b is the width of each slice, h is the average height of each slice.
Thus, driving moment for slice number 5 = R W sina (29.3)
Resisting moment = Rc'l + RW cosa tanø' (29.4)
he overall driving moment = \[R\sum\limits_{i = 1}^n {{W_i}\sin {\alpha _i}}\] (29.5)
The overall resisting moment = \[Rc'\sum\limits_{i=1}^n{{l_i}}+R\tan \phi'\sum\limits_{i = 1}^n {{W_i}\cos{\alpha _i}}\]
= \[Rc'L + R\tan \phi '\sum\limits_{i = 1}^n {{W_i}\cos {\alpha _i}}\] (29.6)
where n is the number of slice, L is the total length of the failure surface. Thus, the factor of safety against sliding (F) can be written as:
\[F={{Overall\;{{\rm Re}\nolimits} sisting\;Moment} \over {Overall\;Driving\;Moment}}\]
\[F={{c'L + \tan \phi '\sum\limits_{i = 1}^n {{W_i}\cos {\alpha _i}} } \over {\sum\limits_{i = 1}^n {{W_i}\sin {\alpha _i}} }}\] (29.7)
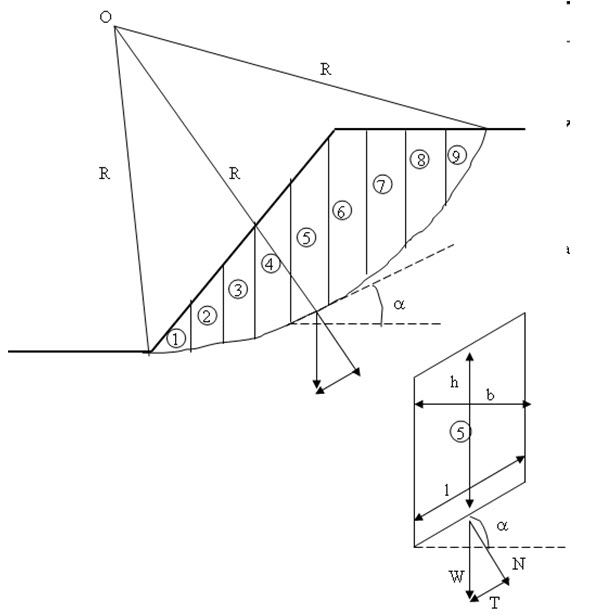
Fig. 29.2. Method of slices.
Considering effect of pore water pressure, the factor of safety can be written as:
\[F={{c'L + \tan \phi '\sum\limits_{i = 1}^n {({N_i} - {u_i})} } \over {\sum\limits_{i = 1}^n {{T_i}} }}\] (29.8)
where u is the resultant pore water pressure at the base of the slice.
References
Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Suggested Readings
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.