LESSON 7. Centroid of a Quadrant of a Circle

7.1 INTRODUCTION

The force of attraction of the earth for a particle is called the weight of particle. A body consists of a number of particles each of which has a weight or force of attraction directed towards the centre of the earth. The resultant of this parallel system of gravitational forces in space is the weight of the body.

  • The resultant weight does, however, pass through one point in the body, or the body extended, for all orientations of the body, and this point is defined as the centre of gravity or centre of mass for the body.

In the case of plane figures, the notion of centre of gravity can be modified as centroid of the plane figure. Hence, the centroid may be defined as that point through which the total area of the given figure may be imagined to be acting.

  • The difference between centre of gravity and centroid is that the centre of gravity applies to the bodies with mass and weight, while the centroid refers to the plane areas, lines and volumes of the body. 

The position of the centroid of a plane area is defined analytically with reference to the coordinate axes as shown in Fig.7.1:

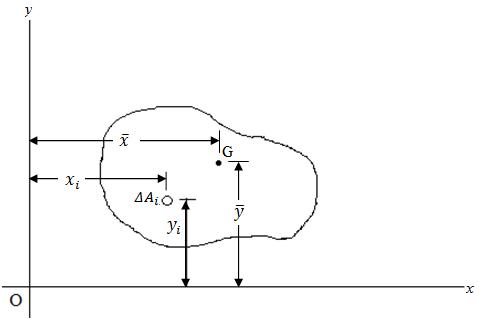
Module 3 Lesson 7 Fig.7.1 Centroid of plane figure

Fig.7.1 Centroid of plane figure

Let ΔAi be the area of an elemental part of plane figure having total area A and xi, yi be the coordinates of the centre of the element with respect to the coordinate axes as shown in figure. The centroidal coordinates of the total area are given as:

\[\bar x\]  = \[{{\sum \nolimits^ \left( {\Delta {A_i}{x_i}})} \over {\sum \nolimits^ \left( {\Delta {A_i}})}}\]                        (7.1a)

\[\bar y\]  = \[{{\sum \nolimits^ \left( {\Delta {A_i}{y_i}})} \over {\sum \nolimits^ \left( {\Delta {A_i}})}}\]                         (7.1b)

The summations indicate the inclusion of all elements of the area within the boundary of the area. When the elements are considered to be of sizes, which are smaller and smaller, the equation (7.1) becomes

\[\bar x\] = \[{{\smallint xdA} \over {\smallint dA}}\]      (7.2a)

\[\bar y\] = \[{{\smallint ydA} \over {\smallint dA}}\]      (7.2b)

The numerators of equations (7.1) and (7.2) are called the first moments of areas. That is

∑ (ΔAixi) = ∫xdA is called the first moment of area about y-axis and is denoted by Qy and ∑(ΔAiyi) = ∫ydA is called the first moment of area about x-axis Qx. The denominator is the total area of the plane figure A. Therefore, Eq. (7.2) can be written as

\[\bar x\] = \[{{Qy} \over A}\]          (7.3a)

\[\bar y\] = \[{{Qx} \over A}\]          (7.3b)

If the plane area is made up of composite parts consisting of geometrical figures such as rectangle, triangle, circle etc. then the centroid of such composite plane figures is obtained from:

\[\bar x\] = \[{{\sum{A_i}{x_i}} \over {\sum{A_i}}}\]          (7.4a)

\[\bar y\] = \[{{\sum{A_i}{y_i}} \over {\sum{A_i}}}\]          (7.4b)

Equations (7.1) – (7.4) can be used to determine the centroid of any plane area.

7.2 CENTROID OF A TRIANGLE

Module 3 Lesson 7 Fig. 7.2 Centroid of a Triangle

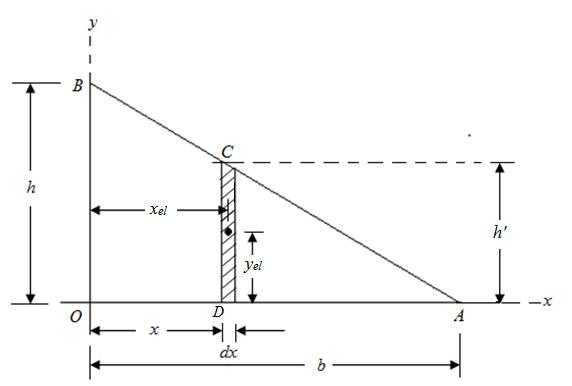
Fig. 7.2 Centroid of a Triangle    

Let us consider a triangular plane area of width b and height h as shown in Figure 7.2. Taking a differential strip of thickness dx and depth hꞌ at a distance x from O as shown, the area of the strip is given as

dA = hꞌ × dx                                                                (7.5a)

The height hꞌ can be expressed in terms of h and b from similar triangles OAB and DAC as                  

                                                         hꞌ =  (b-x)                                                                  (7.5b)

Substituting Eq. (7.5b) into Eq. (7.5a) yields

 dA =   (b-x) dx                                                           (7.5c)

 

The coordinates of the centre of the elemental strip are xel = x and yel = hꞌ/2. The first moments of the elemental strip about x and y axes are respectively given as

dQx = ydA = hꞌ dx = h2/2b2 (b-x2) dx      (7.5d)

dQy = xdA = x hꞌdx =  (b-x) xdx                 (7.5e)

To determine the centroidal coordinates of the triangle OAB, Eqs. [7.5(c), (d) and (e)] are substituted in Eq. (7.2) and integrated between the limits of x from 0 to b.

Module 3 Lesson 7 Eq.5

7.3 CENTROID OF A QUADRANT OF A CIRCLE

Figure shows a quadrant of a circle of radius R. The differential element shown by shaded portion subtends an angle dӨ at the centre and is located at Ө with x-axis. The area of the element is approximated as the area of the triangle given by

 Module 3 Lesson 7 Fig. 7.3 Centroid of a quadrant of a circle

Fig. 7.3 Centroid of a quadrant of a circle

dA = \[{1 \over 2}\] R2 dӨ                                                                   (7.7a)

The centroidal coordinates of the differential element with reference to x and y axes are:

\[{x_{el}}\]  = \[{2 \over 3}\] R cosӨ and \[{y_{el}}\]  = \[{2 \over 3}\] R sinӨ

The first moments of the differential strip about x and y axes are computed as

                       dQx= ydA = (\[{2 \over 3}\]R sinӨ) (\[{1 \over 2}\]R2 dӨ) = ( \[{{{R^3}} \over 3}\]  sinӨ) dӨ                                         (7.7b)

                    dQy = xdA = (\[{2 \over 3}\]R cosӨ) (\[{1 \over 2}\]R2 dӨ) = ( \[{{{R^3}} \over 3}\] cosӨ) dӨ                                          (7.7c)

Therefore, the coordinates of the centroid of the quadrant of a circle are obtained by substituting Eqs. (7.7a) through (7.7c) in Eq. (7.2) and integrating between the limits of Ө from o to П/2 as follows:

Module 3 Lesson 7 Eq.6

Module 3 Lesson 7 Eq.7

7.4 CENTROID OF A SEMICIRCLE

The centroidal coordinates of a semicircle are obtained similar to the quadrant of a circle, using Eqs.(7.7a) through (7.7c) in Eq. (7.2). But the limit of integration of Ө is from 0 to П.

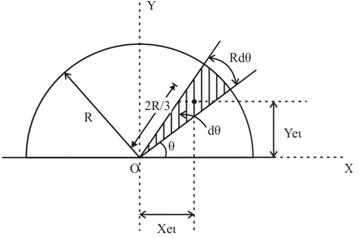
Module 3 Lesson 7 Fig.7.4 Centroid of a semicircle

 Fig.7.4 Centroid of a semicircle

Module 3 Lesson 7 Eq.8

This indicates that the centroid lies on y-axis.

 Module 3 Lesson 7 Eq.9

Module 3 Lesson 7 Eq.10

Table.1

Centroids of common shapes of areas

Module 3 Lesson 7 Table

Example: Find the position of the centroid of I-section as shown in Figure.

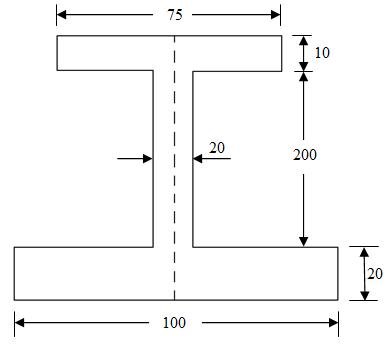
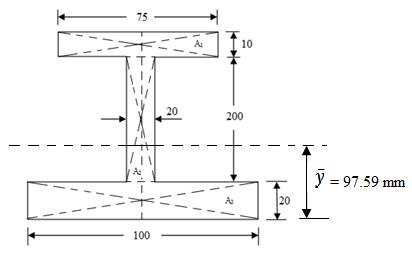
Module 3 Lesson 7 Fig.7.5(a)Module 3 Lesson 7 Fig.7.5(b)

(a)                                                                                   (b)

(all dimensions are in mm)

Fig.7.5(a) and (b)

Sol: First, divide the figure into standard areas means rectangles.

I-section is symmetrical about y-axis.

A1 = area of the top flange

A2 = area of the web

A3 = area of the bottom flange

Module 3 Lesson 7 Table 2

Example : Find the position of the centroid of the given Figure.

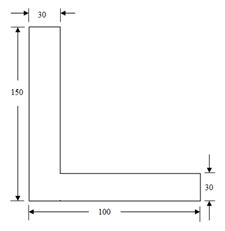
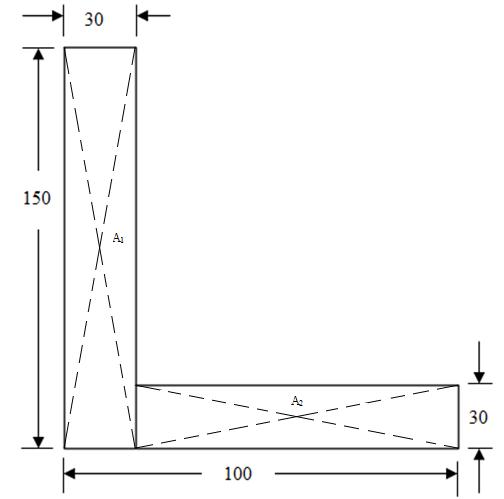
Module 3 Lesson 7 Fig.7.6(a)Module 3 Lesson 7 Fig.7.6(b)

(a)                                                          (b)

Fig.7.6

Sol:  First, divide the whole Figure into standard rectangle areas.

 Module 3 Lesson 7 Table 3

 

Example : Find the position of centroids in the following Figure.7.7(a):

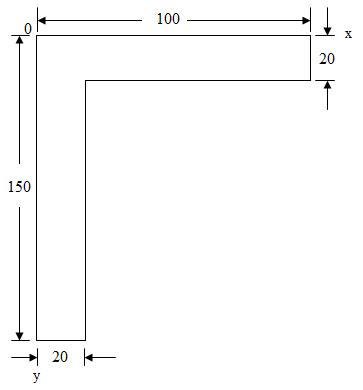
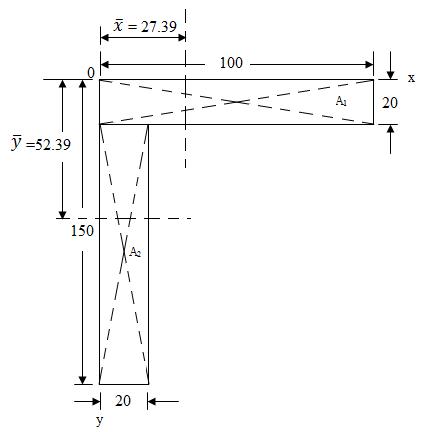
Module 3 Lesson 7 Fig.7.7(a)                         Module 3 Lesson 7 Fig.7.7(b)

   (a)                                                                                                        (b)

Fig.7.7

Sol: Divide the whole Figure into rectangular areas as shown in Figure.7.7 (b).

 Module 3 Lesson 7 Table 4

\[\bar x\] = \[{{\sum{A_i}{x_i}} \over {\sum{A_i}}}\]  = \[{{126000} \over {4600}}\]  =   27.39mm

\[\bar y\] = \[{{\sum{A_i}{y_i}} \over {\sum{A_i}}}\]  = \[{{241000} \over {4600}}\]  =   52.39mm

Last modified: Saturday, 7 September 2013, 11:31 AM