Engineering Mechanics 3(2+1)

LESSON 8. MOMENT OF INERTIA

\[{M \over I}\]   =  \[{\sigma\over y}\]          (8.1)

Where M is bending moment, I is the moment of inertia of the section about the axis of bending called neutral axis (axis at which the bending stress is zero), σ is the bending stress at any element at distance y from neutral axis. Equation (11.1) can be written as

\[\sigma\] = \[{M \over I}\] × y              (8.2)

Equation (8.2) indicates the larger the moment of inertia of an area, the smaller the bending stress, which signifies more rigidity.

Fig.8.1 Moment of Inertia

 

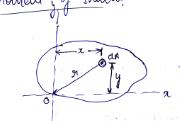
The moment of inertia of an area about x and y axes as shown in Figure 8.1 are defined by

                                                  I_x  = ∫y²dA                                                                       (8.3a)

                                                  I_y   = ∫x²dA                                                                      (8.3b)        

Where dA is the area of an element x, y stands for distance of the element from y and x axes respectively. Moment of inertia of an area is expressed as fourth power of the distance, that is cm⁴, mm⁴ or m⁴.

In case of shafts subjected to torsion or twisting moment, the moment of inertia of the cross-sectional area about its centre O is considered. This moment of inertia about 0 is called polar moment of inertia or moment of inertia about pole. It is denoted by J. The problems in which J is used are cylindrical shafts subjected to torsion, slabs subjected to rotation etc. The polar  moment of inertia is given by

                                                  J = ∫r² dA                                                                         (8.4)   

Where r is the distance of an element area from O. 

8.2 MOMENT OF INERTIA OF GEOMETRICAL FIGURES USING METHOD OF INTEGRATION

8.2.1 Rectangular Area

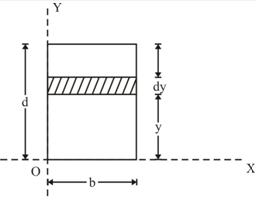
 Fig. 8.2 Moment of inertia of a rectangular area

Consider an elemental strip of width b and thickness dy in a rectangular area as shown in Fig.8.2 . Area of the element and its centroidal coordinates from x and y axes are given as

dA = b × dy

x = \[{b \over 2}\]
y = y + \[{dy \over 2}\]

Here dy/2 is very small and hence neglected. Substituting these values in Eq. (8.3a), the moment of inertia of rectangular about x-axis is determined as

I_x = ∫y² dA = ∫y² bdA

Integrating between the limits of y from 0 to d, yields

I_x =  \[\smallint\limits_0^d b{y^2}dA\] =  \[{{b{d^3}} \over 3}\]
                                                         I_x  =  \[{1 \over 3}\]  bd³                                                         (8.5)

Similarly, moment of inertia of rectangular about y-axis is

                                                         I_y =\[{1 \over 3}\]  db³                                                          (8.6)         

8.2.2 Triangular area  

Consider a triangular plane area of base width b and height d as shown in Fig.8.3. From the similar triangles ACD and AOB, the width CD of the element can be written as

 

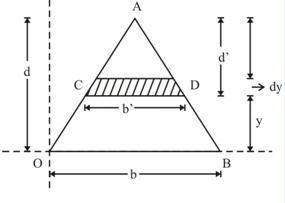
Fig.8.3  Moment of inertia of a triangle about its base

 The area of the elemental strip (shown hatched) is

dA = bꞌ × dy = \[{b \over d}\left( {d - y} \right)dy\]

The moment of inertia of the triangular area about x-axis (base of the triangle) is determined by

I_x = ∫y² dA = ∫y² \[{b \over d}\left( {d - y} \right)dy\]

Integrating between the limits of y from 0 to d, gives

I_x = \[{b \over d}\smallint \limits_0^d \left( {d - y} \right){y^2}dy\]

I_x = \[{b \over d}\left[ {{{d{y^3}} \over 3} - {{{y^4}} \over 4}} ]\]  = \[{b \over d}\left[ {{{{d^3}} \over 3} - {{{d^4}} \over 4}} ]\]

                                                        I_x =  \[{{b{d^3}} \over {12}}\]                                                                     (8.7)

8.2.3 Circular Area

Consider a circular area of radius R as shown in Fig.8.4(a) and 4(b), with an elemental area as indicated by shaded part. Fig.8.4(b) gives the enlarged view of the element ABCD.

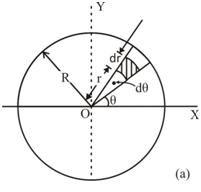
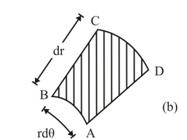
Fig.8.4 Moment of inertia of a circle

The area of the element,

dA = Area of ABCD

                     = arc length AB × BC

dA = rdӨ × dr

The centroidal coordinates of the element from x and y axes are given as

x = \[\left( {r + {{dr} \over 2}} \right)cos\left( {\theta+ {{d\theta } \over 2}}) \approx rcos\theta\]

and

y = \[\left( {r + {{dr} \over 2}} \right)sin\left( {\theta+ {{d\theta } \over 2}}) \approx rsin\theta\]

Using Eq. (8.3), the moment of inertia of circular area about x and y axes are determined as:

I_x =∫y² dA = ∫r² sin²Ө × rdӨ ×dr

I_x = ∫r³ dr × ∫sin²ӨdӨ

With the integration limits of r from 0 to R and Ө from 0 to 2П results

and                                             I_y = ∫x² dA = ∫r ² cos²Ө × rdӨ ×dr

As both x and y axes pass through the centroid of the circular area, Equations (8.8a) and (8.8b) give the moment of inertia of circle about its centroidal axes.

The above concept can be extended to obtain the moment of inertia of semicircular and quarter circular area as given below.

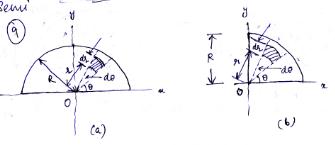
Fig.8.5 Moment of inertia of : (a) semicircle, and (b) quarter circle

Moment of inertia of semicircular area about x and y axes is

                                                           I_x  = I_y =  \[{{{R^4}} \over 8}\]                                                             (8.9)

Moment of inertia of quarter circular area about x and y axes is       

                                                         I_x  = I_y =  \[{{{R^4}} \over 16}\]                                                              (8.10)   

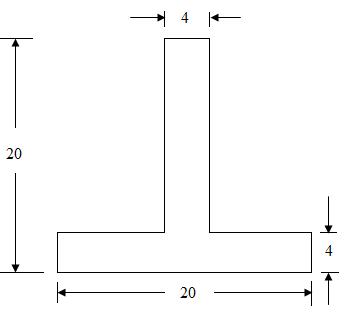
Example: A T-section is 20×20×4 as shown in Figure. Calculate the moment of inertia of the section about the x-x axis parallel to the base of T-section passing through its centroid.

 

           (a)                                                                      (b)

(all dimensions are in mm)

Fig. 8.6

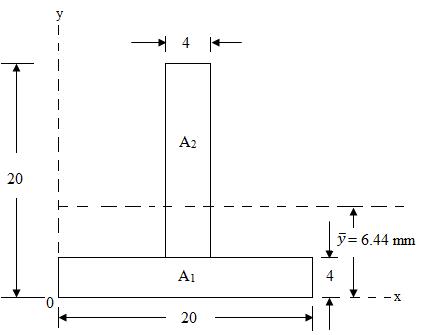
Sol: The given T-section is symmetrical about the y-y axis. Therefore, \[\bar x = {{20} \over 2}\]  = 10mm

For finding ,

\[\bar y = {{\sum {A_i}{y_i}} \over {\sum {A_i}}}\] =  \[{{928} \over {144}}\] = 6.44mm

The moment of inertia of the entire area about the centroidal x-x axis is given by

I_xx = \[[ {{{20 \times {4^3}} \over {12}} + \left( {20 \times 4}){{\left( {4.44} \right)}^2}}] + \left[ {{{4 \times {{16}^3}} \over {12}} + \left( {4 \times 16} \right){{\left( {5.56} \right)}^2}} \right]\]

=  [10667 + 1577.09] + [1365.33 + 1978.47]

= 12244.09 + 3343.8

= 15587.89 mm⁴

Example: Determine the moment of inertia about the horizontal axis passing through the centroid of the section as shown in Fig.7.

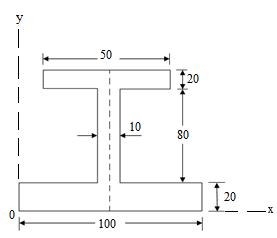
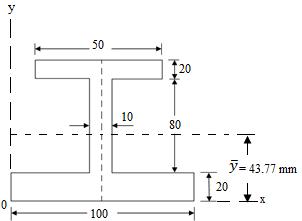
   (a)                                                                      (b)

(all dimensions are in mm)

Fig.8.7

Sol: The given I-section is symmetrical about the y-y axis, therefore,

\[\bar x = {{100} \over 2}\]  = 50 mm

To find \[\bar x\]  , we have to divide the whole Figure into standard areas.

Example: Find the moment of inertia of a plate with a circular hole about its centroidal x axis as shown in Fig.8.

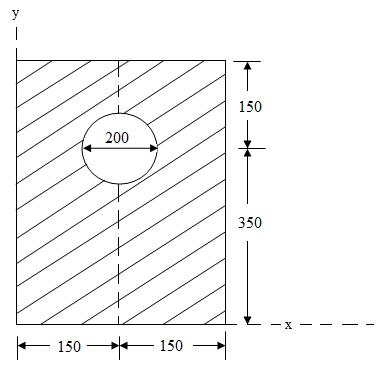
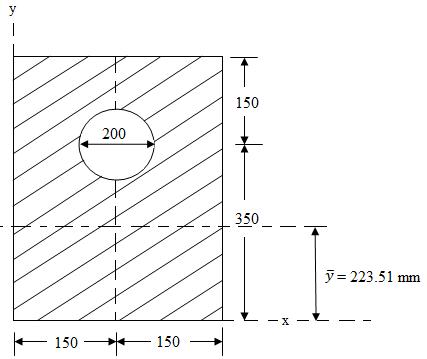
  (a)                                                                                     (b)

(all dimensions are in mm)

Fig.8.8

Sol: The given plate is symmetrical about the y-y axis, therefore \[\bar x\] = 150 mm.

To find , \[\bar y\]