Engineering Mechanics 3(2+1)

LESSON 9. Radius of Gyration of an area about an Axis

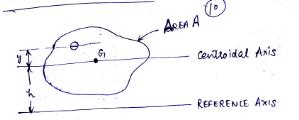
Fig.1  Parallel Axis Theorem

An axis passing through the centroid C of an area is called centroidal axis. The theorem can be proved as:

The moment of inertia of an area about a given reference axis is written using Eq.(8.3a) as

                                                       I_ref = ∫(h+y)² dA

Here                                               (h+y)² = h² + 2hy +y²

Therefore,

I_ref = ∫h² dA + ∫2hydA + ∫y²dA

I_ref = h²∫dA + 2h∫ydA + ∫y²dA

In the above expression ∫y²dA = I_cent as per Eq.(8.3a), ∫dA = A and ∫ydA = first moment of an area about centroidal axis which will be equal to zero.

Hence,                                  I_ref = h²A + I_cent

or                                          I_ref = I_cent +Ah²

 Example: The area in Fig… is symmetrical with respect to the x and y axis. The area is 150 m² and the moment of inertia with respect to the ‘b’ axis is 4200 m⁴. Determine the moment of inertia of the area with respect to the ‘a’ axis.

Solution: According to the parallel axis theorem,

I_b= I_cent +Ah²

4200 = I_cent + 150(4)²

I_cent = 2400 – 4200

I_cent = 1800 m⁴

I_a = I_cent +Ah²

= 1800 + 150(6)²

I_a = 7200 m⁴

9.2 PERPENDICULAR AXIS THEOREM

Statement: Moment of inertia of a plane area about an axis perpendicular to the plane of the figure (z-axis) is equal to the sum of moment of inertia of the same area about two rectangular axes in the plane of the area (x and y axes).

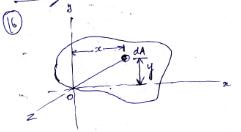
Fig.2 Perpendicular axis theorem

I_z = I_x + I_y                                                       (9.2)

According to the definition of moment of inertia [Eq.8.3a] about z-axis is given by

I_z = ∫r²dA

From Fig. 2, r² = x² + y² can be used.

Therefore,

I_z = ∫(x²+y²)dA

Iz = ∫x²dA + ∫y²dA

I_z = I_y + I_x

Or                                                              Iz = I_x + I_y

 9.3 MOMENT OF INERTIA OF GEOMETRICAL FIGURES ABOUT CENTROIDAL AXES

Using parallel Axis Theorem and moment of inertia of geometrical figures about one of their edges, the moment of inertia about their centroidal axis can be determined. Centroidal moment of inertia for a rectangle, triangle, semicircle and quarter circle are obtained as follows:

9.3.1 Rectangular Area

Moment of inertia of a rectangle about x-axis as shown in Fig.3 is given as [Eq.(8.5)]

I_x = \[{{b{d^3}} \over {12}}\]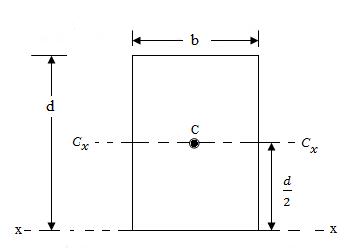

Fig.3  Moment of inertia of a rectangle about its centroidal axis

From parallel axis theorem,

I_cent = I_ref – Ah²

Ic_x = I_x – Ah² =  \[{{b{d^3}} \over 3} - bd\] \[{\left( {{d \over 2}} \right)^2}\]

                                                          I_cx =  \[{{b{d^3}} \over {12}}\]                                                                (11.12a)

Similarly

                                                          I_cx =   \[{{b{d^3}} \over {12}}\]                                                                (11.12b)