Engineering Mechanics 3(2+1)

LESSON 11. RADIUS OF GYRATION OF AN AREA ABOUT AN AXIS

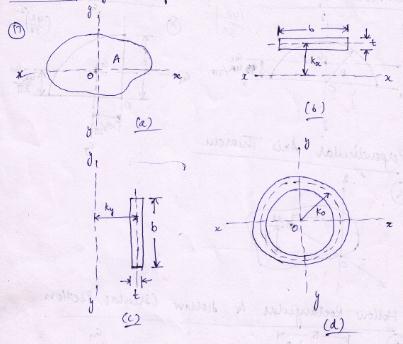
Fig.11.1 Radius of gyration

According to the parallel axis theorem, the moment of inertia of the strip about x-axis is

                                                I_xx = I_cent + AR_x²                                                        (11.19)

But I_cent = \[{{b{t^3}} \over {12}}\]  is negligible as t is small, t³ is negligibly smaller.

Therefore,

I_xx = AR_x²

Or              R_x =  \[\sqrt {{{{I_{xx}}} \over A}}\]                                  (11.20)

It is expressed in mm or cm or m.

Hence, the radius of gyration of an area about an axis is defined as the distance from the axis where thin strip (having an area equal to the given area) is to be placed so that the moment of inertia of the strip about the axis is equal to the moment of inertia of the given area about that axis.

Similar to Eq. (11.20), the radius of gyration of the area about y-axis [Figure 11.13(c)] and pole or polar radius of gyration [Figure 11.13(d)] are obtained as given in Eqs. (11.21) and (11.22).

                                                         R_y = \[\sqrt {{{{I_{yy}}} \over A}} \]                                                                (11.21)                     

R₀ = \[\sqrt {{J \over A}}\]                                                                  (11.22)

Where J = polar moment of inertia using perpendicular axis theorem

J = I_xx + I_yy

AR₀² = AR_x² + AR_y²

Hence

                                                        R₀² = R_x² + R_y²                                                          (11.23)

Example 1: Find the moment of inertia of the rectangular section as shown in Figure------- about the faces PQ and RS.

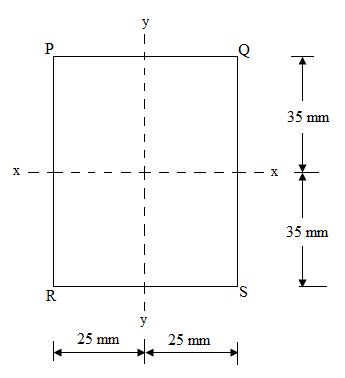
Fig.11.2

Sol: From the Figure, width b = 50 mm and depth d = 70 mm

The moment of inertia of the entire rectangular area about PQ is given by

I_PQ = I_xx + Ah²

                                                         = \[{{b{d^3}} \over {12}} + \left( {b \times d} \right){h^2}\]

                                                        = \[{{50 \times {{70}^3}} \over {12}} + \left( {50 \times 70} \right) \times {\left( {35} \right)^2}\]

                                                        =1429166.67 + 4287500

                                                       = 5716666.67 mm⁴

I_BC = I_yy + Ah²

                                                             = \[{{b{d^3}} \over {12}} + \left( {b \times d} \right){h^2}\]

                                                             = \[{{70 \times {{50}^3}} \over {12}} + \left( {70 \times 50} \right) \times {\left( {25} \right)^2}\]

                                                            = 729166.67+2187500

                                                            = 2916666.67 mm⁴

Example 2: Find the moment of inertia of a hollow rectangular section about two mutually perpendicular axes in its plane and passing through its centroid . The dimensions of the outer rectangle are 80 mm×100 mm and that of the inner rectangle is 60 mm×80 mm.

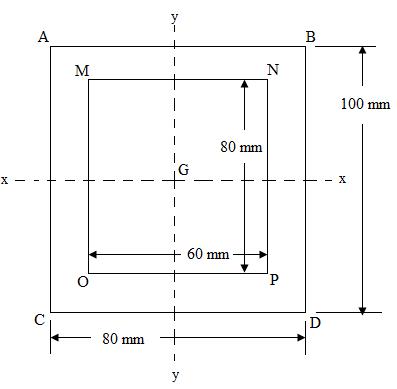
Fig.11.3

 Sol: Outer rectangle: B = 80 mm and D = 100 mm

       Inner rectangle: b = 60 mm and d = 80 mm

The formula is            I_Gx =  \[{1 \over {12}}\left( {B{D^3} - b{d^3}} \right)\]

                                           =  \[{1 \over {12}}\left( {80 \times {{100}^3} - 60 \times {{80}^3}} \right)\]

                                           = 4106666.67 mm⁴    

                                   I_Gy = \[{1 \over {12}}\left( {D{B^3} - d{b^3}} \right)\]
  

                               =  \[{1 \over {12}}\left( {100 \times {{80}^3} - 80 \times {{60}^3}} \right)\]

                               = 2826666.67 mm⁴     

Example 3: Determine the moment of inertia and radius of gyration about the horizontal axis passing through the centroid of the section as shown in Figure.

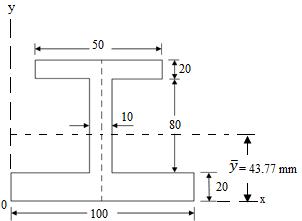
Fig.11.4

Sol: The given I-section is symmetrical about the y-y axis, therefore,

\[\bar x = {{100} \over 2}\]  = 50 mm

To find , we have to divide the whole Figure into standard areas.