Site pages
Current course
Participants
General
Module- 1 Scope and importance of food processing....
Module- 2 Processing of farm crops; cereals, pulse...
Module- 3 Processing of animal products
Module- 4 Principal of size reduction, grain shape...
Module- 5 Theory of mixing, types of mixtures for ...
Module- 6 Theory of separation, size and un sized ...
Module- 7 Theory of filtration, study of different...
Module- 8 Scope & importance of material handl...
Lession. 23 Screen Analysis
The fine particles are generally specified accordingly to their screen analysis. A screen analysis of a material is carried out by using testing sieves. A set of standard screens is arranged serially in a stack in such a way that the coarsest and finest of the screens is at the top and bottom respectively. An analysis is carried out by placing the sample on the top screen and shaking in a definite manner, either manually or mechanically, for a definite period of time. The material retained on each screen is to be removed and weighed. The amount of material retained on each screen is expressed as the weight fraction of the total sample.

As the particles retained on any one screen are passed through the screen immediately above it, two numbers are needed to specify the size, first the screen through which the fraction passes and the other on which that fraction is retained. Hence, the notation 8/10 means the material is such that it passes through the screen of mesh number 8 and collects on the screen of mesh number 10 (through 8 mesh and on 10 mesh). An analysis reported in a tabular form is called a differential analysis.
The material that is retained on the screen is the oversize and the material passes, it is the undersize. Thus, a -8 to +10 fraction means, the fraction of the material that passes through 8 mesh screen but is retained on a 10 mesh screen.
Differential Screen Analysis
|
Mesh |
Weight fraction retained |
|
6/8 |
0.017 |
|
8/10 |
0.235 |
|
10/14 |
0.298 |
|
14/20 |
0.217 |
|
20/28 |
0.105 |
|
28/35 |
0.062 |
|
35/48 |
0.028 |
|
48/65 |
0.017 |
|
65/100 |
0.010 |
|
100/150 |
0.005 |
|
150/200 |
0.002 |
|
Pan |
0.004 |
|
|
1.000 |
Other method of screen analysis is a cumulative analysis. It is obtained from the differential analysis by adding cumulatively, the individual weight fractions of material retained on each screen, starting with that retained on the largest mesh, and tabulating the cumulative sums against the screen opening of the retaining screen of the last to be added.
If we define ɸ by the equation of the form:
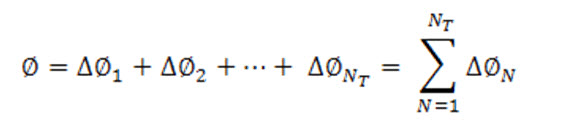
Where, ∆ ɸ1, ∆ ɸ2, ….. are the weight fractions of material retained on screens 1,2,…….. numbered serially from top of the deck.
Then the cumulative analysis is the relation between ɸ and screen opening. The quantity ɸ is the weight fraction of the sample that consists of particles larger than the screen opening. For the entire sample, the value of ɸ is unity. The cumulative analysis corresponding to the differential analysis of shown above is given hereunder.
Table 2: Cumulative screen analysis
|
Mesh |
Cumulative fraction retained (ɸ) |
|
6 |
0.000 |
|
8 |
0.017 |
|
10 |
0.252 |
|
14 |
0.550 |
|
20 |
0.767 |
|
28 |
0.872 |
|
35 |
0.934 |
|
48 |
0.962 |
|
65 |
0.979 |
|
100 |
0.989 |
|
150 |
0.994 |
|
200 |
0.996 |
|
Pan |
1.000 |
ɸ = cumulative fraction retained on screen
1-ɸ = cumulative fraction passing through screen
Fineness modulus
It is an empirical factor obtained by adding the total percentages of a sample of the aggregate retained on each of a specified series of sieves, and dividing the sum by 100. It indicates the uniformity of grind in resultant product. The fineness modulus is based on the percentages of aggregates retained on a specified series of sieves.
Sieve analysis and fineness modulus of sand (Sample size = 500.3 g)
|
Sieve size |
Cumulative mass retained (g) |
Cumulative % retained |
|
5 mm |
31.5 |
6.3 |
|
2.5 mm |
99.1 |
19.8 |
|
1.25 mm |
195.6 |
39.1 |
|
630 micron |
306.7 |
61.3 |
|
315 microns |
367.2 |
73.4 |
|
160 microns |
482.8 |
96.5 |
Cumulative percent retained = 100 (cumulative mass retained/mass of total sample)
FM = (∑Cumulative percent retained / 100)
Fineness Modulus = (6.3+19.8+39.1+61.3+73.4+96.5) / 100 = 2.964
The average particle size, Dp in mm represented in terms of fineness modulus and can be estimated by the following equation. This gives an idea about the size distribution of comminuted product.
Dp = 0.135 (1.366) FM