Soil Mechanics

LESSON 17. Permeability of Soil

Fig.17.1. Flow of water a different type of soils

 

Darcy’s Law

Velocity (v) of flow is proportional to the hydraulic gradient (i). Thus,

V = Ki              (17.1)

where k is the coefficient of permeability (cm/sec) or hydraulic conductivity. If i is equal to one, the v = k. Thus, coefficient of permeability is velocity of water for unit hydraulic gradient. Hydraulic gradient can be expressed as: i = Δh / L , where Δh is the head loss and L is the length between two points (as shown in Figure 17.2).

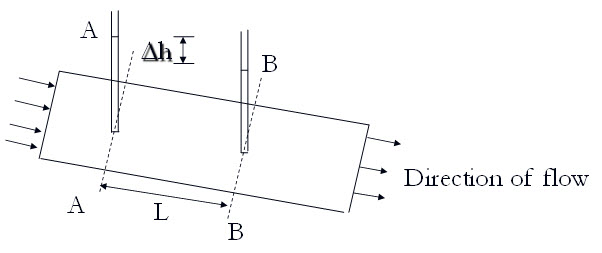
Fig.17.2. Flow of water

17.2. Permeability in layered soil

Figure 17.3 shows a layered soil system. The thickness of each layer is H₁, H₂, H₃ ………. H_n. The coefficient of permeability is k₁, k₂, k₃ …………… k_n. In case of horizontal flow, it takes place through all the layers at the same time. Thus, hydraulic gradient is same for all the layers, i.e i₁ = i₂= i₃= …… i_n = i, where n is the number of layers. However, the velocity of flow is different in different layer.

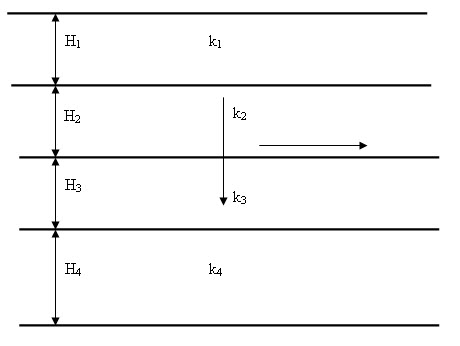
Fig. 17.3. Permeability of layered soil

According to Darcy’s law, the average discharge velocity (v_avg) can be written as:

\[{v_{avg}}={k_H}i={1 \over H}({v_1}{H_1} + {v_2}{H_2} + ............. + {v_n}{H_n})\]                           (17.2)

where k_H is the coefficient of horizontal permeability, v₁, v₂ …….v_n is the velocity of flow in different layers. H is the total thickness of the layers, i.e H₁+H₂+………+H_n = H. The Eq. (17.2) can be written as:

\[{k_H}i={1 \over H}({k_1}i{H_1} + {k_2}i{H_2} + ............. + {k_n}i{H_n})\]                                           (17.3)

\[{k_H}={1 \over H}({k_1}{H_1} + {k_2}{H_2} + ............. + {k_n}{H_n})\]                                                (17.4)

In case of vertical flow, the hydraulic gradient is different in each layer. However, the velocity of flow is same in all the layers. The total head loss is h and the head losses in each layer is h₁, h₂, ………h_n.

Head loss in each layer, \[{h_1}={H_1}{i_1}\] ,  \[{h_2}={H_2}{i_2}\].......................\[{h_n}={H_n}{i_n}\]                  (17.5)

Thus, the total head loss \[h={H_1}{i_1} + {H_2}{i_2} + .................. + {H_n}{i_n}\]                                         (17.6)

The velocity of flow is same in all the layers. Thus,

\[v={k_v}{h \over H}={k_1}{i_1}\]                                      (17.7)

where k_v is the coefficient of vertical permeability.

Thus,

\[{k_v}={{H{k_1}{i_1}} \over {{H_1}{i_1} + {H_2}{i_2} + ..........{H_n}{i_n}}}\]                              (17.8)

\[{k_v} = \frac{{H{k_1}{i_1}}}{{\frac{{{H_1}}}{{{k_1}}} + \frac{{{H_2}}}{{{k_2}}} + .......... + \frac{{{H_n}}}{{{k_n}}}}}\]             (17.9)

For more information see the Appendix 17.1

17.3. Factors affecting permeability

Some of the factors affecting permeability are:

• Grain Size

• Viscosity and temperature

• Void ratio

• Soil fabric of clay

Typical values of coefficient of permeability of various soils are presented as (Das, 1999):

Appendix 17.1    

Head loss in each layer,  \[{h_1}={H_1}{i_1}\] ,  \[{h_2}={H_2}{i_2}\]...................\[{h_n}={H_n}{i_n}\]              (17.10)

The total head loss \[h={h_1} + {h_2} + .................. + {h_n}\]                   (17.11)

The velocity of flow is same in all the layers. Thus,

\[v={k_v}{h \over H}={k_1}{{{h_1}} \over {{H_1}}}={k_2}{{{h_2}} \over {{H_2}}}=\cdots={k_i}{{{h_i}}\over {{H_i}}}=\cdots={k_n}{{{h_n}} \over {{H_n}}}\]                                                         (17.12)

where k_v is the coefficient of vertical permeability. Rearranging,

\[h=v{H \over {{k_v}}}\quad {h_1}=v{{{H_1}}\over{{k_1}}}\quad {h_2}=v{{{H_2}}\over{{k_2}}}\quad\cdots{h_i}=v{{{H_i}}\over{{k_i}}}\quad\cdots{h_n}=v{{{H_n}}\over{{k_n}}}\]                      (17.13)

The total head loss

\[h=v{H \over{{k_v}}}=v{{{H_1}}\over {{k_1}}}+v{{{H_2}}\over{{k_2}}}+\cdots v{{{H_i}}\over{{k_i}}}+\quad\cdots v{{{H_n}}\over {{k_n}}}\]                         (17.14)

\[{H \over{{k_v}}}={{{H_1}}\over{{k_1}}}+{{{H_2}}\over {{k_2}}}+\cdots{{{H_i}} \over {{k_i}}}+\quad\cdots{{{H_n}}\over {{k_n}}}\]                                       (17.15)

\[{k_v} = \frac{H}{{\frac{{{H_1}}}{{{k_1}}}+\frac{{{H_2}}}{{{k_2}}}+\cdots\frac{{{H_i}}}{{{k_i}}}+\quad\cdots\frac{{{H_n}}}{{{k_n}}}}}\]                 (17.16)

 References

Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

PPT of Professor N. Sivakugan, JCU, Australia.

 

Suggested Readings

• Ranjan, G. and Rao A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

• Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.

• Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.

• PPT of Professor N. Sivakugan, JCU, Australia (www.geoengineer.org/files/permy-Sivakugan.pps‎).

• Das, B.M. (1999). Principles of Foundation Engineering. PWS Publishing, USA.