Soil Mechanics

LESSON 18. Measurement of Permeability

Constant Head Test

Constant head test is suitable for coarse grained soil as sufficient discharge is required to determine the coefficient of permeability. Figure 18.1 shows the schematic diagram of constant head permeameter. The water is allowed to flow through the soil sample from a reservoir such a way that a constant water level is maintained in the reservoir by overflow. The quantity of water (Q) flowing through the soil for a particular time (t) or discharge is measured. The coefficient of permeability is determined as:

\[k={{QL} \over {Aht}}cm/s\]            (18.1)

where

k = coefficient of permeability (cm/s)

Q=discharge collected in time t (cm³/s)

A = c/s area of the sample (cm²)

h = head drop (distance) in manometers levels (cm)

L = distance between manometer tapping point (cm)

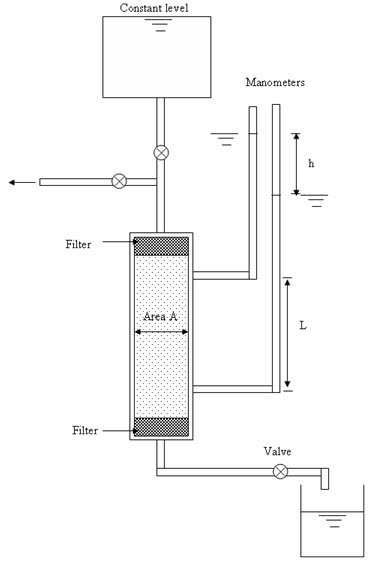
Fig.18.1. Constant head permeameter

Falling Head Test

Falling head test is suitable for fine sands, silts. Figure 18.2 shows the schematic diagram of falling head permeameter. The water is allowed to flow through the soil sample and the height difference of the water level in the stand pipe for a particular time interval is measured. The coefficient of permeability is determined as:

\[k=2.3{{aL} \over {At}}{\log _{10}}{{{h_1}} \over {{h_2}}}\]                (18.2)

where

k = coefficient of permeability (cm/s)

A = c/s area of the sample (cm²)

a= area of the stand pipe (cm²)

h = distance in manometers levels (cm)

h₁ (cm) and h₂ (cm) = height of the water level in stand pipe in time difference t (s)

Unconfined Pumping Tests

Figure 18.3 shows the unconfined pumping test procedure. Here aquifer is underlain by an impermeable layer and pumping well is extended up to the bottom of the permeable layer as shown in Figure 18.3. Two observation wells are inserted in the aquifer. The permeability is determined as:

\[k=2.3{q \over \pi }{{{{\log }_{10}}({r_2}/{r_1})} \over {(h_2^2 - h_1^{2)}}}\]                       (18.3)

where q is discharge, k is coefficient of permeability, h₁ and h₂ can be determined by measuring the drawdown at the observation wells (as shown in the Figure 18.3).  r₂ and r₁ are the distance of the observation well from the pumping well.

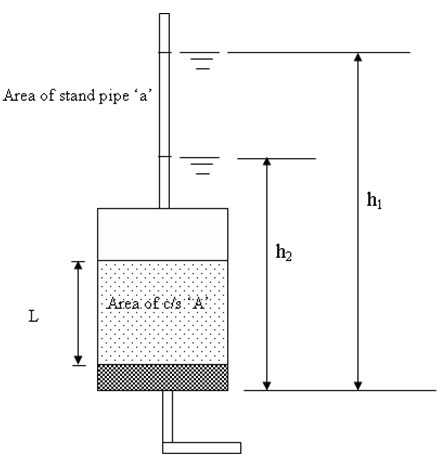
Fig. 18.2. Falling head permeameter

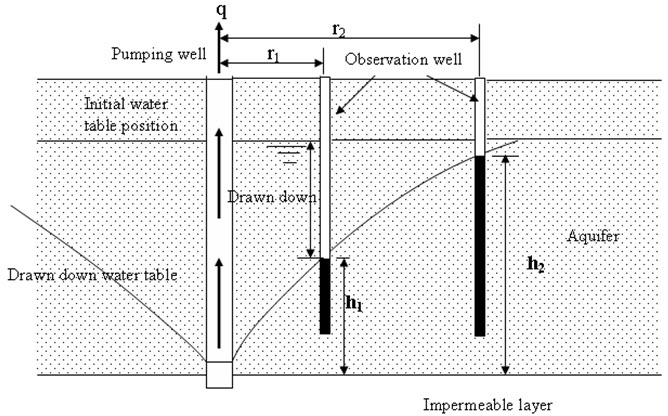
Fig. 18.3. Pumping test in unconfined aquifer

Confined Pumping Tests

Figure 18.4 shows the confined pumping test procedure. Here aquifer is confined in top and bottom by impermeable layers as shown in Figure 18.4. Two observation wells are inserted in the aquifer. The permeability is determined as:

\[k=2.3{q \over {2\pi D}}{{{{\log }_{10}}({r_2}/{r_1})} \over {(h_2^{} - h_1^{})}}\]            (18.4)

where q is discharge, k is coefficient of permeability, h₁ and h₂ can be determined by measuring the drawdown at the observation wells (as shown in the Figure 18.3).  r₂ and r₁ are the distance of the observation well from the pumping well. D is the thickness of the aquifer.

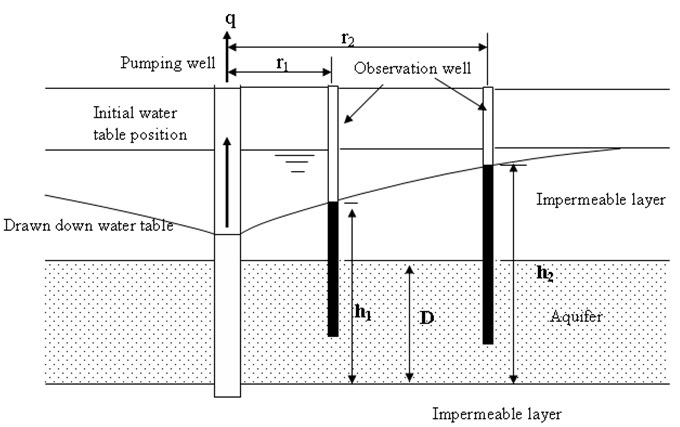
Fig. 18.4. Pumping test in confined aquifer

 

References

Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India

PPT of Professor N. Sivakugan, JCU, Australia.

 

Suggested Readings

Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.

Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.

PPT of Professor N. Sivakugan, JCU, Australia (www.geoengineer.org/files/permy-Sivakugan.pps‎).