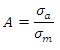Machine Design 3(2+1)

LESSON 6. DESIGN FOR DYNAMIC LOADING - I

6.2 Types of Cyclic Stress

A number of different regular and irregular patterns are followed by cyclic stresses in machinery but generally it follows sinusoidal pattern because of the nature of some rotating machinery. Also for design purpose, only maximum and minimum value of stress is important and not the wave form. Therefore, sine wave can be conveniently used to represent any kind of variation of stress between the minimum and maximum values of stress. Following are some important types of cyclic stresses depending upon the level of minimum and maximum stress between which the stress fluctuates:

Completely Reversed Stress	extreme values of stress are of equal magnitude and opposite nature with mean equal to zero	Refer      Figure 6.1 a
Repeated  Stress	stress varies from zero to certain maximum value (nature of stress does not change)	Refer  Figure 6.1 b
Fluctuating Stress	minimum value and maximum value of stress is of same nature (tensile or compressive)	Refer  Figure 6.1 c
Alternating Stress	stress changes its nature and magnitude of extreme values of tensile and compressive stress is not same

 

All variable stresses can be considered to be made of two components – static component called mean stress (s_m) and a variable component called stress amplitude (s_a).

Mean Stress =			Stress Amplitude =
Stress Range,
Stress Ratio,			Amplitude Ratio,

                         

Figure 7.1 a. Completely Reversed Stress                   Figure 7.1 b. Repeated Stress

 

Figure 7.1 c. Fluctuating Stress

6.3 Fatigue Curve (S-N Curve) & Endurance Limit

Fatigue properties of the materials are obtained with the help of standard rotating beam test, in which a highly polished circular section specimen, shown in figure 6.2, is subjected to cyclic loads. Specimen subjected to constant bending moment is rotated at a very high speed due to which fibers of the specimen (except those on neutral axis) undergo repeated stress reversals (maximum tensile stress to maximum compressive stress). Stress-time plot is shown in figure 6.3. Test is repeated for a number of similar specimens, subjecting them to different values of stress and number of stress reversals that the specimen survives before fracture are counted. First test is performed by subjecting the specimen to stress, below ultimate tensile strength and subsequent tests are performed at decreased levels of stress.

                          

Figure 7.2 Completely Reversed Stress                                            Figure 7.3 Stress-time Plot

Results of the tests are plotted between stress (S) and number of cycles (N), generally on a log-log scale. S-N Curve is shown in figure 6.4.

 Figure 7.4 S-N Curve

The ordinate of the S-N curve is called Fatigue Strength (S_f), which can be defined as the maximum stress that the material can withstand for a specified number of stress reversals. For ferrous metals and their alloys, S-N curve becomes horizontal after 10⁶ to 10⁷ cycles, which means that the material can survive infinite number of stress reversals, if the induced stress is below this level.  Stress corresponding to this horizontal line is called endurance limit or fatigue limit.

Fatigue or Endurance Limit (S'_e) can be defined as maximum amplitude of completely reversed stress that the standard specimen can sustain for an unlimited number of cycles without fatigue failure. Study of fatigue in which failure takes place before 1000 cycles is called Low Cycle Fatigue. High Cycle Fatigue is concerned with failure corresponding to stress cycles greater than 1000 cycles.

In the absence of experimental fatigue data, following relations are sometimes used:

For Steel, S'_e = 0.5 S_ut

For Cast Iron, S'_e =  0.4 S_ut

6.4 Endurance Limit Modifying Factors

Rotating-beam specimen used to determine endurance limits is very carefully prepared and is tested under closely controlled conditions. The endurance limit of any machine element cannot match the values obtained from test due to variation in material, quality of manufacture, environmental conditions and design. Therefore, the endurance limit obtained by the test is modified using some factors to obtain more reasonable results. Endurance Limit of a particular machine part can then be estimated using following relation:

Where, _{\[S_e^{'}\]}    = Endurance Limit of the specimen

K_surf       = Surface Finish Factor

K_size      = Size Factor

K_load     = Load Factor

K_rel    = Reliability Factor

K_temp  = Temperature Factor

K_f      = Fatigue Stress Concentration Factor

6.4.1 Surface Finish Factor (K_surf)

Surface of the rotating beam specimen is highly polished but most of the machine members don’t have that kind of surface finish requiring a modification in the endurance limit obtained by rotating beam experiment. Surface finish factor depends upon the manufacturing process used and ultimate tensile strength of the material. Its value can be selected with the help of chart shown in figure 6.5.

Figure 7.5 Surface Finish Factor

6.4.2 Size Factor (K_size)

Standard rotating beam specimen has a diameter of 7.6 mm and modification factor, K_size must be applied for machine elements of different sizes. Its value may be taken as:

Size Factor, Ksize	1.0	0.85	0.75
Diameter (d) of Machine Element (mm)	d ≤ 7.6 mm	7.6 ≤ d ≥ 50 mm	d ≥ 50 mm

 

6.4.3 Load Factor (K_load)

In rotating beam test, specimen is subjected to bending load and completely reversed stress cycles but many machine members are subjected to different types of loads and stress cycles. To account for this, endurance limit is modified using load factor, K_load  and its value can be taken as:

Load Factor, Kload	1.0	0.85	0.59
Type of Completely Reversed Load	bending	tensile	torsional

6.4.4 Reliability Factor (K_rel)

Endurance limit obtained experimentally is the mean value and it varies even for same material and conditions. Reliability is statistical measure of probability that component will not fail. Reliability factor to modify endurance limit can be taken as:

Reliability (%)	50	90	95	99	99.9	99.99	99.999
Reliability Factor, Krel	1.000	0.897	0.868	0.814	0.753	0.702	0.659

 

6.4.5 Temperature Factor (K_temp)

Incease in temperature accelerates the effect of fatigue. Therefore Temperature factor, K_temp is used to modify the experimentally obtained endurance limit. It can be taken as:

            K_temp     = 1.0 for temperature ≤ 300ºC

                         = 0.5 for temperature > 300ºC

 

6.4.6 Fatigue Stress Concentration Factor (K_f)

To account for the effect of stress concentration in case of cyclic loading, endurance limit is modified by dividing it with the fatigue stress concentration factor, which is given by,

Value of this factor is less than the value of theoretical stress concentration factor, K_t, since all the materials are not equally sensitive to the notches. K_f gives the reduced value of stress concentration factor for less sensitive materials. For these materials, the effective maximum stress in fatigue is, \[{\sigma _{max}}={K_f}{\sigma _0}\]

Notch sensitivity is defined as the ratio of actual stress over nominal to the increase in theoretical stress value over the nominal stress. It is given by,

Value of K_f is always greater than one and endurance limit of standard specimen is divided by it, unlike all the other modification factors. For q = 0, K_f =1 and for q=1, K_f = K_t. q can be estimated form figure 6.6, which is based on the experimental data.

Figure 7.6 Notch Sensitivity

 

References

1. Mechanical Engineering Design by J.E. Shigley

2. Analysis and Design of Machine Elements by V.K. Jadon

3. Design of Machine Elements by VB Bhandari

4. Design of Machine Elements by M. F. Spotts

5. Design of Machine Elements by C.S. Sharma & K. Purohit

6. Machine Elements in Mechanical Design by Robert L. Mott