Ground Water,Wells and Pumps 3(2+1)

Lesson 13 Overview of Field Pumping Test

Pumping test (sometimes also called field pumping test) can be defined as a field investigation in which a well is pumped in a specific fashion and the resulting drawdowns are measured in the pumping well itself and/or observation wells installed at different locations over the groundwater basin under investigation. Many modern books on groundwater/hydrogeology mostly use the terminology ‘Aquifer test’ instead of the widely-used terminology ‘Pumping test’. Although the use of both the terms is recommended, the ‘aquifer test’ is a broader term which encompasses non-conventional tests also. Note that the phrases ‘pumping test’ and ‘pump test’ convey completely different meanings, and hence they should be used cautiously!

13.2 Purpose of Pumping Test

The pumping test or aquifer test is the only standard method available to date for determining the hydraulic characteristics of various aquifer systems [e.g., T, K, S or S_y, leakage factor (B) and hydraulic resistance (C)] and those of production wells (e.g., well parameters, safe well yield, etc.). Long-term time-drawdown pumping tests can also provide information about the presence of subsurface hydraulic barriers, if any, as well as the existence of a boundary and its type (recharge, impermeable or leaky boundary). Properly placed observation wells at different locations and in different directions can provide information about the degree of heterogeneity and anisotropy of aquifer systems. Further, step-drawdown tests can provide important information about the hydraulic characteristics of production wells (i.e., aquifer loss coefficient, well loss coefficient, well efficiency, well specific capacity, and safe well yield) and the condition of production wells.

 

13.3 Types of Pumping Tests

There are primarily four types of pumping tests/aquifer tests. They are as follows:

(1) Time-Drawdown Test:

(a)    Interference Test

(b)    Distance-Drawdown Test

(c)     Single Well Test

(2) Recovery Test

(3) Step-Drawdown Test or Variable Rate Test

(4) Injection Tests:

(a) Time-Groundwater Level Rise Test

(b) Step-Injection Test

 

Aquifer tests (1) and (2) are mainly used for determining various hydraulic parameters of different aquifer systems (viz., confined, leaky confined and unconfined aquifers). However, the step-drawdown test is used for determining the hydraulic characteristics of production wells and for evaluating the condition of existing production wells.

 

Instead of a production well, if an injection well is used to conduct a pumping test, it is called an injection test. The injection test can be designed to observe ‘time-groundwater level rise’ in an injection well itself or in nearby observation wells. In addition, the injection test can be designed to conduct a ‘step-groundwater level rise’ or ‘step-injection’ test. Since in injection tests, water is injected into a production well instead of pumping, it is not technically sound to call it a pumping test; aquifer test is a better terminology to assimilate this type of test. Thus, the term ‘aquifer test’ includes both pumping tests and injection tests.

 

When aquifer tests 1(a, b, c), (2), and 4(a) are conducted until an equilibrium (steady-state) or quasi-equilibrium (quasi steady-state) condition is reached, they are called steady-state tests. On the other hand, when these tests are conducted for a relatively short period and are completed before the steady-state or quasi steady-state condition is reached, they are called unsteady-state tests or transient tests.        

 

The type of pumping test/aquifer test performed depends on the purpose, available resources (labor, money, instruments/equipment, etc.) and time, and site-specific limitations. Site-specific limitations, for instance, could be limited water disposal facilities, water quality constraints, or noise restrictions.

13.4 Tests for Determining Hydraulic Parameters of Aquifers

13.4.1 Steady and Unsteady Time-Drawdown Tests

Time-drawdown pumping tests are suitable for the determination of aquifer parameters. Based on the type of data yielded by time-drawdown pumping tests, these tests fall into two categories: (a) unsteady-state tests or transient tests, and (b) steady-state tests or equilibrium tests. In both the categories, the pumping rate is kept constant throughout the duration of the test. In unsteady-state tests, groundwater level changes in response to a constant pumping rate are measured over a period of time. The data obtained from transient tests are useful for determining almost all the hydraulic parameters of aquifer systems.

 

In steady-state tests, pumping is continued until near-equilibrium conditions are reached (i.e., there are negligible changes in groundwater levels with time). In practice, steady-state tests approach only quasi-steady-state conditions in most aquifer systems. This is because true equilibrium may never be obtained under field conditions because of ever-present aquifer recharge or discharge in a groundwater system. The data obtained from steady-state tests can be used to calculate only aquifer transmissivity or hydraulic conductivity and, in some cases, leakance (leakage coefficient); storage coefficient of an aquifer system cannot be determined from these data.

 

While conducting time-drawdown tests, drawdown can be measured either in one or more observations wells (called ‘interference test’) or in the pumping well itself (called ‘single well test’).  They are described below.

 

13.4.1.1 Interference Test

The measurement of groundwater level changes (drawdowns) in response to pumping in one or more observation wells is known as an interference measurement as shown in Fig. 13.1. Depending upon the nature of the interference test, it can be steady-state test and/or unsteady-state test. Unlike pumping well measurements, interference measurements contain no turbulent flow components, and hence the drawdown measured in observation wells is the representative of that in aquifers. This is the reason that interference-test data are preferred for determining aquifer parameters. For interference tests, it is essential that the observation wells should be completed in the same aquifer as the pumping well.

 

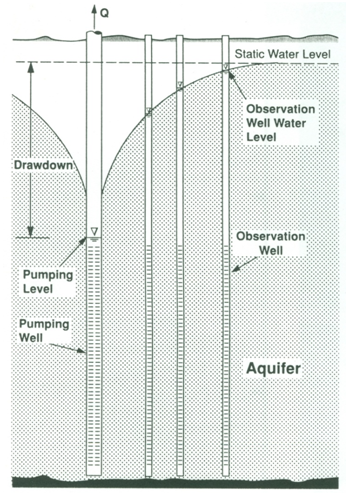
Fig. 13.1. Illustration of an interference pumping test.

(Source: Roscoe Moss Company, 1990)

 

Determination of aquifer transmissivity (T) or hydraulic conductivity (K) from the steady-state test data usually requires the steady drawdown data from two observation wells or the steady drawdown data from at least one observation well in addition to the pumping well; the drawdown measured in a pumping well needs to be corrected for well losses. However, the steady drawdown data from one observation well or pumping well can also be used for computing K or T, if the radius of influence is known. On the other hand, the determination of aquifer parameters including the storativity (storage coefficient) requires transient drawdown data from one observation well only.

 

As a rule, the more observation wells available for measurement during a time-drawdown test, the more reliable the information obtained on aquifer characteristics. Since real-world aquifer systems exhibit significant heterogeneity, it is essential that the time-drawdown measurements during a pumping test should be done at as many locations as possible and that time-drawdown tests should be conducted at various sites over a basin or sub-basin so as to account for the aquifer heterogeneity. If the observation wells are oriented in different directions away from the pumping well, aquifer anisotropy can also be determined.

 

13.4.1.2 Distance-Drawdown Test

In distance-drawdown tests, drawdown is measured in three or more observation wells located at different radial distances from a pumping well, and thereby a set of distance-drawdown data is obtained. This test as such is not conducted separately in the field; rather one can create such dataset from the time-drawdown measurements at different locations during a time-drawdown test. Thus, depending on the nature of time-drawdown tests, the distance-drawdown data can be of two types: distance-steady drawdown data or distance-unsteady drawdown data; the former dataset can yield only aquifer transmissivity (T) or hydraulic conductivity (K), whereas the latter dataset can yield both T and storage coefficient (S). The distance-drawdown data are useful for cross-checking the aquifer parameters obtained from time-drawdown data. In addition, the distance-drawdown data can be used to calculate ‘radius of influence’ (R₀) and ‘well loss’ (and hence ‘well efficiency’).

  

13.4.1.3 Single Well Test

If the time-drawdown aquifer test is conducted in such a way that the drawdown is measured only in a pumping/production well itself, it is known as a single well test. Single well test is normally conducted when there are no observation wells in a basin or sub-basin and it is not possible to install observation wells due to money and/or time constraints. Hence, single well tests are less expensive than the interference tests.

 

It should be noted that the drawdown in a pumping well consists of two types of head losses: (a) aquifer loss or formation loss (drawdown due to laminar flow in the aquifer which is known as ‘theoretical drawdown’), and (b) well loss (drawdown due to turbulent flow in the immediate vicinity of the pumping well through the screen and/or gravel pack as well as due to flow inside the well to the pump intake) as shown in Fig. 13.2. Since the well loss is associated with turbulent flow, it is proportional to an n^th power of the pumping rate (well discharge) where n is a constant greater than one. Thus, the total drawdown in a pumping well or well drawdown (s_w) is given as (Fig. 13.2):

 

s_w = Aquifer Loss + Well Loss                                                  (13.1)

 

Or,                                                              s_w= BQ + CQⁿ                                                                                                      (13.2)         

Where, B = aquifer/formation loss coefficient, Q = pumping rate (well discharge), and C = well loss coefficient which is a function of the radius, construction and condition of the pumping well.

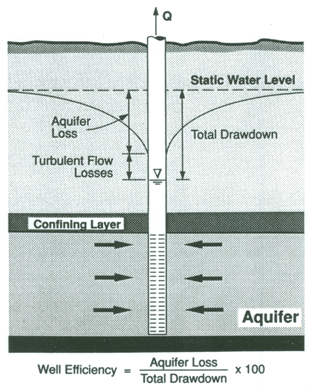
Fig. 13.2. Components of drawdown in a pumping well.

(Source: Roscoe Moss Company, 1990)

 

It is obvious from Eqn. (13.2) that the aquifer loss increases linearly with increasing pumping rate, while the well loss increases non-linearly with increasing pumping rate. Therefore, the well loss can be a sizeable component of the well drawdown (i.e., total drawdown) when pumping rates are large. The first term (aquifer loss) on the right hand side of Eqn. (13.2) can be calculated by using Thiem equation (if the well drawdown is steady) or Theis equation (if the well drawdown is unsteady). However, the second term (well loss) can be determined by step-drawdown test (described later in this lesson) or can be estimated from distance-drawdown data. Well losses can be minimized by proper design and development of pumping wells. However, clogging or deterioration of well screens can increase well losses in old pumping wells.

 

Thus, the drawdown measured in pumping wells is not the representative of that in the aquifer. Consequently, single well test is generally avoided unless the value of well loss for a particular pumping well is known so that the measured well drawdowns could be corrected to be representative of aquifer drawdowns. Note that the time-drawdown data obtained from single well tests should be used for the determination of T or K only, because these data do not yield reliable estimates of S.    

 

13.4.2 Recovery Test

Recovery test is conducted at the end of a time-drawdown aquifer test. It is an unnsteady-state aquifer test in which groundwater rise is measured with time in a pumping/production well or in an observation well after pumping has been stopped (Fig. 13.3). It is apparent from Fig. 13.3 that if the pumping of a well is stopped, the groundwater level in the aquifer gradually starts increasing and it should theoretically return to its pre-pumping groundwater level; this time period is known as recovery period or recovery phase. From the water-level data measured during recovery period, ‘residual drawdown’ (difference between the pre-pumping groundwater level and the depth to groundwater after the pump is stopped) or ‘recovery’ (difference between the extrapolated time-drawdown curve and the residual drawdown) is computed at different times during recovery period (Fig. 13.3). The ‘time-residual drawdown’ data or the ‘time-recovery’ data thus obtained are used for determining aquifer parameters.

 

In general, the data obtained during the recovery period are more reliable than during the pumping period due to the lack of water-level fluctuations caused by discharge variations and the absence of turbulence. Like the time-drawdown data from single well tests, the time-recovery data measured in pumping wells can yield only T or K. However, if the time-recovery data are measured in observation wells, both T and S can be determined.

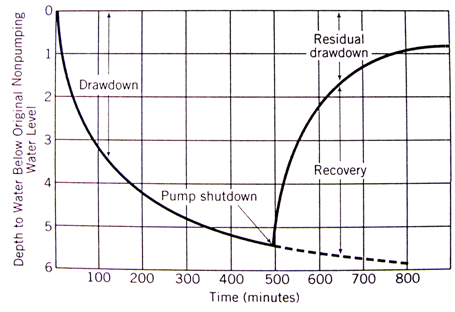
Fig. 13.3. Illustration of time-drawdown and recovery tests.

(Source: Schwartz and Zhang, 2003)

 

Since additional expenses are not required for conducting a recovery test, it is always recommended to carry out this test during an aquifer-test program for a basin or sub-basin. The recovery test provides an independent and additional estimate of aquifer parameters, which can be compared with the aquifer parameters obtained from time-drawdown data to gain confidence in the analysis.

 

13.4.3 Injection Tests

In the area where artificial recharge projects using the well injection technique are running, injection tests can be conducted in that area. The test procedures and the equations used for analyzing injection well test data are similar to those of drawdown tests, except that the injection pressure head (i.e., difference between the static groundwater level and the groundwater level during injection) is substituted for drawdown, and the injection rate for pumping rate (Roscoe Moss Company, 1990). Thus, the data of time-groundwater level rise test can be used for determining hydraulic parameters of aquifer systems. Similarly, the data of step injection test can be used for determining the hydraulic characteristics of production wells.

 

13.5 Test for Determining Well Hydraulic Characteristics

13.5.1 Step-Drawdown Test

In a step-drawdown test (or variable rate test), changes in the drawdown of a pumping/production well are measured corresponding to the changes in pumping rate (i.e., well discharge) as illustrated in Fig. 13.4. This test is normally conducted by pumping a production well at successively greater pumping rates (i.e., Q₁ < Q₂ < Q₃ < Q₄ < Q₅) for 5 to 8 steps (pumping rates). The entire test is done in one day. Generally, the drawdown for a particular step (pumping rate) is measured until a steady-state or quasi-steady-state condition is reached. Alternatively, this test can also be conducted by pumping a production well for about 1-2 hours at each successively greater pumping rate and observing unsteady drawdown at the end of each step (i.e., after 1-2 hours of pumping). However, the analysis of ‘discharge-unsteady drawdown’ data becomes somewhat complicated. Thus, a set of ‘discharge-drawdown’ data for a particular pumping well is obtained from a step-drawdown test.

 

The ‘discharge-drawdown’ data obtained from a step-drawdown test are analyzed to determine the hydraulic characteristics of a production well such as

 

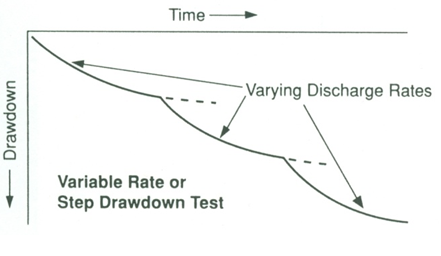
Fig. 13.4. Illustration of a step-drawdown test.

(Source: Roscoe Moss Company, 1990)

 

safe well yield, aquifer loss and well loss coefficients, specific capacity of the well (ratio of the well discharge to the corresponding drawdown), well efficiency (ratio of the theoretical drawdown to the observed well drawdown as shown in Fig. 13.2), and the relationships between drawdown and discharge, between well efficiency or specific capacity and discharge as well as the evaluation of the condition of existing production wells. Thus, the step-drawdown tests are of great significance for the design and monitoring of pumping plants as well as for estimating site-specific safe aquifer yields over a basin or sub-basin.

 

13.5.2 Critical Pumpage and Safe Well Yield

Based on the step-drawdown test data, a safe pumping rate or safe well yield for a production well can be determined. The safe well yield is generally defined as the highest pumping rate at which equilibrium conditions can be maintained in the aquifer system (Roscoe Moss Company, 1990). When the equilibrium rate is exceeded, the pumping level continues to decline at a rate proportional to the well and aquifer parameters. When this decline is quite rapid (e.g., several centimeters per minute), the well may dewater in a relatively short time period, with the pump ‘breaking suction’; the latter condition is very serious and could result in the collapse of well casing.

 

The pumping rate (well discharge) at which a rapid decline in groundwater level occurs is known as critical pumpage or critical discharge (Roscoe Moss Company, 1990). This condition varies widely from one area to another as well as from one well to another in an area. For example, in the areas having high-yielding aquifers (i.e., high values of T and S), the full capacity of a pump may not be able to create a critical pumpage situation. However, in the areas having low-yielding aquifers (i.e., low values of T and S), a rapid dewatering of the well may be achieved quite easily. Besides these factors, water quality (e.g., saltwater intrusion or contaminated water migration) also limit the safe pumping rate. This situation necessitates reduced pumping rate below the potential of production wells. Note that the safe pumping rate or safe well yield should always be less than the critical pumpage in order to ensure sustainable groundwater utilization in a basin. 

 

13.6 Design of Pumping Test

 Proper planning and design of a pumping test is essential for ensuring good-quality pumping-test data. Besides the adequate knowledge of the local lithology and types of aquifers, a proper selection of production wells to be pumped and the observations wells for drawdown measurement is also necessary. The latter requires the field information such as depth, design and condition of pumping wells; availability of water disposal facility; and the number of observation wells and their depth, design and location. On top of it, some additional decisions are to be made prior to the execution of pumping tests. These points are described in this section.    

 

13.6.1 Placement of Observation Wells and Number of Tests

Ideally, observation wells should be placed in four quadrants surrounding the production well at radial distances ranging from 3 m to 300 m (Roscoe Moss Company, 1990). Spacing between the observation wells should be closer near to the pumping well where drawdown changes are the greatest. Observation wells should be placed considering both the duration of a pumping test and aquifer parameters, because the shape of the cone of depression depends upon these two major factors. For instance, the cones of depression in the aquifers having low transmissivity are steep and limited compared to the broad and flat cones of depression in the aquifers having high transmissivity (Fig. 13.5). Similarly, if the duration of a pumping test is longer, the cone of depression is expected to extend up to a larger distance from the pumping well in comparison with the short-duration pumping test. 

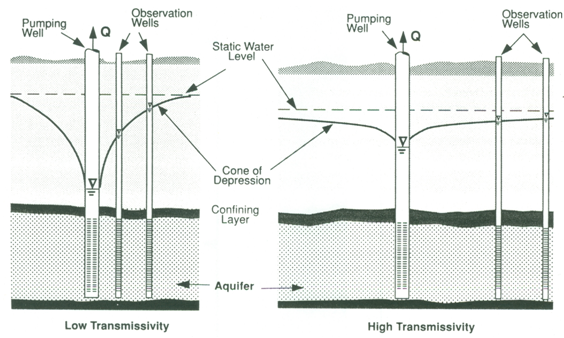
Fig. 13.5. Placement of observation wells for a pumping test.

(Source: Roscoe Moss Company, 1990)

 

Moreover, proper knowledge of the aquifer type is also important for the placement of observation wells. For example, groundwater level changes in unconfined aquifers may be measurable within only relatively short distances from the pumping well (e.g., 30 to 150 m), whereas confined aquifers may show significant changes in groundwater level hundreds (100 to 250 or more) to thousands of meters away from the pumping well (Roscoe Moss Company, 1990). Furthermore, if hydrogeologic boundaries are known or anticipated, it is desirable to place observation wells between the boundary and the pumping well. In most cases, placing observation wells at about 10 to 100 m from the center of the pumping well provides good results. The observation wells should be placed in the same aquifer in which the pumping well is installed. Also, both the pumping well and the observation well should fully penetrate the aquifer under investigation so as to avoid the complexity in the analysis of pumping-test data.   

 

As far as the number of pumping tests (or aquifer tests) and the number of observation wells are concerned, they depend on the amount of information desired, degree of precision expected, heterogeneity/anisotropy of the aquifer, and the availability of fund and time for investigation. In general, the number should be as many as techno-economically feasible for a better understanding of the spatial variation in aquifer parameters over a basin.

 

13.6.2 Pumping Rate and Test Duration

The rate of pumping during aquifer tests should be such that an appreciable drawdown occurs in most of the observation wells placed at different radial distances. It should also be ensured that the drawdowns measured during an aquifer test are not affected by any other factors. If any external factor affects the drawdown measured in a given observation well, the data become erroneous (noisy) and such data are usually not considered for analysis.  

 

As to the duration of aquifer tests, it depends on both the test purpose and the hydraulic properties of the aquifer. Since the hydraulic properties of an aquifer are to be determined by aquifer tests, they are not known prior to conducting aquifer tests. Therefore, the duration of aquifer tests mainly depends on whether one wishes to conduct unsteady-state tests or steady-state tests. The duration of unsteady-state tests is shorter (a few hours only) than that of steady-state tests which can vary from several hours to days. Essentially, the duration of an aquifer test should ensure that sufficient number of drawdown data with significant differences from one another is obtained so that the data are well spread in the graph to be plotted during analysis. Under average conditions, a leaky aquifer should be pumped for 15 to 20 hours, a confined aquifer should be pumped for 1 day, and an unconfined aquifer for 3 days or more in order to achieve steady-state (equilibrium) flow condition (Roscoe Moss Company, 1990). As such, there exist no hard and fast universal guidelines for deciding the duration of aquifer tests. However, the guidelines suggested in Table 13.1 can be followed to ensure that the aquifer-test duration exceeds the minimum pumping time mentioned in this table.

 

Table 13.1. Guidelines for deciding the duration of aquifer tests

(Source: Todd, 1980)

Sl. No.	Predominant Aquifer Material	Minimum Pumping Time
1	Silt and Clay	170 hours
2	Fine Sand	30 hours
3	Medium Sand and Coarser Materials	4 hours

 

13.6.3 Measurement of Pumping Rate and Groundwater Level

The essential measurements taken during any aquifer test are time, pumping rate (well discharge), and depth to groundwater level (i.e., drawdown or groundwater rise). Measurements of the time of start, stop and pumping interval must be made with a reasonable accuracy (±0.1 min). The pumping rate or well discharge should preferably be kept constant throughout the aquifer test. During an aquifer test, well discharge is measured at regular intervals and an adjustment is made to keep it constant. If the well discharge is small, it can be accurately measured by the volumetric method. However, if the well discharge is large, a water meter or an orifice meter installed in the delivery pipe of the pump, or a 90º V-notch (fitted with a conveyance channel wherein pumped water is diverted for disposal) can be used. The depth to groundwater level can be measured either manually using a water-level indicator and/or automatically by a water-level recorder (‘clock and chart type water-level recorder’ or ‘water-level sensor’).      

 

13.6.4 Schedule of Data Collection

Once an aquifer test is initiated, the groundwater levels in a pumping well or an observation well decline (after start of pumping) or recover (after stop of pumping) very rapidly during first one or two hours. Therefore, initially groundwater level is measured at short time intervals and thereafter the time interval is gradually increased as the pumping proceeds. The data-collection schedule presented in Table 13.2 should be followed for measuring groundwater levels in pumping wells and/or nearby observation wells during an aquifer test. Frequency of measurement is less important for the observation wells located at larger distances from the pumping well.

 

Table 13.2. Frequency of groundwater-level measurement during aquifer tests (Source: Roscoe Moss Company, 1990)

Time Since Pumping Started or Stopped	Time Interval
0-5 min	1 min
5-60 min	5 min
60-120 min (i.e., 1-2 hours)	15 min
2-6 hours	1 hour
6 hours - End of Test	2 hours

 

13.7 Response of Bounded Aquifers to Pumping

The general theory of groundwater hydraulics assumes that the aquifer is infinite in areal extent. In reality, however, aquifers are not infinite because they can be cut by tight faults (e.g., fault barriers) or they can end abruptly due to changes in geology (e.g., limited aquifer conditions or impermeable bedrock) These impermeable boundaries of an aquifer system effectively halt the spread of the cone of depression and significantly affect the pattern of drawdown in the vicinity of pumping wells (Todd, 1980; Fetter, 1994; Schwartz and Zhang, 2003). Similarly, if an aquifer system is bounded by a surface-water body (e.g., a fully penetrating stream, lake, or reservoir) or an adjacent segment of aquifer having considerably high transmissivity or storativity, these recharge boundaries can halt the spread of a cone of depression by providing a source of recharge to the aquifer. They also influence the pattern of drawdown in the vicinity of pumping wells.

 

In general, the theory of well hydraulics cannot cope with the presence of one of above-mentioned aquifer boundaries. The method of images, which plays an important role in the mathematical theory of electricity, is employed in conjunction with the principle of superposition for assessing the influence of aquifer boundaries on the well flow (Ferris, 1959). This theory permits treatment of the aquifer that is limited in one or more directions. However, the additional assumption of straight-line boundaries is added, which renders aquifers of rather simple geometric form.

 

13.7.1 Image Well Theory

Boundaries are considered to be either a recharge boundary or an impermeable boundary (or a barrier boundary). A recharge boundary is a region in which the aquifer is replenished. An impermeable boundary or a barrier boundary is an edge of the aquifer where it terminates either by thinning or abutting a low-permeability formation or has been eroded away (Fetter, 1994).

 

When a pumping well is located near a recharge or barrier (impermeable) boundary, there are considerable deviations in the radial-flow pattern towards a pumping well. As a result, the solution to the flow towards wells under such conditions becomes complicated and the radial-flow equations (Theim or Theis equations) cannot be applied. For boundaries, the wells that create the same effect as a boundary are called image wells. The theory of image well was formulated (Ferris, 1959) to tackle flow problems in bounded aquifers using analytical techniques. In this theory, the effect of a recharge or leaky boundary is simulated by considering an imaginary recharging well, which is known as a ‘recharging image well’ (Fig. 13.6). Similarly, the effect of an impermeable boundary is simulated by considering an imaginary pumping well, which is known as a ‘discharging image well’ (Fig. 13.7). Thus, an image well (imaginary recharging well or imaginary pumping well) creates a hydraulic system equivalent to the effects caused by a physical boundary on the flow system. In essence, image wells enable us to transform the aquifer of finite extent to the aquifer to infinite extent. Consequently, the radial flow equations can be applied to analyze the well flow near aquifer boundaries. This is described below for the two types of aquifer boundaries.

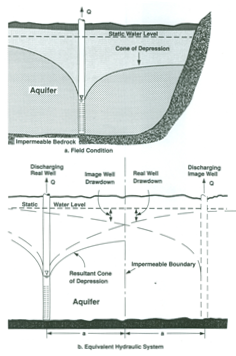
Fig. 13.6. Pumping well near a recharge boundary.

(Source: Roscoe Moss Company, 1990)

 

   

 Fig. 13.7. Pumping well near an impermeable boundary.

(Source: Roscoe Moss Company, 1990)

 

13.7.2 Pumping Near Recharge Boundary

Figure 13.6 shows a pumping well in an aquifer bounded by a recharge boundary. As the recharge boundary provides a source of recharge to the aquifer, once the cone of depression extends to the recharge boundary, it initially stops the spread of a cone of depression and then starts reducing the rate of drawdown. When the rate of recharge from the boundary becomes equal to the rate of pumping (well discharge), steady-state (equilibrium) flow condition is established in the aquifer and the drawdown becomes stationary. As mentioned above, the recharge boundary can be simulated by a recharging image well located an equivalent distance away from the recharge boundary but on the opposite side (Fig. 13.6).

 

Using the Theis equation, the unsteady drawdown in an observation well under the influence of a recharge boundary can be given as follows: 

                                                 (13.3)

 

Using the Cooper-Jacob equation (Cooper-Jacob’s approximation for the Theis well function evaluation), we have: 

                                               (13.4)

 Where, s(r,t) = drawdown in an observation well under the influence of a recharge boundary, r = distance of the observation well from the real well (i.e., pumping well), r_i = distance of the observation well from the image well (i.e., recharging image well), and the remaining symbols have the same meaning as defined earlier.  

 

If steady-state flow condition is established in the aquifer, the drawdown will stabilize and will not change with time any longer. In this case, the steady drawdown in an observation well under the influence of a recharge boundary can be given as:

                                                                         (13.5) 

If the distance between the pumping well (real well) and the recharge boundary is a and f is the angle between the line joining the real and image wells and the line joining the real well and observation well (Fig. 13.8), then Eqn. (13.5) can be expressed as: 

                                             (13.6)

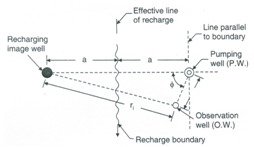
Fig. 13.8. Typical configuration of pumping well, observation well and image well in an aquifer bounded by a recharge boundary. (Source: Raghunath, 2007)

 

Moreover, the expression for steady drawdown in a pumping well (i.e., steady drawdown at the well face) under the influence of a recharge boundary can be obtained as follows by substituting r = r_w and r_i = 2a−r_w in Eqn. (13.5):

 

                                                                     (13.7)

13.7.3 Pumping Near Impermeable Boundary

Figure 13.7 shows a pumping well in an aquifer bounded by an impermeable boundary. Impermeable boundaries have the most dramatic impact on the drawdown of a pumping well for the aquifer with no source of vertical recharge. As the well withdraws water only from the aquifer storage, the drawdown continues as a function of the logarithm of time (Fetter, 1994). The impermeable boundary is simulated by a discharging image well located an equivalent distance away from the boundary but on the opposite side (Fig. 13.7). The unsteady drawdown in an observation well under the influence of an impermeable boundary can be expressed as:

 

                                                (13.8)

 

Using the Cooper-Jacob equation (Cooper-Jacob’s approximation for the Theis well function evaluation), we have:

 

                                         (13.9a)

 

Or,                                                       (13.9b)

 

Where, r_i = distance of the observation well from the image well (i.e., discharging image well), and the remaining symbols have the same meaning as defined earlier. 

 

Furthermore, the unsteady drawdown in a pumping well (i.e., unsteady drawdown at the well face) under the influence of an impermeable boundary can be expressed as:

 

                    (13.10)

 

13.7.4 Impact of Aquifer Boundaries on Time-Drawdown Curve

Figure 13.9 shows a theoretical straight-line plot of drawdown as a function of time on the semi-logarithmic paper. It is evident from this figure that the impact of a recharge boundary is to slow down (retard) the rate of drawdown. The change in drawdown can become zero if the well is supplied entirely with recharged water. In contrast, the impact of a barrier boundary or an impermeable boundary on flow in some region of the aquifer is to accelerate the drawdown rate (Fig. 13.9). In this case, the groundwater level declines faster than the theoretical drawdown curve (straight line shown in Fig. 13.9).

 

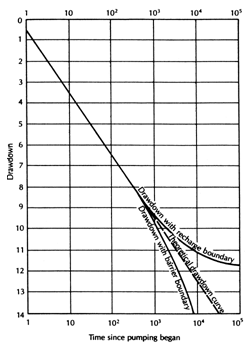
Fig. 13.9. Impact of recharge and impermeable boundaries on the time-drawdown curve. (Source: Redrawn from Fetter, 1994)

 13.8 Advantages and Disadvantages of Pumping Tests

The advantages of the pumping test method are self-evident. A pumping test provides in situ parameter values and these values are, in effect, averaged over a large and representative volume (Freeze and Cherry, 1979). From a single pumping test, one can obtain both T and S values. Also, in aquifer-aquitard systems (i.e., leaky aquifer systems), it is possible to get very important leakage properties of the system (e.g., leakage factor, hydraulic conductivity and storage coefficient of aquitards, and leakance). Moreover, the step-drawdown test provides hydraulic characteristics of production wells, including safe well yield.

 However, there are two disadvantages of the pumping test (Freeze and Cherry, 1979): one scientific and one practical. The scientific limitation is that the pumping test interpretation is not unique. For example, similarity in timedrawdown response could be found for leaky, unconfined and bounded systems. Thus, unless clear geologic evidence is available, a unique prediction of the effects of any pumping test would be difficult. The fact that a theoretical curve can be matched by the pumping test data in no way proves that the aquifer satisfies the assumptions on which the curve is based. The practical disadvantage of the method lies in its expense, including money, time and labor. Therefore, when only K or T values are required such as in the case of geotechnical and contamination studies or flownet analysis, simple and inexpensive methods like slug test should be used. These simple and cheaper methods are also useful when local conditions do not permit pumping tests or when preliminary and quick results are desired.

 

References

• Batu, V. (1998). Aquifer Hydraulics: A Comprehensive Guide to Hydrogeologic Data Analysis. John Wiley & Sons, New York.

• Ferris, J.G. (1959). Groundwater. In: C.O. Wisler and E.F. Brater (Editors), Hydrology, John Wiley and Sons, New York.

• Fetter, C.W. (1994). Applied Hydrogeology. Third Edition. Prentice Hall, NJ.

• Freeze, R.A. and Cherry, J.A. (1979). Groundwater. Prentice-Hall, New Jersey.

• Kasenow, M. (2001). Applied Groundwater Hydrology and Well Hydraulics. Second Edition, Water Resources Publications, Highlands Ranch, Colorado.

• Kruseman, G.P. and de Ridder, N.A. (1994). Analysis and Evaluation of Pumping Test Data. Second Edition, ILRI Publication 47, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands.

• Raghunath, H.M. (2007). Ground Water. New Age International (P) Limited, New Delhi.

• Roscoe Moss Company (1990). Handbook of Ground Water Development. John Wiley & Sons, New York.

• Schwartz, F.W. and Zhang, H. (2003). Fundamentals of Ground Water. John Wiley & Sons, New York.

• Todd, D.K. (1980). Groundwater Hydrology. John Wiley & Sons, New York.

 

Suggested Readings

• Raghunath, H.M. (2007). Ground Water. New Age International (P) Limited, New Delhi.

• Michael, A.M., Khepar, S.D. and Sondhi, S.K. (2008). Water Well and Pump Engineering. Second Edition, Tata McGraw Hill Education Pvt. Ltd., New Delhi.

• Sarma, P.B.S. (2009). Groundwater Development and Management. Allied Publishers Pvt. Ltd., New Delhi.

• Todd, D.K. (1980). Groundwater Hydrology. John Wiley & Sons, New York.