Theory of Machines 3(2+1)

Lesson 8.

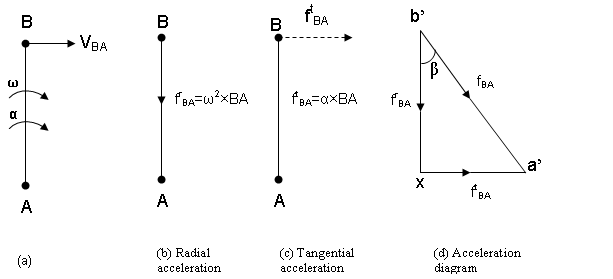
Fig. 3.16 acceleration components

8.1.1 RADIAL OR CENTRIPETAL COMPONENT OF ACCELERATION

The magnitude of radial component is given by f^r_BA= ω²×BA where f^r_BA= Radial component of acceleration of point B respect to point A (as given in fig: 3.16b). Its direction is given from B to A. When the angular velocity of a rotating link or a particle moving in a circular path is not constant, but is subjected to an angular acceleration (with consequent peripheral or linear acceleration), the resultant acceleration may be found by adding the vectors representing the centripetal and peripheral (or tangential) accelerations.  Since the centripetal acceleration is always radial and perpendicular to the instantaneous direction of the motion and the peripheral acceleration is perpendicular to the radius, these two accelerations are always mutually perpendicular and the resultant acceleration is easily found by applying the wall known relationship which exist between the sides of a right angled triangle, that is by extracting the square root of the sum of the squares of the respective accelerations.

8.1.2 TANGENTIAL COMPONENT OF ACCELERATION

It can be defined as the rate of change velocity V_BA in the tangential direction. Its magnitude will be equal to α×BA. It is represented by f^t_BA; the tangential component of acceleration of B with respect to A. f^t_BA is perpendicular to BA and parallel to V_BA.

The total acceleration of point B with respect to A is the vector sum of their components of radial and tangential acceleration. This can be written as

\[{{\text{f}}_{{\text{BA}}}}={\text{}}{{\text{f}}^{\text{r}}}_{{\text{BA}}}+{\text{}}{{\text{f}}^{\text{t}}}_{{\text{BA}}}={\text{}}{\omega ^{\text{2}}} \times {\text{BA}} + {\text{ }}\alpha\times {\text{BA}} = {\text{ }}\left( {{\omega ^{\text{2}}} + {\text{ }}\alpha } \right){\text{}} \times {\text{ BA}}\]

Here f_BA is the total acceleration of B with respect to A

8.1.3 How to draw acceleration diagram

Step 1. Draw b’x = f^r_BA in some suitable scale parallel to AB and its direction will be from B to A.

Step 2. From point x draw xa’ = f^t_BA = α×BA which is perpendicular to AB. α is known in this case.

Step 3. Join a’ with b’ which shows f_BA, which represents the total acceleration of B with respect to A. The acceleration of B relative to A is inclined at an angle of β with AB.

\[{\text{Tan }}\beta= \frac{\alpha }{{{\omega ^{\text{2}}}}}\]

When α = 0, AB rotates at the uniform angular velocity, f^t_BA = 0 and thus f^r_BA represents the total acceleration.

When ω = 0, A has a linear motion, f^r_BA = 0 and thus the tangential acceleration is the total acceleration.

 

Example: 3.3 A motor-car passes round a curve of 30.5 m radius and at a given instant has a speed of 82 km/h (or 8.89 m/s).  The car is accelerating at the rate of 16 km/h in 3 sec. find the resultant acceleration.

Sol:     

Centripetal acceleration, ƒ^r = rω² = v²/r

                                  ƒ^r   = (32000/3600)² / 30.5 =  2.59 m/s²

Tangential acceleration, ƒ^t  = (16000/3600)/3 = 1.48 m/s²

Resultant acceleration, ƒ   = √(2.59² + 1.48²) = √8.8985 = 2.983 m/s²

 

Example 3.4 The crank of a slider crank mechanism rotates a constant speed of 300 r.p.m. The crank is 150 mm and the connecting rod is 600 mm long. Determine: the angular velocity and angular acceleration of the connecting rod when the crank makes the angle of 45⁰ with form the inner dead centre.

Solution.

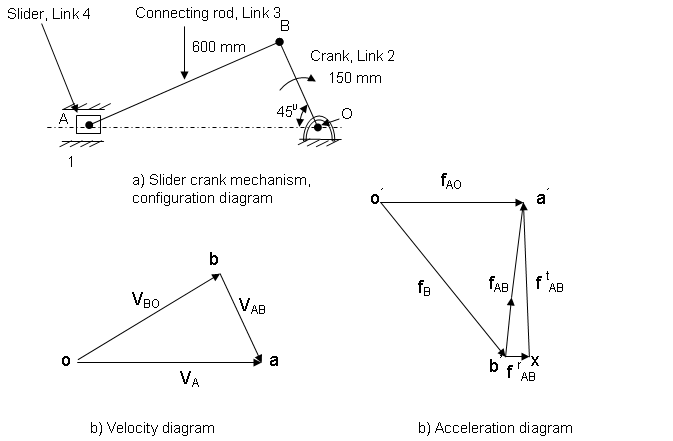
Fig. 3.17

The crank OB = 150 mm = 0.15 m

N_BO=300 r.p.m.

\[{\omega _{{\text{OB}}}} = \frac{{{\text{2}}\pi\times {\text{3}}00}}{{{\text{6}}0}} = {\text{ 31}}.{\text{4 rad}}/{\text{s}}\]

V_BO= ω _OB × OB= 31.4 × 0.15= 4.71 m/s

Velocity diagram is drawn by following these steps

Step 1. V_BO, the velocity of point B with respect to O is known and it is perpendicular to OB. Take any point o and draw vector ob which will represent V_BO.

Step 2. V_AB is perpendicular to AB, from b draw a vector ba perpendicular to AB representing V_AB.

Step 3. V_A ,the velocity of slider is along path OA. From o draw vector oa which will intersect vector ba at point a.

By measurement oa=V_A=4 m/s

                                     ba=V_AB=3.34 m/s

The radial acceleration of B with respect to O,f^r_BO is given as

\[{{\text{f}}^{\text{r}}}_{{\text{BO}}}={{\text{f}}^{\text{r}}}_{\text{B}}=\frac{{{{\text{V}}^{\text{2}}}_{{\text{BO}}}}}{{{\text{OB}}}}= \frac{{{{\left( {{\text{4}}.{\text{71}}} \right)}^{\text{2}}}}}{{0.{\text{15}}}} = {\text{147}}.{\text{8 m}}/{{\text{s}}^{\text{2}}}\]                

f^t_BO=0 as crank rotates with the constant speed

Radial acceleration of A with respect to B is given as

\[{{\text{f}}^{\text{r}}}_{{\text{AB}}}=\frac{{{{\text{V}}^{\text{2}}}_{{\text{AB}}}}}{{{\text{AB}}}}=\frac{{{{\left({{\text{3}}.{\text{34}}} \right)}^{\text{2}}}}}{{0.{\text{6}}0}} = {\text{18}}.{\text{5m}}/{{\text{s}}^{\text{2}}}\]                  

The acceleration diagram is drawn by following these steps

Step 1. Draw vector o’b’ = f^r_BO parallel to BO and 147.8 m/s² in  magnitude.

Step 2. The radial acceleration of A with respect to B, f^r_AB is known in magnitude i.e. 18.5 m/s² and parallel to AB. from b’ draw vector b’x=f^r_AB. from x draw xa’ perpendicular to b’x representing tangential component of acceleration of A with respect to B.

Step 3. The acceleration of slider A with respect to O, f_AO is along the line of stroke of OA. From o’ draw vector o’a’ representing f_AO. o’a’ intersects xa’ at point a’. Now join o’ to a’. Thus o’a’ is f_AO=f_A

By measurement f_A=o’a’= 109 m/s²

Angular velocity of the connecting rod is given by

\[{\omega _{{\text{AB}}}}=\frac{{{{\text{V}}_{{\text{AB}}}}}}{{{\text{AB}}}}= \frac{{{\text{3}}.{\text{34}}}}{{0.{\text{6}}0}} = {\text{5}}.{\text{56 rad}}/{\text{s}}\]

Angular acceleration of the connecting rod AB, α_AB is given by

\[{\alpha_{{\text{AB}}}}=\frac{{{{\text{f}}^{\text{t}}}_{{\text{AB}}}}}{{{\text{AB}}}}={\text{ }}\frac{{{\text{1}}0{\text{7}}.{\text{5}}}}{{0.{\text{6}}0}} = {\text{179}}.{\text{1 rad}}/{{\text{s}}^{\text{2}}}\]

(f^t_AB=xa’=107.5 by measurement)