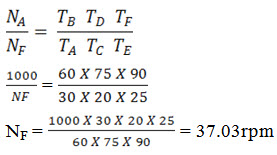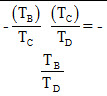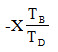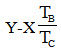Site pages
Current course
Participants
General
Module 1. Introduction to Theory of Machine
Module 2. Planar Mechanism
Module 3. Velocity and Acceleration Analysis
Topic 4
Topic 5
Topic 6
Topic 7
Topic 8
Topic 9
Topic 10
Lesson 20.
Consider epicyclic train as shown in the figure 4.13. Let TB, TC and TD be the number of teeth on sun gear N1, Planet gears N2 and internally tooth ring N3.
First suppose that spider/arm is fixed. Sun gear N1 is given +1 movement the planet gear C turns through – \[\frac{{{{\text{T}}_{\text{B}}}}}{{{{\text{T}}_{\text{C}}}}}\] and internal gear D by – \[\frac{{\left( {{{\text{T}}_{\text{B}}}} \right)}}{{{{\text{T}}_{\text{C}}}}}{\text{ }}\frac{{\left( {{{\text{T}}_{\text{C}}}} \right)}}{{{{\text{T}}_{\text{D}}}}}\] = - \[\frac{{{{\text{T}}_{\text{B}}}}}{{{{\text{T}}_{\text{D}}}}}\] Secondly when spider A is fixed, sun wheel b rotates through +X revolution and planet C will rotate through –X \[\frac{{{{\text{T}}_{\text{B}}}}}{{{{\text{T}}_{\text{C}}}}}\] and Internal Gear through –X \[\frac{{{{\text{T}}_{\text{B}}}}}{{{{\text{T}}_{\text{D}}}}}\]
Thirdly each element of an epi cyclic train is given +y revolution and finally the motion of each element is added up and entered in fourth row.
Table of Motion
|
Sr. no. |
Motion of different elements of the system |
Revolutions of different elements |
|||
|
Arm |
Sun Gear |
Planet Gear |
Ring Gear |
||
|
1 |
Spider is fixed, Sun gear rotates +1 revolution anticlockwise |
0 |
+1 |
|
|
|
2 |
Spider is fixed, sun gear rotates +X revolutions
|
0 |
+X |
|
|
|
3.
|
Add +y revolutions to every member of the system |
+Y |
+Y |
+Y |
+Y
|
|
4. |
Motion of individual members of the system |
+Y |
X+Y |
|
|
Q1. The compound gear train is as shown in the figure 4.14. The power shaft is connected to gear A having 30 teeth and rotates at 1000rpm. The spur gears B, C, D and E have 60, 20, 75 and 25 teeth respectively. Calculate the rpm of gear F if it has 90 teeth.
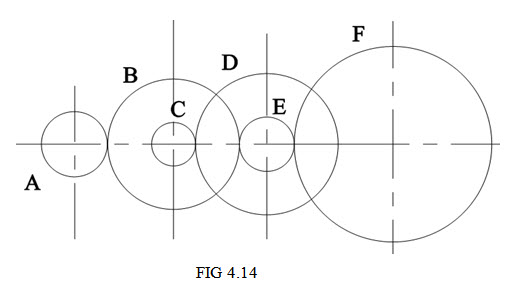 Sol:- let NF = speed of gear F
Sol:- let NF = speed of gear F
TA = 30
TB = 60
TC =20
TD = 75
TE =25
TF = 90