Heat and Mass Transfer 2(2+0)

Lesson 19. Emission of Radiation

Black Body:

A perfect black body is one that absorbs all the thermal radiation, irrespective of wavelength, received by it. It does not reflect or transmit incident thermal radiation; therefore, absorptivity of such a body is 100%. At a given temperature and wavelength, a black body emits more energy as compared to any other body.

A perfect black body is a hypothetical body which behaves like a perfect absorber and emitter of thermal radiation and in practice no substance or body possesses properties of a perfect black body. However, bodies showing close approximation to a perfectly black body can be constructed.

Consider a hollow sphere with inside surface blackened and having a small hole at its surface. Thermal radiations entering the sphere through the hole are reflected repeatedly by the inner walls till they are completely absorbed. To avoid a direct reflection from inner surface, a pointed projection is made inside the sphere facing the hole as shown in Figure 1. Therefore, the small hole acts as a black body absorber. 

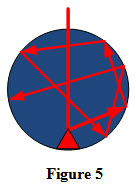
In order to compare radiative properties of real surfaces, a hypothetical body called blackbody is defined. A blackbody is an hypothetical body and has following properties.

• A black body absorbs all incident radiation irrespective of their wavelength and direction.

• At a given temperature and wavelength, energy emitted by a black body is the highest as compared to any other body.

• The radiation emitted by a black body depends upon wavelength and temperature, but it is independent of direction. 

Monochromatic emissive power (E_bλ) and Planck’s Law:

Monochromatic emissive power is defined as the energy emitted by a black body at a given wavelength in all directions per unit area per unit time and it is expressed in the units as W/(m²- µm). Using his quantum theory, Max Planck derived the expression for monochromatic emissive power (E_bλ) which is expressed as

\[{{\text{E}}_{{\text{b}}\lambda }} = \frac{{2\pi {c^2}h\,{\lambda ^{ - 5}}}}{{\left( {\exp \frac{{ch}}{{\lambda kT}}} \right) - 1}}\]         (1)

Where

           c – Velocity of light

              = 2.98 Ҳ 10⁸ m/sec

           h – Planck’s constant

              = 6.625 Ҳ 10^-34 Joule-Sec

           k – Boltzmann constant      

              =  1.3805 Ҳ 10^-23 Joule/K

           λ – Wavelength monochromatic radiation emitted, m

           T – Absolute temperature, K

Equation (1) can also be expressed as 

\[{{\text{E}}_{{\text{b}}\lambda }} = \frac{{{C_1}\,{\lambda ^{ - 5}}}}{{\left( {\exp \frac{{{C_2}}}{{\lambda kT}}} \right) - 1}}\]         (2)

Where

C₁ = 2πc²h = 37.404 Ҳ 10^-17 J-m²/K

C₂ = ch/k = 1.4387 Ҳ 10^-2 m – K

Equation (2) is known as Planck’s law or Planck’s distribution.

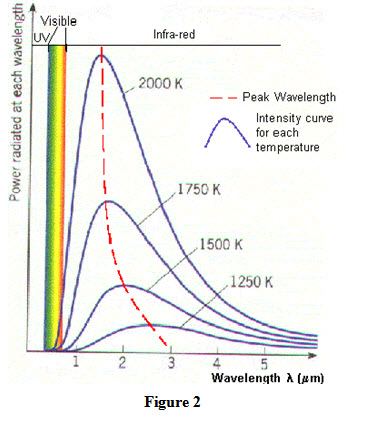
Monochromatic emissive power of a black body is a function of wave length and its variation with wavelength at selected temperatures has been plotted as shown in Figure 2. Following observations have made from this plot:

• At a specified temperature, monochromatic emissive power increases with increase in wavelength and attains a maximum value corresponding to a particular wavelength. However, further increase in wavelength results in decrease in emissive power.

• With increase in temperature, emissive power increases for all wavelengths.

• An increase in temperature results in decreases in value of wavelength for which emissive power is maximum.

• Area under each curve represents energy emitted by the black body at a particular temperature for the range of wavelength considered. With increase in temperature area under the curve increases as energy emitted increases.

  

Problem 7.7   A furnace inside temperature of 2250 K has a glass circular viewing of 6 cm diameter. If the transmissivity of glass is 0.08, make calculations for the heat loss from the glass window due to radiation.

Solution:    The radiation heat loss from the glass window is given by

                                                       

Where \[\tau \] is the transmissivity of glass

Problem 7.4    A thin metal plate of 4 cm diameter is suspended in atmospheric air whose temperature is 290 K. the plate attains a temperature of 295 K when one of its face receives radiant energy from a heat source at the rate of 2 W. If heat transfer coefficient on both surfaces of the plate is stated to be 87.5 W/m²-deg, workout the reflectivity of the plates.

Solution:   Heat lost by convection from both sides of the plate

                    = 2h A Δt

The factors 2 accounts for two sides of the plate

For most of solids, the transmissivity is zero.

Energy lost by reflection = 2.0-1.1 =0.9 W

Reflectivity     

 

Problem 7.9    A black body of total area 0.045 m² is completely enclosed in a space bounded by 5 cm thick walls. The walls have a surface area 0.5 m² and thermal conductivity 1.07 W/m-deg. If the inner surface of the enveloping wall is to be maintained at 215°C and the outer wall surface is at 30°C, calculate the temperature of the black body. Neglect the difference between inner and outer surfaces areas of enveloping material.

Solution:   Net heat radiated by the black body to the enclosing wall,

Where T_b  is the temperature of the black body in degree kelvin.

Heat conducted through the wall,

Under steady state conditions, the heat conducted through the wall must equal the net radiation loss from the black body. Thus

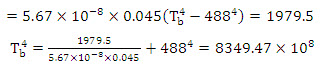
Temperature of the black body, T_b =955.9 K

Problem 7.12  A furnace radiation at 2000K. Treating it as a black body radiation, calculate the

(i) Monochromatic radiant flux density at 1 μm wavelength.

(ii) Wavelength at which emission is maximum and the corresponding radiant flux density

(iii) Total emissive power, and

(iv) Wavelength λ such that emission from 0 to λ is equal to the emission from λ to ∞.

Solution:   (a) From Planck’s law of distribution,

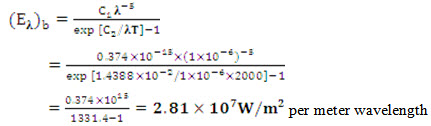
(b) From Wien’s displacement law;  

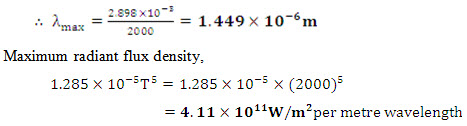
(c) From Stefan – Boltzman law,

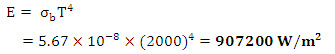
(d) The emission in the band width 0 to λ is half of the total emission from 0 to ∞. Therefore, fractional emissive power is 0.5. Corresponding to F_0-λ = 0.5, the wavelength temperature product as read from table 7.1 is approximately 4100 μm-K. Thus λT = 4100 and so

Problem 7.16  A polished metal pipe 5 cm outside diameter and 370 K temperature at the outer surface is exposed to ambient conditions at 295 K temperature. The emissivity of the surface is 0.2 and the convection coefficient of heat transfer is 11.35 W/m²-deg. Calculate the heat transfer by radiation and natural convection per metre length of the pipe. Take thermal radiation constant   What would be the overall coefficient of heat transfer by the combined mode of convection and radiation?

Solution:

 

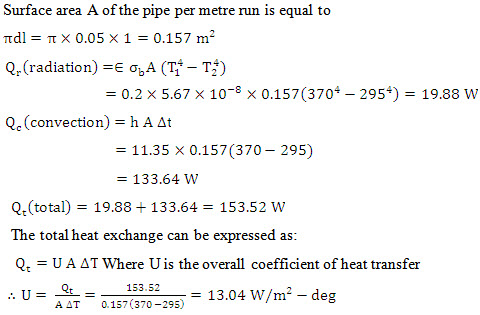
Problem 7.18  A gray surface has an emissivity  at a temperature of 550 K source. If the surface is opaque, calculate its reflectivity for a black body radiation coming from a 550 K source.

(b) A small 25 mm square hole is made in the thin-walled door of a furnace whose inside walls are at 920 K. if the emissivity of the walls is 0.72, calculate the rate at which radiant energy escapes from the furnace through the hole to the room.

Solution:     The requirement that all of the radiant energy striking any surface may be accounted for is:

Note: The data about the emissivity of the inside wall is not needed.