Heat and Mass Transfer 2(2+0)

Lesson 20. Stefan-Boltzman Law

The equation obtained on the basis of experimental work and proved theoretically was called as Stefan-Boltzman law which states that total energy emitted by a black body per unit area and per unit time is directly proportional to the fourth power of its absolute temperature and is expressed as:

                                  E_b = σ_b T⁴                                                                               (1)

E_b -  Energy emitted from a black body per unit area per unit time, W/m²

σ_b – Stefan-Boltzman constant

      = 5.678 x 10^-8  W/(m²-K⁴)

T - Absolute temperature of the emitting surface, K.

Equation (1) represents energy emitted in the form of heat by a black body at a given temperature irrespective of heat that it has received from surroundings. A black body at temperature T₁, surrounded by another black body at temperature T₂ is emitting thermal radiation and at the same time receiving thermal radiation form the surrounding body, therefore, net energy per unit time lost by it is expressed as

\[{E_{net}} = {\sigma _b}\left( {T_1^4\, - \,T_2^4} \right)\]        (2)

 Emissivity, ε

Emissivity is a property of a body which is defined as the ratio of emissive power of the body to the emissive power of a hypothetical black body when both the bodies are maintained at same temperature.

\[{\mathbf{\varepsilon }} = \,\frac{E}{{{E_b}}}\]         (3)

Depending upon the direction of emission of energy, emissivity can be categorized as

i) Monochromatic emissivity: It is the ratio of monochromatic emissive power of a body to the monochromatic emissive power of a black body at same wave length and temperature.

\[{{\mathbf{\varepsilon }}_\lambda } = \,\frac{{\left( {{E_\lambda }} \right)}}{{{{\left( {{E_\lambda }} \right)}_b}}}\]     (4)     

ii) Total emissivity: It is the ratio of the total emissive power of a body to the total emissive power of a black body maintained at same temperature.

\[{\mathbf{\varepsilon }} = \,\frac{E}{{{E_b}}}\]      (5)

iii) Normal total emissivity: It is the ratio of the normal component of total emissive power of a body to the normal component of total emissive power of a black body maintained at same temperature.

\[{{\mathbf{\varepsilon }}_n} = \,\frac{{{E_n}}}{{{{\left( {{E_b}} \right)}_n}}}\]          (6)

Kirchoff’s Law of Radiation

According to Kirchoff’s Law ratio of total emissive power to absorptivity is constant for all bodies which are in thermal equilibrium with their surroundings. For three bodies in thermal equilibrium with each other, it can be written

\[\frac{{{E_1}}}{{{\alpha _1}}} = \,\frac{{{E_2}}}{{{\alpha _2}}} = \frac{{{E_3}}}{{{\alpha _3}}} = Cons\tan t\]            (7)

Assuming third body to be black body, equation (7) can be written as

\[\frac{{{E_1}}}{{{\alpha _1}}} = \,\frac{{{E_2}}}{{{\alpha _2}}} = \frac{{{E_b}}}{{{\alpha _b}}} = Cons\tan t\]      (8)

Since for a black body, \[{\alpha _b}\] =1, equation (8) can be written as

\[\frac{{{E_1}}}{{{\alpha _1}}} = \,\frac{{{E_2}}}{{{\alpha _2}}} = {E_b}\]           (9)

\[\frac{{{E_1}}}{{{E_b}}} = \,{\alpha _1}\,,\,\,\,\,\frac{{{E_2}}}{{{E_b}}} = {\alpha _2}\]           (10)

However, according to definition of emissivity,

\[\frac{{{E_1}}}{{{E_b}}} = \,{\varepsilon _1}\,,\,\,\,\,\frac{{{E_2}}}{{{E_b}}} = {\varepsilon _2}\]         (11)

Comparing equations (10) and (11), we can write

\[{\varepsilon _1} = \,{\alpha _1}\,,\,\,\,\,{\varepsilon _2} = {\alpha _2}\]                 

Or     \[\varepsilon= \,\alpha \]     (12)

Therefore, Kirchoff’s law states that for a body in thermal equilibrium with its surroundings, its absorptivity is equal to its emissivity.

Gray body and its emissive power:

For a given temperature absorptivity and emissivity of a black surface are equal and it emits more energy as compared to a real surface. Emissivity and absorptivity of a real surface ma vary with temperature or wavelength of radiations emitted or absorbed. However for a gray body emissivity and absorptivity are independent of wavelength. A gray body is defined as a surface whose emissivity is constant at all temperatures and throughout the entire range of wavelength. Therefore, a gray body, like black body, is an ideal body and values of its absorptivity and emissivity are less than unity. Emissivity of a gray body is expressed as

\[\varepsilon= \,\frac{{Energy\,emitted\,by\,\,a\,gray\,body\,at\,temperature\,'T'}}{{Energy\,emitted\,by\,\,a\,black\,body\,at\,temperature\,'T'}} = \frac{E}{{{E_b}}}\]                      

\[\varepsilon \, = \,\frac{{\sigma {{\text{T}}^{\text{4}}}}}{{{\sigma _{\text{b}}}{{\text{T}}^{\text{4}}}}} = \frac{\sigma }{{{\sigma _{\text{b}}}}}\]                                               

Value of Stefan-Boltzman’s ‘σ’ constant depends upon nature of body, state of its surface and temperature. For a black body value of Stefan-Boltzman’s ‘σ’ is equal to 5.67 Ҳ 10^-8 W/ m²-K⁴.

Wien’s Displacement Law:

Wein’s displacement law states that product of absolute temperature and wavelength at which emissive power is maximum, is constant. It has been established that monochromatic emissive power of a black body depends upon its temperature and wavelength of emitted radiations. For a given temperature, emissive power initially increases with increase in wavelength, attains a maximum value corresponding to   particular wavelength and then decreases with further increases in wavelength of emitted radiations as discussed in the previous Lesson. With increase in temperature, maximum emissive power occurs at smaller wavelengths. Wein’s displacement law gives the value of the wavelength at which emissive power of a body is maximum for a given temperature and is expressed as

\[{(\lambda )_m}\,T = \,0.0029\,\,\,\,m - K\] 

\[{(\lambda )_m}\] - Wavelength at which monochromatic power is maximum corresponding to temperature ‘T’.

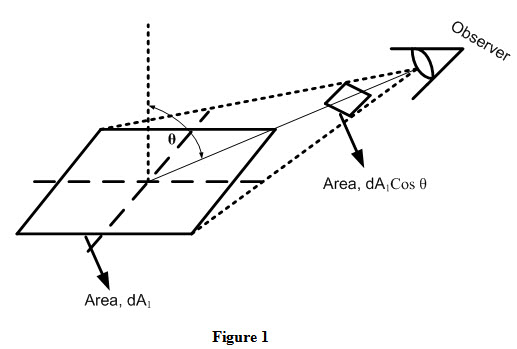
Projected Area

The area, dA₁, as seen from the prospective of a viewer, situated at an angle θ from the normal to the surface, will appear somewhat smaller, as cos θ·dA₁. This smaller area is termed the projected area and has been shown in Figure 1.