Site pages
Current course
Participants
General
Module 1. Basic Concepts, Conductive Heat Transfer...
Module 2. Convection
Module 3. Radiation
Module 4. Heat Exchangers
Module 5. Mass Transfer
Lesson-21 Solid Angle and Intensity of Radiation, Radiation Heat Transfer between Two Black Bodies
Unit Solid Angle and Intensity of radiation:
Generally speaking solid angle is that fraction of surface of a sphere that is seen by an observer positioned at the centre of a sphere. The ratio of area of this small surface being observed from centre of the sphere to square of radius of sphere represents solid angle. An observer standing at the centre of a sphere of radius ‘R’ will see a curve (which is fraction of surface of sphere)
The unit solid angle is defined as the angle covered by unit area on a surface of a sphere of unit radius when joined with the centre of the sphere and has been shown in Figure 1. Unit solid angle is measured in the steradians and is expressed as

The intensity of radiation is defined as the rate of emission of radiation in a given direction from a surface per unit solid angle and per unit projected area of a radiating surface on a plane perpendicular to the direction of radiation.
Eb = π Ib
Eb is the energy emitted and Ib is the intensity of radiations.
Radiation Heat Transfer between Two Black Bodies: Configuration Factor
Radiation heat exchange between two bodies is influenced by the following parameters
i) Temperature of the individual bodies
ii) Radiation properties of the individual bodies such as emissivity
iii) Orientation of the bodies relative to each other
Orientation of bodies relative to each other means how well one body is able to see the other body. The effect of orientation of the bodies on radiation heat transfer is accounted by considering a factor called configuration factor which is also called shape or view factor. In order to understand the significance of configuration factor let us consider a body 1 which emitting radiations from its bottom surface only and a part of these radiations is intercepted by each of three bodies 2,3 and 4 as shown in Figure 2.
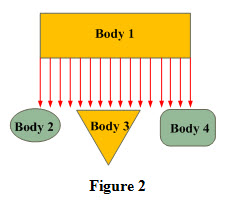
Configuration factor between body 1 and body 2 is denoted by F1-2 and is expressed as
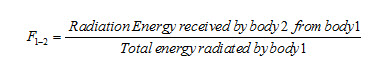
Subscript 1 represents the emitting body and 2 represents the receiving or intercepting body.
Similarly, configuration or view or shape factor between body 2 and body 1 can be expressed as
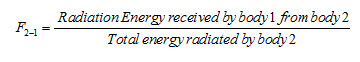
Similarly, configuration or view or shape factor between body 1 and body 3 can be expressed as
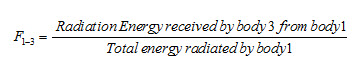
Similarly, configuration or view or shape factor between body 1 and body 4 can be expressed as
![]()
Configuration or view or shape factor depends upon the geometry / shape of the bodies involved in the radiation heat exchange and is independent of surface properties and temperatures of the bodies.
A mathematical expression for configuration or view or shape factor can be obtained by considering two black bodies 1 and 2 exchanging heat by radiations when maintained at temperatures T1 and T2 respectively. These two bodies are at a distance ‘S’ from each other and having areas A1 and A2 respectively as shown in Figure 3.
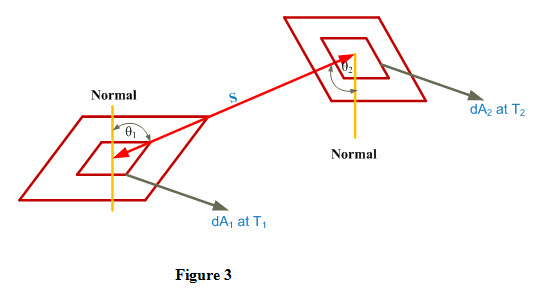
Let us consider two small elements of areas dA1 and dA2 at the centers of black bodies 1 and 2 respectively which are exchanging heat with each other by radiation.Heat radiated from element of area dA1 towards element of area dA2 is expressed as dQ(1-2) = Intensity of radiation of element of area dA1 Ҳ projected area of element of area dA1 along OP Ҳ solid angle made by element of area dA2
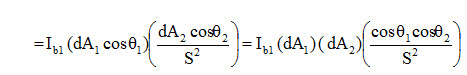
This is the total heat lost by the element of area dA1 and received by the element of area dA2. Similarly heat is radiated by the element of area dA2 which is at lower temperature (T2 < T1) and received by the element of area dAl is expressed as
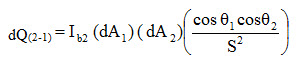
:. Net heat radiated by the element of area dA1 towards the element of area dA2
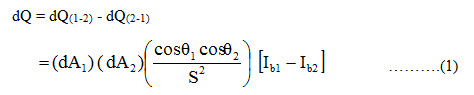
Since intensity of radiation is given by
Ib = Eb/ п = (σ T4)/ п
Therefore, Ib1 = Eb1/ п = (σ T14)/ п and Ib2 = Eb2/ п = (σ T24)/ п
Substituting the values of Ib1 and Ib2 in equation (1)
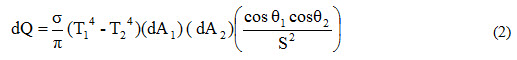
In order to determine the total energy radiated from body 1 towards body 2, equation (2) is integrated over areas A1 and A2.

where is total heat radiated from body 1 towards body 2
or Net = F(1-2) A1σ (T14 – T24) (4)
Comparing equations (3) and (4), we get
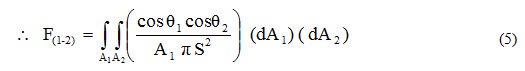
where F(1-2) is called the configuration factor or shape factor or view factor between the two radiating bodies and is a function of geometry only.
The subscripts 1 and 2 signify that the configuration factor is from body 1 to body 2. The configuration factor from body 2 to body 1 is given by
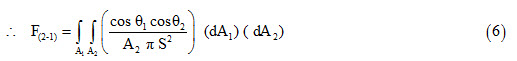
The net energy lost by body 1 must be equal to net energy gained by body 2.
:. Q(1-2) = - Q(2-1) ( As T2 < T1, so -ve sign )
:. F(1-2) A1σ (T14 – T24) = - F(2-1) A2σ (T24 – T14)
:. F(1-2) A1 = F(2-1) A2 (7)
Equation (9) is known as reciprocal relation between the shape factors.
If Area A1 is small compared with A2, then
