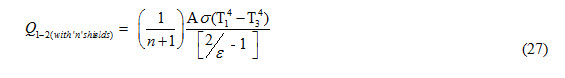Heat and Mass Transfer 2(2+0)

Lesson-23 Radiation between two infinite parallel plates and proof of Kirchhoff’s law of Radiation, Radiation Shield

Therefore        E = αE_b

But the ratio of total emissive power of any body to the total emissive power of a black body at the same temperature is called the emissivity of the body and is numerically equal to absorptivity.

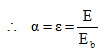
Consider two bodies C and D whose absorptivity are α_c and α_d as shown in Figure 1.

Considering the energy emitted by the body D.

(1) D emits the energy = E_d                                                                                                 (1)

(2) C absorbs energy = E_d. α_c                                                                                               (2)

     and reflects energy=E_d (1 - α_c)                                                                                        (3)

(3) D absorbs energy = E_d α_d (1 - α_c)                                                                                   (4)

      and reflects energy = E_d (1 - α_d) (1 - α_c)                                                                         (5)

(4) C absorbs energy  = E_d α_c (1 - α_c)  (1 - α_d)                                                                      (6)

      and reflects energy = E_d  (1 - α_c)²  (1 - α_d)                                                                       (7)

(5) D absorbs energy  = E_d. α_d (1 - α_c)²  (1 - α_d)                                                                    (8)

      and reflects energy = E_d  (1 - α_c)²  (1 - α_d)²                                                                      (9)

and so on upto  times.

Considering the energy emitted by the body C.

(1) C emits the energy = E_c                                                                                                    (10)

(2) D absorbs energy = E_c. α_d                                                                                                 (11)

     and reflects energy=E_c (1 – α_d)                                                                                          (12)

(3) C absorbs energy = E_c α_c (1 – α_d)                                                                                      (13)

      and reflects energy = E_c (1 – α_c) (1 – α_d)                                                                           (14)

(4) D absorbs energy  = E_c α_d (1 – α_d)  (1 – α_c)                                                                        (15)

      and reflects energy = E_c  (1 – α_d)²  (1 – α_c)                                                                         (16)

(5) C absorbs energy  = E_c. α_c (1 – α_d)²  (1 – α_c)                                                                       (17)

      and reflects energy = E_c  (1 – α_d)²  (1 – α_c)²                                                                        (18)

and so on upto infinite number of  times.

Considering equations (1), (4), (8), (11), (I5),   net energy lost by the body D

         = Energy emittedby it – energy absorbedby it

q_(dc) =E_d – [E_d α_d (1 - α_c) + E_d. α_d (1 - α_c)²  (1 - α_d) + ….] – [E_c. α_d + E_c α_d (1 – α_d)  (1 – α_c) +….]

Assuming   (1 - α_c) (1 – α_d) = K

 q_(dc)  = E_d – E_d α_d (1 - α_c) [1 + K + K²  + …...] – E_c. α_d [1 + K + K²  + ….]

But   1 + K + K²  + …... = (1 –K)^-1

 q_(dc) = E_d – (1 –K)^-1 [E_d α_d (1 - α_c) + E_c. α_d ]

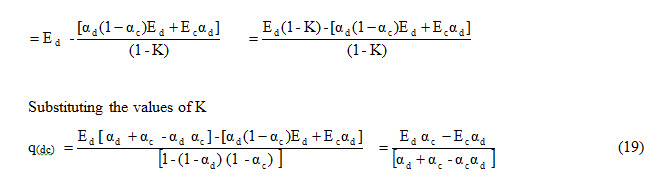
i) If originally both bodies are at same temperature

Then     q_(dc)  = 0          from equation (18A)

E_d a_c = E_c a_d

Assuming C as black body     

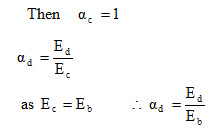
Subscription ‘b’ represents black body.

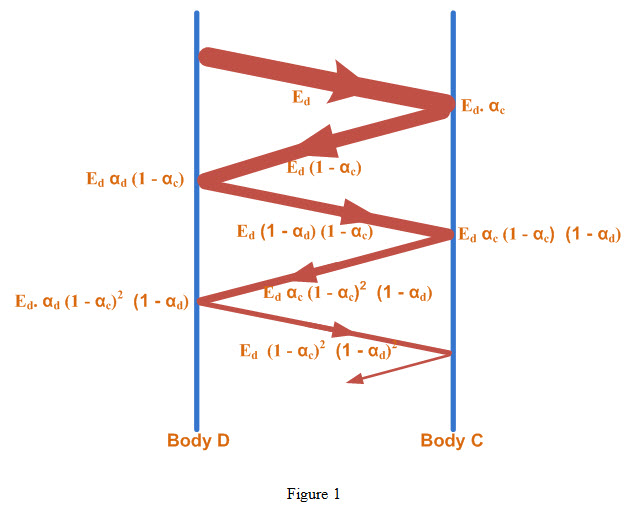
However, E_d / E_b is the emissivity of body ‘D’ according to definition of emissivity.                

ε_d = α_c This is the statement of Kirchoff’s law and hence it is proved.

ii) If both the bodies are at different temperatures

Using equation (19)

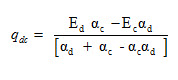
According to Stefan-Boltzman Law

E_d = ε_d σ_b T₁⁴

E_c = ε_c  σ_b T₂⁴

Substituting these values in equation (19), we get

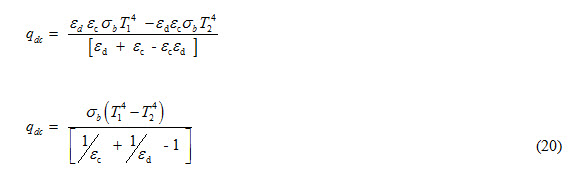
Radiation Shields

Generally, the shields are used for reducing the heat radiation from one plane to another plane. If the shield 3 is placed in between the two planes as shown in Figure 2 and considering they are at temperatures T₁, T₂ and T₃.

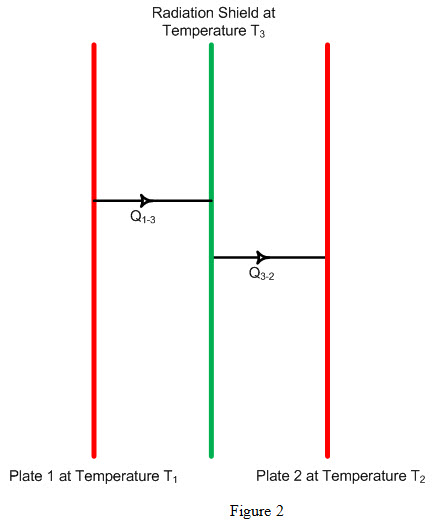
Assuming there is no temperature drop in the shield and considering the system is in steady state condition, we can write down the heat flow equation as

 

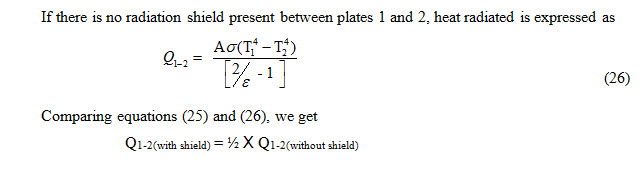
It means that with the addition of radiation shield, heat transfer rate is reduced to half of that of without the presence of radiation shield between two parallel bodies exchanging heat with each other by radiation. If ‘n’shields are present between the two radiating bodies, then the heat transfer will be expressed as