Lesson22 Shape factor and its properties, Shape Factor of a Cavity with itself, Shape Factors of complex configurations derivable from perpendicular rectangles with common edge

Properties of Configuration Factor:

Properties of shape factor are as:

1. The shape factor is purely a function of geometrical parameters.

2. When two bodies radiating energy with each other only, the shape factor relation is expressed as A1 F1-2 = A2 F2-1                                                                                       (1)

3. The shape factor of convex surface or flat surface with the other surface enclosing the first is always unity. This is because all the radiation coming out from the convex surface is intercepted by the enclosing surface but not vice versa.

4. A concave surface has a shape factor with itself because the radiation energy coming out from one part of the surface is intercepted by another part of the same surface. The shape factor of a surface with respect to itself is denoted by F1-1.

                              F1-1 = 0   for convex and flat surface.

If a surface of area Al is completely enclosed by a second surface of area A2 and if Al does not see itself  (F1-1 = 0)  then F1-2 = l  

Then substituting the value of F1-2 = l   in equation (1) ,

e22.1

Radiant exchange between coaxial cylinders, bodies placed in enclosures (sphere is kept in a room or box) are examples of this situation.

5. If n surfaces are taking part in radiation heat transfer then the energy radiated by one is always intercepted by the remaining (n-l) surfaces and by the surface itself also

               F1-1 + F1-2 + F1-3  ……………F1-n = 1

               F2-1 + F2-2 + F2-3  ……………F2-n = 1                                                                    (2)

               :          :                                     :

               :          :                                     :

               Fn-1 + Fn-2 + Fn-3  ……………Fn-n = 1

In addition to the above equations, the reciprocal relation between any two surfaces also holds good

                          F(1-2) A1 =  F(2-1) A2                   or            F(1-3) A1 =  F(3-1) A3     and so on.   

6. The shape factor between the surfaces Al and A2 is equal to the sum of the shape factors between the surface A2 and the surfaces which make the surface A1, This point is illustrated as shown in Figure 1.


f22.1                         

This states that the amount of radiated energy by A2 and intercepted by A1 is equal to the sum of the radiated energy intercepted by the areas A3 and A4 as shown in Figure.

Consider two surfaces of areas Al and A2 are radiating heat to each other as shown in Figure1. Let A1 be subdivided into A3 and A4 (i.e. A1 =A3+A4).

Then the radiant heat exchange between A1 and A2 is expressible as

                        Q1-2 = Q3-2 + Q4-2

Considering the surfaces black

                        F(1-2) A1σ (T14 – T24) =  F(3-2) A3σ (T34 – T24) + F(4-2) A4σ (T44 – T24)

             As T3 = T4 = T1 and A3 and A4 are merely sub-divisions of A1

Therefore    F(1-2) A1=  F(3-2) A3 + F(4-2) A4                                                                                                                     (3)

The above expression shows that

             F1-2    (F3-2 + F4-2 )            

For radiant exchange from A2 to A1 (divided into A3 and A4) one has      

                              F(2-1) A2=  F(2-3) A2 + F(2-4) A2

 Therefore                 F(2-1) =  F(2-3) + F(2-4)                                                                                (4)

7. If  the interior surface of a completely enclosed space such as room is subdivided into n parts, each part having a finite area A1, A2, A3, A4,…………An, then

               F1-1 + F1-2 + F1-3  ……………F1-n = 1

               F2-1 + F2-2 + F2-3  ……………F2-n = 1

               :          :                                     :

               :          :                                     :

               Fn-1 + Fn-2 + Fn-3  ……………Fn-n = 1

e22.2

The above representation admits the shape factors F1-1, F2-2, F3-3,……………. Fn-n , since some of the surface may see themselves if they are concave.

Shape Factor of a Cavity with itself:

Figure 2 shows an irregular cavity having an inner area A1 and is covered by a flat surface of area A2. Configuration factor equations for this arrangement is written as

f22.2

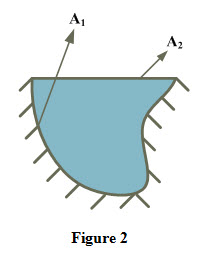
                  F1-1+F1-2= 1                                                                                                         (6)  

                  F2-2 + F2-1=1                                                                                                         (7)

Since the cavity is covered by a flat surface, so F2-2 = 0,

Substituting the value of F2-2 = 0 in equation (7), we get

                 F2-1 = 1                                                                                                                   (8)

The reciprocal relation between two surfaces is expressed as

                  F1-2 A1 =  F(2-1) A2

Using equation (8), the reciprocal relation can be written as

                  F1-2 =   A2 / A1                                                                                                       (9)

Substituting the values of F1-2 in equation (1),

e22.3

Equation (10) represents configuration factor of a cavity with itself.

e22.4

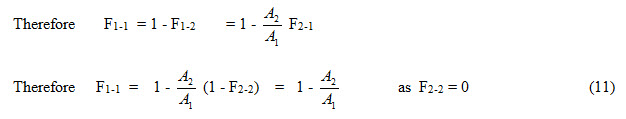
The above expression is valid for all types of the cavities as shown in Figures 3 (a), (b), and (c).

f22.3

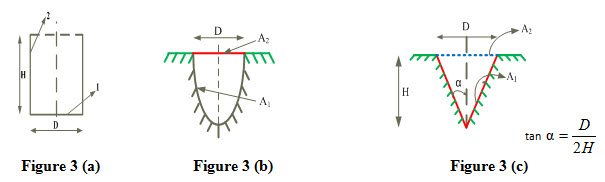
(a)  Shape factor of a cylindrical cavity of diameter D and height H with itself

e22.5

From Figure 3 (a), it can be written that

e22.6

Substituting the values of A1 and A2 in equation (12)

e22.7                      

(b) Shape factor of a hemi-spherical cavity of diameter D with itself

From Figure (b), it can be written that

e22.8

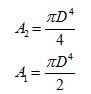
Substituting the values of A1 and A2 in equation (12)

e22.9   

(c) Shape factor of a conical cavity of diameter D and height H with itself

 From Figure 3(c), it can be written that

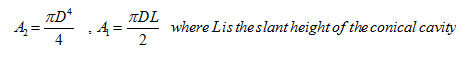
e22.10

Substituting the values of A1 and A2 in equation  (12)

e22.11

Shape Factors for Two Prependicular Plates:

Determination of configuration factor for commonly used geometries such as parallel and perpendicular walls, parallel disks is cumbersome and complicated, therefore in such cases configuration factor is determined with the help of graphs.

Shape factors for a system of Two Prependicular Plates

f22.4

Figure 2  Configuration Factor for two perpendicular plates 

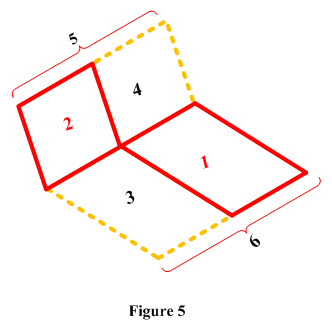
Complex Configurations Derivable From Perpendicular Rectangles with Common Edge:

i) One rectangle is displaced from the common intersection line

 A1 F1-4 = A1 F1-3+A1 F1-2

Therefore    F1-2 = F1-4 – F1-3                                                                                  (16)

The shape factors F1-3 and F1-4 may be found easily from the graph as shown in Figure 2.

F22.5

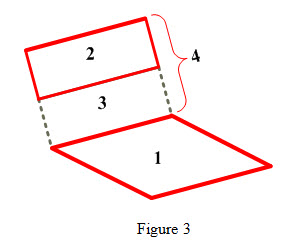
ii) Both rectangles are displaced from the common intersection line. 

A1 F1-2 = A5 F5-2 - A3 F3-2

        = (A5 F5-6 – A5 F5-4) – (A3 F3-6 - A3 F3-4)

       = (A5 F5-6 – A5 F5-4 – A3 F3-6 + A3 F3-4)

       = (A5 F5-6 + A3 F3-4) – (A5 F5-4 + A3 F3-6)                                                                17

The shape factors F5-6, F3-4,  F5-4 and   F3-6    may be found from graph as shown in Figure 2.   

 F1-2 = 1/A1 [(A5 F5-6 + A3 F3-4) – (A5 F5-4 + A3 F3-6)]     

F22.6

iii) The corner of both rectangles are touching at a point which lies on common intersection line. 

                  A1 F1-2 = A6 F6-5 – A1 F1-4 – A3 F3-2 – A3 F3-4                                                                      (18)

The following reciprocal relation is valid for the above configuration.

                A1 F1-2 = A3 F3-4

Substituting this in the above equation (18)

    F1-2 = 1/A1 [A6 F6-5 – A1 F1-4 – A3 F3-2 ]                                                                         (19)

The shape factors F6-5, F1-4,   and   F3-2    may be found from graph as shown in Figure 2.

F22.7

Last modified: Monday, 24 March 2014, 5:05 AM